【计算几何】叉积

news2025/1/14 18:29:30

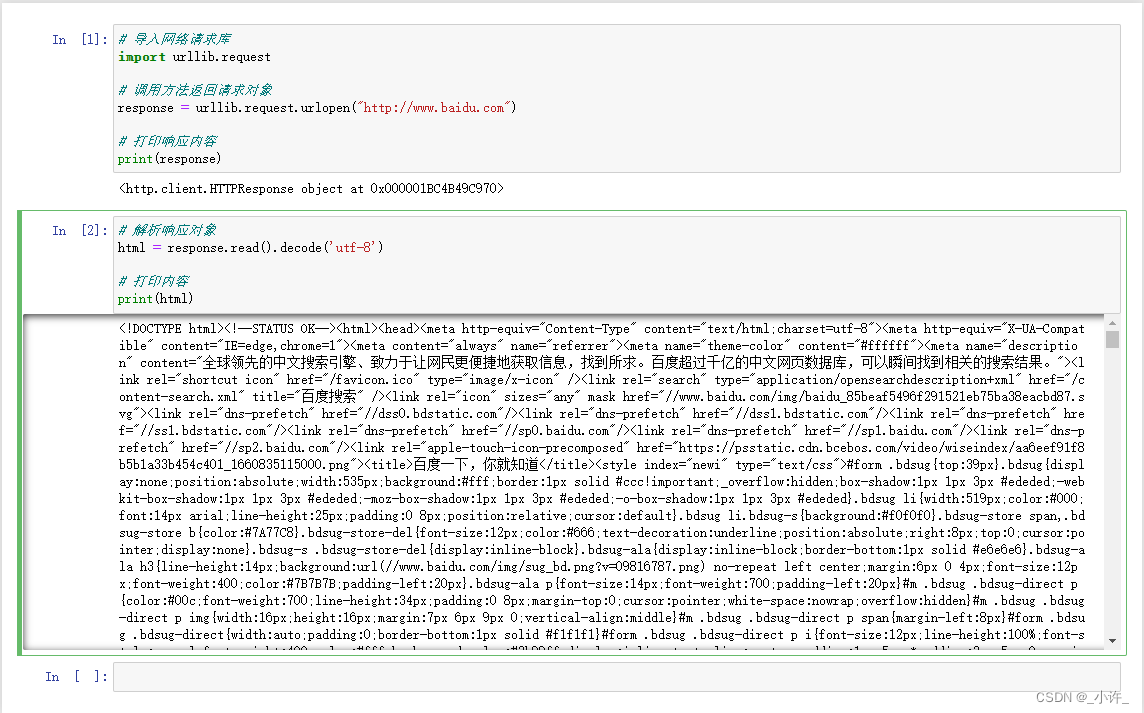
叉积

海伦公式求三角形面积

已知三角形三条边分别为a，b，c,设 $=\frac{a+b+c}{2}$ ,
那么三角形的面积为：
$\sqrt{p(p-a)(p-b)(p-c)}$
缺点：在开根号的过程中精度损失

概念

两个向量的乘积，设有p1，p2两个坐标，p1表示从（0,0）点出发，到（x1，y1）的坐标，p2表示从（0,0）点出发，到（x2，y2）的坐标。
计算公式：
$p1\times p2=\begin{pmatrix} x1 &x2 \\ y1 &y2 \end{pmatrix}$
=x1y2-x2y1
=-p2×p1（不满足交换律）

设p0p1和p0p2是任意向量，已知三个p点的坐标，要求他们的叉积
p0p1向量的坐标是（x1-x0，y1-y0）
p0p2向量的坐标是（x2-x0，y2-y0）
再对这两个向量求叉积就行了：
$\begin{pmatrix} x1-x0 &x2-x0 \\ y1-y0 &y2-y0 \end{pmatrix}$
结果是：
（x1-x0）（y2-y0）-（x2-x0）（y1-y0）

方向：
如果p1×p2>0，p1在p2顺时针方向上
如果p1×p2=0，p1和p2共线
如果p1×p2<0，p1在p2的逆时针方向

用叉积判断两个向量的位置关系

1.给定具有共同端点的两个有向线段 $\overrightarrow{p_0p_1}$ 和 $\overrightarrow{p_1p_2}$ ，请问 $\overrightarrow{p_0p_1}$ 是否在 $\overrightarrow{p_0p_2}$ 的瞬时针方向上？
2.给定两个有向线段 $\overrightarrow{p_0p_1}$ 和 $\overrightarrow{p_1p_2}$ ，如果我们首先沿着p0p1的方向走，然后沿着p1p2走，请问在p1点，是左转还是右转？
3.给定两个向量 $\overrightarrow{p_1p_2}$ 和 $\overrightarrow{p_3p_4}$ ，如何判断他们是否相交？

(1)用向量 $\overrightarrow{p_0p_1}$ × $\overrightarrow{p_0p_2}$ ，如果>0就在顺时针方向上
(2)构造 $\overrightarrow{p_0p_2}$ 这个向量，如果 $\overrightarrow{p_0p_1}$ × $\overrightarrow{p_0p_2}$ >0说明是向左，否则向右
(3)分情况讨论：
1.若是普通相交的情况，比如下图：
Pulpit rock

先判断 $\overrightarrow{p_1p_2}$ 和 $\overrightarrow{p_1p_3}$ 的叉积，以及 $\overrightarrow{p_1p_2}$ 和 $\overrightarrow{p_1p_4}$ 的叉积是否异号
Pulpit rock

再判断 $\overrightarrow{p_3p_4}$ 和 $\overrightarrow{p_3p_1}$ 的叉积，以及 $\overrightarrow{p_3p_4}$ 和 $\overrightarrow{p_3p_2}$ 的叉积是否异号
Pulpit rock

如果都异号的话（相乘小于0)，那么说明相交
2.如果有一个点与其中一个向量共线
如图， $\overrightarrow{p_3p_2}$ 和 $\overrightarrow{p_3p_4}$ 共线
Pulpit rock
那么我们只需判断p2的横纵坐标在不在p3和p4的横纵坐标之间即可
即 $min_{}$ ( $x_{p3}$ , $x_{p4}$ )<= $x_{p2}$ <= $max_{}$ ( $x_{p3}$ , $x_{p4}$ ) && $min_{}$ ( $y_{p3}$ , $y_{p4}$ )<= $y_{p2}$ <= $max_{}$ ( $y_{p3}$ , $y_{p4}$ )

物理意义

用这两个向量为两个边作一个平行四边形，平行四边形的有向面积就是叉积的结果

求凸多边形面积

求形如下图的凸n边形的面积
Pulpit rock

我们可以把这个n边形从一个点开始向其他的点连线分成n-2个三角形
Pulpit rock

因为每个三角形是叉积的绝对值的一半，所以依次求每个三角形的面积即可

long long cj(int x1,int y1,int x2,int y2){
	return x1*y2-x2*y1;
}
	for(int i=2;i<n;i++){
		int x1=p[i].x -p[1].x ;
		int y1=p[i].y -p[1].y ;
		int x2=p[i+1].x -p[1].x ;
		int y2=p[i+1].y -p[1].y ;
		int op=abs(cj(x1,y1,x2,y2))/2;
		ans+=op;
	}

求凹多边型面积

求形如下图的凹n边形的面积
Pulpit rock

如果按逆时针走的话我们可以发现：
当从p2走到p3的时候我们是往左，p3走到p4的时候往左，但是在p4走到p1的时候是往右，而 $\Delta p3p4p1$ 是凹进去的，所以我们可以先按顺序算叉积相加（不取绝对值），最后的结果取绝对值,最后的结果就是面积（如下图，绿色的面积是正的，红色的面积是负的，相加取绝对值就是最后的面积）
Pulpit rock

long long cj(int x1,int y1,int x2,int y2){
	return x1*y2-x2*y1;
}
	for(int i=2;i<n;i++){
		int x1=p[i].x -p[1].x ;
		int y1=p[i].y -p[1].y ;
		int x2=p[i+1].x -p[1].x ;
		int y2=p[i+1].y -p[1].y ;
		int op=cj(x1,y1,x2,y2)/2;
		ans+=op;
	}
    cout<<abs(ans)<<endl;

以任意点为扇心的三角形剖分

可以在多边形内找一个点，然后连向多边形的n个点，组成的所有的三角形的面积就是总面积

任意的点与多边形的n个点组成的三角形剖分

在平面内任意找一点，如果在外部，如下图：
Pulpit rock

那么我们可以发现，依次求叉积相加的结果的绝对值依旧等于三角形的面积（红色面积是负数，绿色面积是正数）
Pulpit rock

求任意多边形的面积公式

那么为了方便计算，我们可以把这个点设为原点，那么化简后的面积公式为：
A= $\frac{1}{2}$ $\sum_{i=1}^{n}$
$
\begin{bmatrix}
x_{i} &x_{i+1} \
y_{i} &y_{i+1}
\end{bmatrix}$ (i=1…n)

例题：多边形的面积

原题链接：https://www.luogu.com.cn/problem/P1183

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=110;
int n;
struct name{
	int x,y;
}p[N];
long long cj(int x1,int y1,int x2,int y2){
	return x1*y2-x2*y1;
}
signed main(){
	cin>>n;
	for(int i=0;i<n;i++){
		cin>>p[i].x>>p[i].y;
	}
	int ans=0;
	for(int i=0;i<n;i++){
		int id1=i%n;
		int id2=(i+1)%n;
		int op=cj(p[id1].x ,p[id1].y ,p[id2].x ,p[id2].y );
		ans+=op;
	}
	cout<<abs(ans)/2<<endl;
	return 0;
}

求多边形重心

给定一个简单多边形，求其重心
输入：多边形的顶点坐标（按逆时针顺序排列）
输出：重心点C的坐标
三角形的重心公式是：
x=(x1+x2+x3)/3
y=(y1+y2+y3)/3

将他分为n-2个三角形，对于每个三角形求出他的面积和重心坐标的积，所有的积相加之后除以总面积即可
设每个点与 $p_{1}$ 相连
$x_{0i}$ =( $x_{1}$ + $x_{i}$ + $x_{i+1}$ )/3
$y_{0i}$ =( $y_{1}$ + $y_{i}$ + $y_{i+1}$ )/3
$s_{i}$ =( $\overrightarrow{p_1p_i}$ × $\overrightarrow{p_1p_{i+1}}$ )/2
X=( $\sum_{i=2}^{n-1}$ $s_{i}$ × $x_{0i}$ )/ $s_{总}$
Y=( $\sum_{i=2}^{n-1}$ $s_{i}$ × $y_{0i}$ )/ $s_{总}$