目录
- 1. 优先级队列(堆)的概念
- 2. 建立大根堆(向下调整算法)
- 3. 堆插入元素(向上调整算法)
- 4. 堆删除元素(向下调整算法)
- 5. 优先级队列PriorityQueue的特性
- 6. 优先级队列PriorityQueue的构造方法(默认小根堆)
- 7. Java对象的比较
- 1. euqals方法
- 2. Comparable<>接口CompareTo方法(原类上实现)
- 3. Compartor接口Compare方法(重写一个类实现)
- 4. 三种方法的对比
- 8. 大根堆的创建
- 9. Top-k问题
- 1.整体建小根堆
- 2.局部建容量为k的大根堆
1. 优先级队列(堆)的概念
- 优先级队列PriorityQueue底层使用了堆这种数据结构,堆是一棵顺序存储的完全二叉树。
- 堆的性质
①堆中某个结点的值不大于/不小于其父节点的值(因为一旦称之为堆,则一定是大根堆or小根堆)
②堆是一棵完全二叉树(因为堆是顺序存储的二叉树,如果非完全二叉树就会存在null结点浪费了数组顺序存储的空间) - 堆是一颗完全二叉树,采用按层编号进行顺序存储,十分的高效。那么假设i为结点在数组中的下标,则有:
①i的父结点下标为(i-1)/2
②i的左孩子下标为2i+1,i的右孩子下标为2i+2
2. 建立大根堆(向下调整算法)
思路:从最后一个非叶子结点开始进行向下调整,如果父节点的值已经满足大于两个孩子结点的值,则直接跳出循环调整下一个结点;否则就与孩子结点进行交换,交换完之后可能会造成子树不满足堆的性质,因此需要继续向下调整。
建堆的时间复杂度为O(N)
向下调整的时间复杂度为O(logN)
代码:
//建立大根堆(向下调整)
public void createHeap() {
//从最后一个非叶子结点开始进行向下调整
for (int i = (usedsize-1-1) / 2; i >= 0; i--) {
shiftDown(i,usedsize);
}
}
public void shiftDown(int parent,int len) {
int child = 2 * parent + 1;
while (child < len) {
if (child + 1 < len && elem[child] < elem[child +1]) {
child = child + 1;
}
if (elem[child] > elem[parent]) {
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
parent = child;
child = 2 * parent + 1;
}else {
break;
}
}
}
3. 堆插入元素(向上调整算法)
思路:堆插入元素是直接插在有效元素的后面的【注定是最后一个叶子结点】,然后对这个叶子结点所在的位置进行向上调整,注意这个叶子不用在跟其兄弟叶子进行比较,只用跟其父结点进行比较。
向上调整的时间复杂度为O(logN)
向上调整建堆的时间复杂度为O(NlogN)
因此一般选用上下调整的算法建堆,因为最后2层的结点最多,要调整的元素也多,时间会变慢。
代码:
public void inset(int val) {
if (isFull()) {
addSize();
}
elem[usedsize++] = val;
//向上调整算法
shiftUp(usedsize-1);
}
public void shiftUp(int child) {
int parent = (child - 1) / 2;
while (parent >= 0) {
if (elem[parent] < elem[child]) {
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
child = parent;
parent = (child - 1) / 2;
}else {
break;
}
}
}
public boolean isFull() {
if (elem.length == usedsize) {
return true;
}
return false;
}
public void addSize() {
elem = Arrays.copyOf(elem,elem.length*2);
}
4. 堆删除元素(向下调整算法)
思路:每次删除的元素是堆顶的元素,将堆顶元素和堆中的最后一个元素进行交换,然后向下调整交换后的堆顶元素。
代码:
public void swap(int i, int j) {
int tmp = elem[i];
elem[i] = elem[j];
elem[j] = tmp;
}
public void deleElem() {
if (usedsize <= 0) {
return;
}
swap(0,usedsize-1);
usedsize--;
shiftDown(0,usedsize);
}
5. 优先级队列PriorityQueue的特性
- PriorityQueue中放置的元素必须要可比较,否则就不能进行向上/下调整了,并且会抛出类型转换异常ClassCastException。
- 不能插入null对象,否则会抛出空指针异常NullPointerException。
- 插入和删除元素的时间复杂度是O(logN),即树的高度。
- PriorityQueue的底层使用堆数据结构,默认是小根堆,即每次获取到的元素都是最小的。
6. 优先级队列PriorityQueue的构造方法(默认小根堆)
- 无参构造方法实例化优先级队列对象
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
底层代码:

分析:会创建一个空的优先级队列,默认容量是11
- 传入一个整型参数实例化优先级队列对象
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(100);
底层代码:
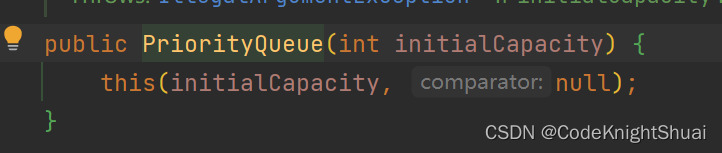
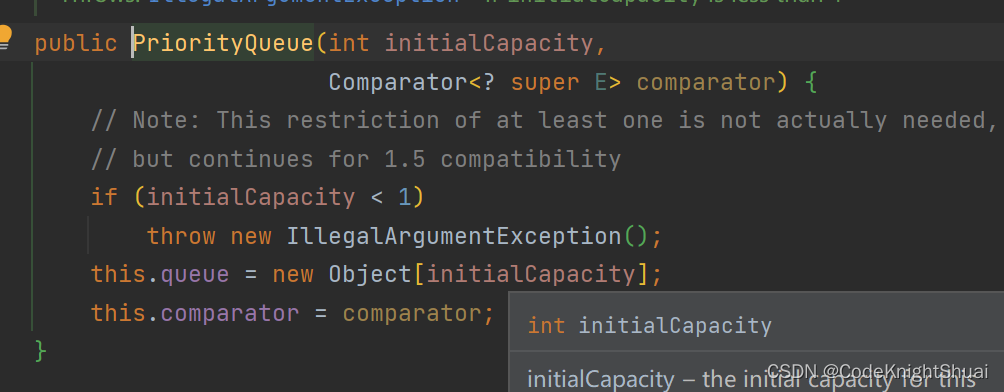
分析:会创建一个初始容量为initialCapacity的优先级队列,这里创建的容量是100,注意初始容量不能小于1,否则会抛出异常。
- 传入一个集合参数实例化优先级队列对象
LinkedList<Integer> list = new LinkedList<>();
list.add(1);
list.add(2);
list.add(3);
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(list);
分析:用LinkedList对象来构造一个优先级队列的对象。
注意:实例化优先级对象默认创建的是小根堆,如果是大根堆需要提供比较器【涉及到对象的比较】。
7. Java对象的比较
在Java中,基本数据类型可以大于、小于、等于去比较,但是对于对象的比较则需要用到以下几种方法。
1. euqals方法
①如果自定义的类没有重写euqals方法,那么默认是继承的Object类中的equals方法,使用的是“==”。

②自定义类重写equals方法
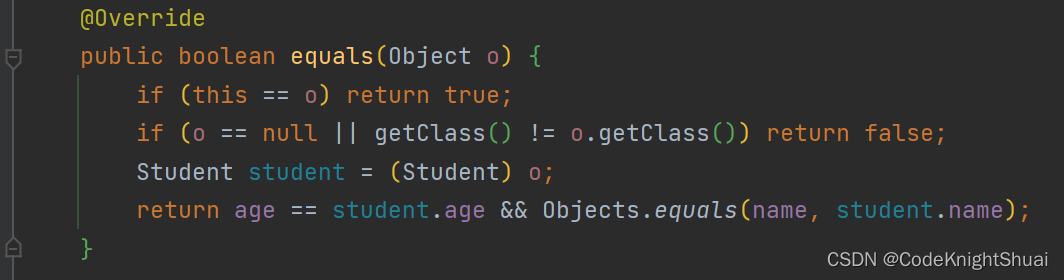
注意:euqals只能按照相等进行比较,不能比较大于、小于。
测试:
Student student1 = new Student("张三",22);
Student student2 = new Student("张三",22);
System.out.println(student1.equals(student2));
如果没有在Student类中重写euqals方法,则输出false;如果重写了euqals方法,则输出true。
2. Comparable<>接口CompareTo方法(原类上实现)
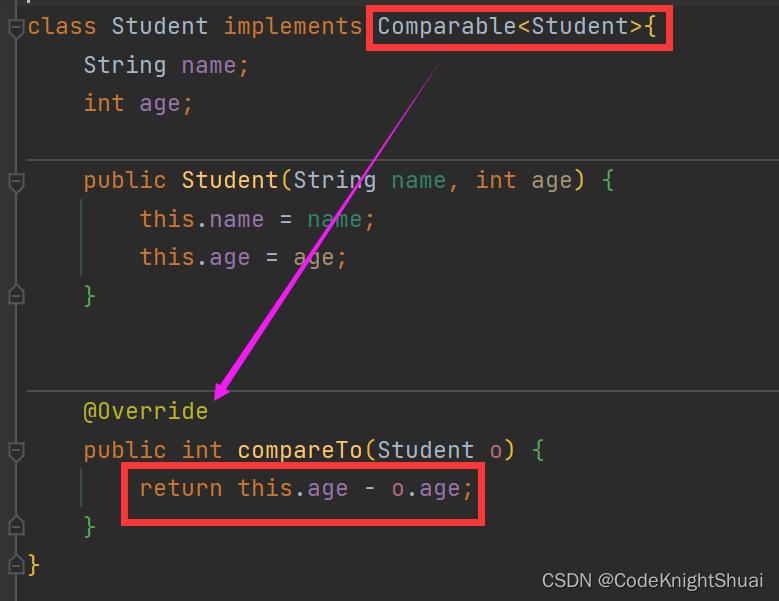
注意:
①在接口的后面要加上泛型
②这种写法侵入性比较强,不易修改
3. Compartor接口Compare方法(重写一个类实现)
class AgeComparator implements Comparator<Student> {
@Override
public int compare(Student o1, Student o2) {
return o1.age - o2.age;
}
}
实例化构造器对象,并且调用构造器中的compare方法。
public static void main(String[] args) {
Student student1 = new Student("张三",22);
Student student2 = new Student("三",22);
AgeComparator ageComparator = new AgeComparator();
System.out.println(ageComparator.compare(student1, student2));
}
4. 三种方法的对比
| 比较的方法 | 说明 |
|---|---|
| Object.equals | 不重写的话是继承Object的方法,需要重写覆写,只能比较相等与否 |
| Comparable.compareTo | 需要手动实现接口,不够灵活 |
| Comparator.compare | 需要实现一个比较器类对象 |
8. 大根堆的创建
优先级队列默认是小根堆,如果要创建大根堆,那么就传入比较方法。
比较器:(注意用到泛型)
class IntCompare implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
}
实例化比较器、优先级队列对象,并传入比较器参数
public class MaxHeap {
public static void main(String[] args) {
IntCompare intCompare = new IntCompare();
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(intCompare);
priorityQueue.offer(3);
priorityQueue.offer(2);
priorityQueue.offer(9);
priorityQueue.offer(1);
System.out.println(priorityQueue);
}
}
运行结果:
9. Top-k问题
力扣 17.14. 最小K个数
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。
示例:
输入: arr = [1,3,5,7,2,4,6,8], k = 4
输出: [1,2,3,4]
1.整体建小根堆
思路:因为有大量的数据需要排序,因此采用堆这种数据结构,把所有的数据全部建成一个小根堆,然后每次取堆顶的元素。
代码:
class Solution {
public int[] smallestK(int[] arr, int k) {
int[] ret = new int[k];
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
//小根堆
for (int i = 0; i < arr.length; i++) {
priorityQueue.offer(arr[i]);
}
for (int i = 0; i < k; i++) {
ret[i] = priorityQueue.poll();
}
return ret;
}
}
2.局部建容量为k的大根堆
思路:建立容量为k的大根堆,如果下一个待比较的元素比大根堆的元素小,就把大根堆的元素出堆,下一个待比较的元素进入堆中,这样最后得到的就是k个最小的元素。
【注意要判断数组为空 以及 k为0的情况,否则会出现空指针异常】
代码:
class IntComp implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
}
class Solution {
public int[] smallestK(int[] arr, int k) {
int[] ret = new int[k];
if(arr.length == 0 || k == 0) {
return ret;
}
//建立大根堆
IntComp intComp = new IntComp();
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(intComp);
for (int i = 0; i < k; i++) {
priorityQueue.offer(arr[i]);
}
for (int i = k; i < arr.length; i++) {
if (arr[i] < priorityQueue.peek()) {
priorityQueue.poll();
priorityQueue.offer(arr[i]);
}
}
for (int i = 0; i < k; i++) {
ret[i] = priorityQueue.poll();
}
return ret;
}
}