题目链接

Leetcode.1828 统计一个圆中点的数目

题目描述

给你一个数组 points，其中 points[i] = [xi, yi] ，表示第 i个点在二维平面上的坐标。多个点可能会有 相同 的坐标。

同时给你一个数组 queries，其中 queries[j] = [xj, yj, rj]，表示一个圆心在 (xj, yj)且半径为 rj的圆。

对于每一个查询 queries[j]，计算在第 j个圆 内 点的数目。如果一个点在圆的 边界上 ，我们同样认为它在圆 内 。

请你返回一个数组 answer ，其中 answer[j]是第 j 个查询的答案。

示例 1：

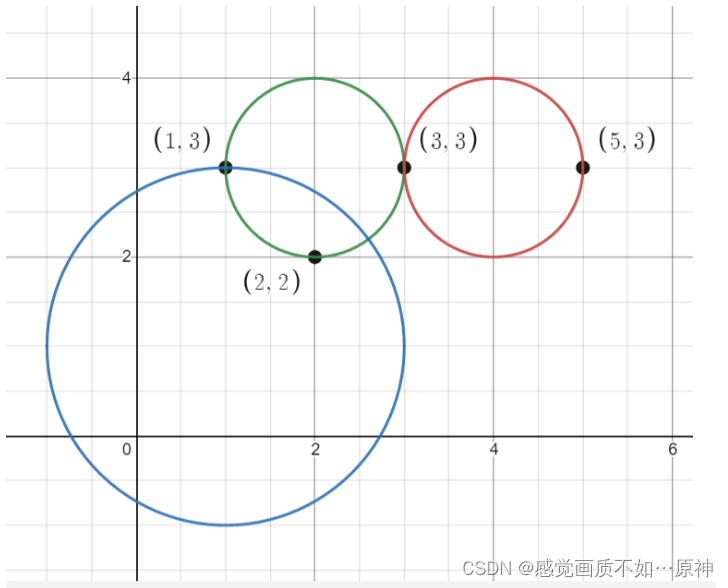
输入：points = [[1,3],[3,3],[5,3],[2,2]], queries =
[[2,3,1],[4,3,1],[1,1,2]]
输出：[3,2,2]
解释：所有的点和圆如上图所示。
queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆。

示例 2：

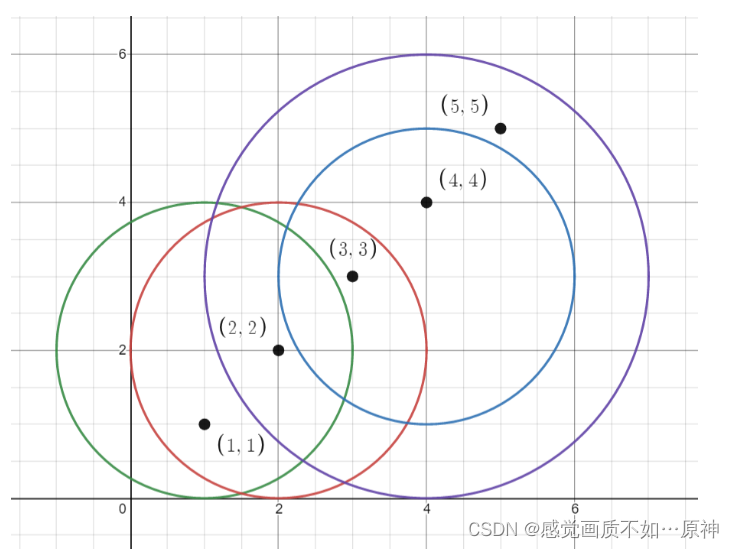
输入：points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
输出：[2,3,2,4]
解释：所有的点和圆如上图所示。
queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆，queries[3] 是紫色的圆。

提示：

• $1<=points.length<=500$
• $points[i].length==2$
• $0<=x{}_i,y_{}i<=500$
• $1<=queries.length<=500$
• $queries[j].length==3$
• $0<=x_j,y_j<=500$
• $1<=r_j<=500$
• 所有的坐标都是整数。

分析：

由于数据量只有 500，所以我们可以暴力枚举 每一个圆，points中的点是否在 圆内。

如果点 $(x,y)$ 与 圆心 $(sx,sy)$ 的距离 $<=$ 圆的半径 $r$，说明这个点 $(x,y)$ 在圆内。

时间复杂度: $O(n^2)$

C++代码：

class Solution {
public:
    vector<int> countPoints(vector<vector<int>>& points, vector<vector<int>>& queries) {
        int n = queries.size();

        vector<int> ans(n);

        for(int i = 0;i < n;i++){
            int sx = queries[i][0],sy = queries[i][1],r = queries[i][2];
            for(auto &e:points){
                int x = e[0],y = e[1];
                if((x - sx) * (x - sx) + (y - sy) * (y - sy) <= r*r) ans[i]++;
                
            }
        }
        return ans;
    }
};

Java代码：

class Solution {
    public int[] countPoints(int[][] points, int[][] queries) {
        int n  = queries.length;

        int[] ans = new int[n];

        for(int i = 0;i < n;i++){
            int sx = queries[i][0];
            int sy = queries[i][1];
            int r = queries[i][2];

            for(int[] p:points){
                int x = p[0];
                int y  = p[1];
                if((x - sx)*(x - sx) + (y - sy)*(y - sy) <= r*r) ans[i]++;
            }
        }
        return ans;
    }
}