题目链接
leetcode在线oj——组合总和(3)
题目描述
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
题目示例
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
题目提示
- 2 <= k <= 9
- 1 <= n <= 60
题目思路
我们可以使用递归,将所有可能的组合方式都排列出来,然后验证其总和是否为n,如果是n就将结果添加到list中
我们需要一个全局变量list,在所有递归中使用,并且递归需要定义当前的位置,1-9一共n个,数字总数k,需要的组合的总和sum,如果当前list的size已经超过k,或者就算当前list加上后面所有的数字都无法到达k个,说明已经不满足条件了,就返回上一个状态
如果当前list的size正好等于k,那么就验证list所有数字加起来是否为n,是就添加进result中,否则就返回上一个状态
完整代码
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> list = new ArrayList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
dfs(1, 9, k, n);
return result;
}
private void dfs(int cur, int n, int k, int sum) {
if(list.size() + (n - cur + 1) < k || list.size() > k){
return;
}
if(list.size() == k){
int count = 0;
for (int x:list) {
count += x;
}
if(count == sum){
result.add(new ArrayList(list));
return;
}
}
list.add(cur);
dfs(cur + 1, n, k, sum);
list.remove(list.size() - 1);
dfs(cur + 1, n, k, sum);
}
}
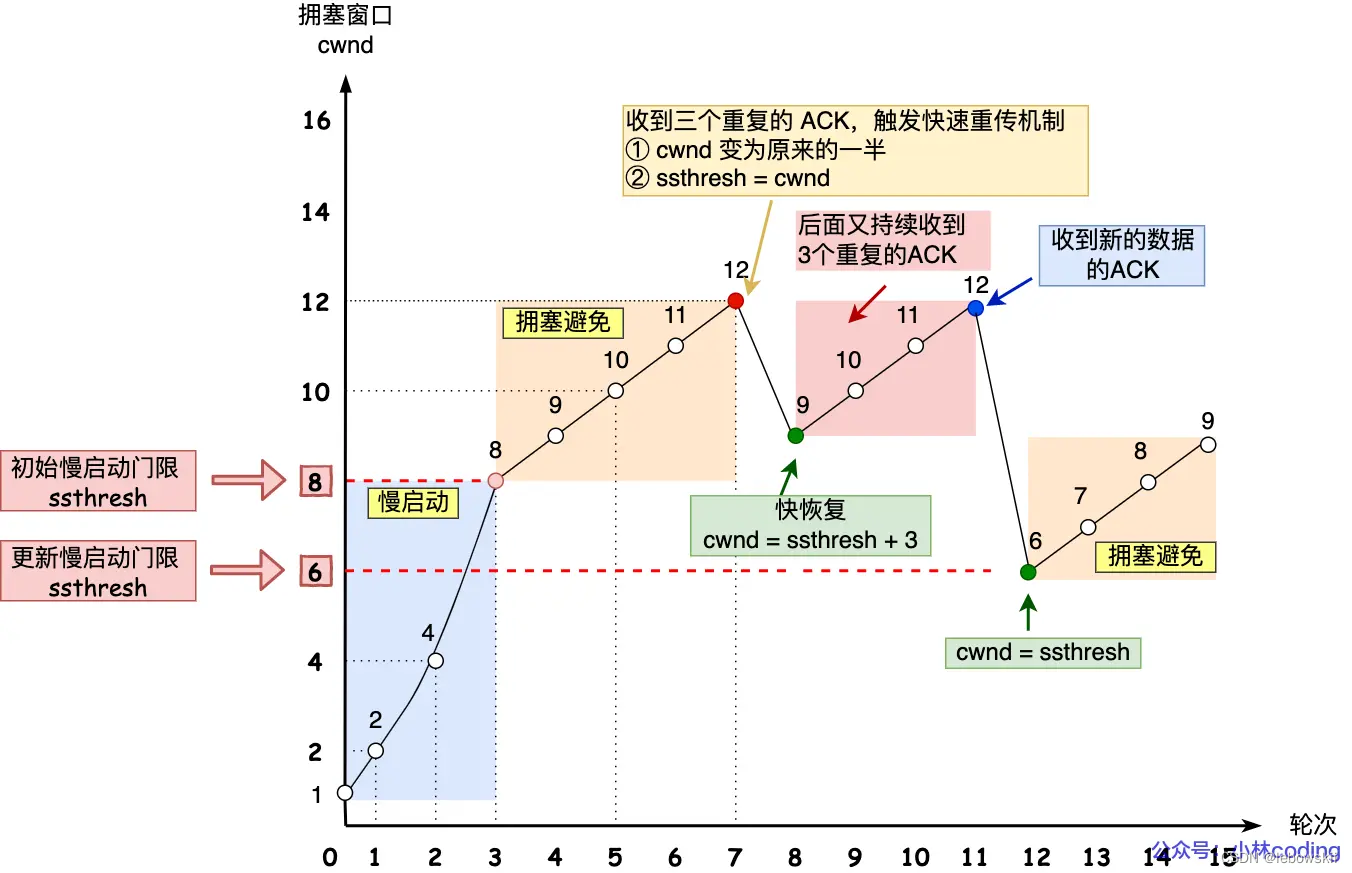
代码执行流程图












![[QMT]08-从本地行情数据解析历史K线信息](https://img-blog.csdnimg.cn/img_convert/d0b88aeecb825ce13e0c96487e05008b.png)