3.1 6个三角函数的演化进程简述

3.2 Johann M¨uller(别名Regiomontanus)的贡献

第3章 6个三角函数的成熟过程

It is quite difficult to describe with certainty the beginning of trigonometry . . . . In general, one may say that the emphasis was placed first on astronomy, then shifted to spherical trigonometry, and finally moved on to plane trigonometry(很难确切地描述三角学的起源……一般而言，人们可以说，应当强调它首先基于天文学，然后再转向球面三角，最后转向平面三角)。

——Barnabas Hughes, Regiomontanus关于三角形的介绍

3.1 6个三角函数的演化进程简述

一部早期的印度教(Hindu)天文学著作<<Surya Siddhanta>>(约公元400年)，基于Ptolemy’s的和弦表制定了半弦表(见图15)。但是，明确提到将正弦(sine)作为一个函数对待的著作是Aryabhata(约公园前510年)的<<Aryabhatiya>>，被认为是最早的印度教纯数学论文。[1] 在这部著作(也被称为长老Aryabhata；生于公元约475年或476年，死于约公元550年)[2]中给称半弦(half chord)为“ardha-jya”,他有时又反过来称半弦为弦半(chord half)，写为“jya- ardha”；将某个适当的时候，他将其简写为“jya”或“jiva”。

现在以一个有趣的词源演化开始，引出我们现代的词“sine。” 当阿拉伯将“Aryabhatiya”翻译成他们自己的语言的时候，他们保留了词汇“jiva”，并没有将其翻译，在阿拉伯语中——也和在希伯来语中一样，词汇中包含大部分的辅音，通过常用用法理解缺失元音的发音。“jiva”可以读成“jiba”也可以读成“jaib”, jaib”在阿拉伯语中指的是胸脯(bosom)，折叠(fold)，海湾(bay)。当阿拉伯语的版本翻译成拉丁语版本的时候，“jaib”就被翻译成了“sinus”，其意义为胸脯(bosom)，海湾(bay)或者曲线(curve)(在月球(lunar)地图上，类似海湾(bays)的区域仍被描述为窦状(sinus)(下陷或凹下去的地方))。我们在Cremona(大约公元1114–1187年)的Gherardo的著作中发现这个词“sinus”，Gherardo翻译将很多古希腊著作包括“Almagest”从阿拉伯语翻译成拉丁语(译注：大概当时有很多古希腊著作被翻译成了阿拉伯语，由于原版古希腊版本遗失或者战乱丢失，要获得古希腊著作，只能间接从其阿拉伯语版本中转译成拉丁语了)。其它作者就跟从这种做法，很快，这个词“sinus”——或者在其英文版本中对应词“sine”——在整个欧洲数学教科书中变得很常见了。第一次使用缩记法“sin”的人是Edmund Gunter(伦敦数学家甘特)，但是一位英国牧师，后来成为伦敦格雷欣学院(Gresham College)的天文学教授。在1624年，他发生了一个称为“冈特标尺(Gunter scale)”的机械装置，用于对数(logarithms)计算——这是我们所熟悉的滑尺的先驱——符号“sin”(以及“tan”)首次出现在描述他的发明的图纸中。[3]

--------------------图15 <<Surya Siddhanta>>中的一页--------------------------

数学符号经常出现意想不到的变化。正如Leibniz在使用符号表示乘法的问题上反对William Ougthred使用的符号“×”(原因是它类似于字母“x”)，Carl Friedrich Gauss (1777–1855)反对使用 $sin^{2}\Phi$ 作为sinΦ的平方，也是如此：

“我认为 $sin^{2}\Phi^{}$ 是可憎的，尽管Laplace使用了它；如果担心不写成 $sin^{2}\Phi$ 可能容易引起混淆，而不写成这样引起混淆的情况可能永远也不会发生……，如果真的怕引起混淆，让我们把它写作 $(sin\Phi )^{2}$ 而不是 $sin^{2}\Phi$ ，因为以此类推，应该表示为sin(sinΦ)。”[4]

尽管(Notwithstanding) Gauss反对这种记法，符号 $sin^{2}\Phi$ 还是存活了下来，但是他担忧容易与sin(sinΦ)混淆也不是没有道理的：今天，函数对不同初始值的重复应用是活跃研究的主题，而且，像(sin(sin...(sinΦ)...))这样的表达式在数学文化上的出现已是常态。

其余五个三角函数的历史更近。我们今天认为与正弦同等重要的余弦函数，最初是由于需要计算余角的正弦而产生的。Aryabhata将它称为“kotijya”，使用它的方式与现代复古三角表的使用方式大致相同(直到手持式计算器使它们过时)，都是通过在同一列中列出从 0°到 45°的角度的正弦和互补角度的余弦。“cosinus”这个名字出自Edmund Gunter:他写作“co.sinus”，John Newton (1622–1678) 在1658年将其改为“cosinus”，他是一个老师，也是数学教科书的作者(他与Isaac Newton没有关系，不是同一人)。第一次使用缩记法“cos”的人是Jonas Moore (1617–1679),他在1674年首次开始使用缩记法，他是一位英国数学家和测量师(surveyor)。

函数正割(secant)和余割(cosecant)出现得甚至更晚。在阿拉伯学者Abul-Wefa(940–998)的著作中首次涉及它们的时候，并没有专门的名称，Abul-Wefa也是首批构造正切表(tangent table)的作者之一；但在15世纪航海表(navigational tables)被计算出来之前，它们几乎没有用处。第一个印刷的正割表出现在Georg Joachim Rhæticus(1514-1576年)的著作<<三角教义准则>>(Canon doctrinae triangulorum)(1551 年在Leipzig(莱比锡)出版)中，他师从哥白尼(Copernicus)并成为哥白尼的第一个弟子(disciple)； 在这部著作中，所有六个三角函数都是第一次出现。1626 年，生于法国的数学家阿尔伯特·吉拉德(Albert Girard，1595-1632年)建议使用符号“sec“，他一生的大部分时间都在荷兰(Holland)度过。(Girard是第一个理解几何问题中负根的含义的人；他还猜测多项式的根与其次数一样多，并且是代数中使用括号的早期倡导者。) 对于sec A 他写作

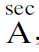
对于tan A有类似的符号，但对于sin A和cos A，他分别写为 A 和 a。正如我们所见，正切比和余切比起源于日晷(guǐ)和影子计算法。但是将这些比率作为角度的函数来处理是从阿拉伯人开始的。第一张正切和余切表由 Ahmed ibn Abdallah al-Mervazi(通常称为Habash al-Hasib(“计算机(computer)”))于860年左右构建，他撰写了有关天文学和天文仪器的著作。[5] 天文学家al-Battani(在欧洲被称为 Albategnius；出生于加利福尼亚州美索不达米亚的巴坦(Battan)，大于生于858年，卒于929年) 给出了根据高度为h的垂直表投射的阴影的长度s来计算太阳在地平线上的高度的规则；他的规则是(大约920年):

$s=\frac{hsin(90^{\circ}-\Phi )}{sin\Phi },$

相当于公式 s = h cotΦ 。请注意，在表达它时，他只使用了正弦函数，其他函数的名称尚不为人所知。(正是通过al-Battani的工作，印度教的半弦函数——我们现代的正弦函数——才得以在欧洲广为人知。) 根据这个规则，他构建了一个“阴影表”——本质上是一个余切表——从1° 到90 °的每一度的余切值。

直到1583年，丹麦数学家Thomas Fincke (1561-1646 年)在他的著作<< Geometria Rotundi>>(圆的几何)中使用了现代名称“tangent”，这个现代名称才首次出现；直到那时，大多数欧洲作家仍然使用来自阴影计算的术语：“umbra recta”(直影)表示垂直指针投射的水平阴影，“umbra versa”(转动的阴影)表示通过附着在墙上的日晷(guǐ)指针投射的垂直阴影。Edmund Gunter于1620 年首次使用“cotangens”[sic] 一词。人们建议使用各种缩写来表示这些函数，其中包括William Oughtred (1657年)提出的t和 t co 和William Oughtred(1657年)提出的 T 和 t以及John Wallis(1693)。但第一个坚持使用此类缩写的是英国数学家和测量员理查德·诺伍德(Richard Norwood，1590-1665年)；在1631年于伦敦出版的三角学著作中，他写道：“In these examples s stands for sine:t for tangent: sc for sine complement [i.e., cosine]: tc for tangent complement: sec for secant(在这些例子中，s表示sine: t表示tangent: sc表示sine complement(即，cosine)：tc表示tangent complement: sc表示secant)。”我们注意到，即便是在今天,这些函数也没有统一的符号，欧洲课本经常使用“tg”和“ctg”来表示正切和余切。

“tangent”一词来自拉丁语“tangere”，词义为“to touch”(触摸)；它与正切函数的关联可能来自以下观察：在圆心为 O 且半径为 r 的圆中(图16)，令AB为圆心角2α对向的弦，OQ 为圆心角的二等分线(bisector)。画一条平行于 AB 并在 Q 处与圆相切的线，并延长 OA 和 OB 直到它们分别在 C 和 D 处与这条线相交。我们有等式

AB = 2r sin α ，CD = 2r tan α ，

表明正切函数与切线的关系就像正弦函数与弦的关系一样。实际上，这种构造构成了单位圆上六个三角函数的现代定义的基础。

-------------------图16 AB = 2r sin α ，CD = 2r tan α---------------------------

通过经典希腊语和印度教教材的阿拉伯语翻译，代数和三角学的知识逐渐传播到欧洲。在8世纪，欧洲通过穆罕默德·伊本·穆萨·花拉子米( Mohammed ibn Musa al-Khowarizmi,约780年——约 840 年)的著作介绍了印度数字——我们现代的十进制记数系统。他的伟大著作的标题“ilm al-jabr wa'l muqabalah”(减少和抵消的科学)被音译为现代词“algebra (代数)”，他自己的名字演变为“algorithm(算法)”一词。印度-阿拉伯系统并没有立即被公众接受，他们更喜欢使用旧的罗马数字。然而，学者们看到了新系统的优势并热情地提倡它，使用古老的算盘(abacus)进行计算的“算盘师(abacists)”和使用纸笔象征性地进行计算的“算术师(algorists)”之间的竞赛成为中世纪欧洲的一个共同特征。

主要是通过列奥纳多·斐波那契(Leonardo Fibonacci)在他的<<算盘书>>(Liber Abaci) (1202)中对印度-阿拉伯数字的阐述，十进制系统才最终在欧洲得到了普遍应用。Georg von Peurbach(1423-1461)在1460年左右计算出第一个使用新系统的三角函数表。但他的学生 Johann Müller(1436–1476年)，人称Regiomontanus(因为他出生在柯尼斯堡(K¨onigsberg)，在德语中意为“the royal mountain (皇家山脉)”)，撰写了迄今为止第一部关于三角学的综合论文。在他的论文“De triangulis omnimodis libri quinque”(“关于每种三角形的五部书，”大约在1464年) [6] 他从基本的几何概念开始发展了这个主题，并引导到了正弦函数的定义；然后，他展示了如何使用角度的正弦或其补角的正弦(余弦)求解任何三角形(平面或球面)。正弦定律在这里以口语化的形式表述，求三角形面积的规则也是如此,A = (ab sin γ)/2。奇怪的是，不存在正切函数，可能是因为这项工作的主要推力是球面三角学，其中正弦函数占主导地位。

“De triangulis”是当时最具影响力的三角学著作；它的副本到了哥白尼手中，他对其进行了彻底的研究(见第45页)。然而，又过了一个世纪，“三角学(trigonometry)”这个词才出现在书名中。这一荣誉授予 Bartholom¨aus Pitiscus(1561-1613年)，他是一位主要兴趣是数学的德国牧师。他的书<<Trigonometriae sive de dimineme triangulorum libri quinque>>(关于三角学，或关于三角形的性质的五部书)于1595年在法兰克福出版。这将我们带到了17世纪初，当时三角学开始采用从那以后它将保留的分析特征。

注释和来源：

1. Aryabhata 的 Aryabhatiya：一部关于数学和天文学的古代印度著作(The Aryabhatiya of Aryabhata: An Ancient Indian Work on Mathematics and Astronomy)，由Walter Eugene Clark翻译并附注(芝加哥：芝加哥大学出版社，1930年)。在这项工作中（第 28 页），的值为3.1416；这是以口语化形式表述一系列数学指令，这是印度数学的一个共同特征。另见David Eugene Smith, <<History of Mathematics>>,(1925;New York重印: Dover, 1958), 卷一卷153–156页, 以及George Gheverghese Joseph, <<The Crest of the Peacock: Non-European Roots of Mathematics>>(孔雀之冠：数学的非欧洲根源) (Harmondsworth，英国：Penguin Books，1992 年)，第 265–266 页。

2. 1975 年，印度以他的名字命名了第一颗卫星。

3. 有关三角符号的详细历史，请参阅 Florian Cajori，<<A History of Mathematical Notations>>(数学符号史)(1929 年；芝加哥重印：Open Court，1952 年)，第 2 卷，第 142–179 页；另Smith，<<History of Mathematics>>(数学史)，第 2 卷，第 618–619 和 621–623 页。可以在Vera Sanford,<<A Short History of Mathematics>>(数学简史) (1930; Cambridge重印, Mass.: Houghton Mifflin, 1958),第298页中找到三角函数符号及其作者和日期的列表。

4. 高斯-舒马赫通信，罗伯特·爱德华·莫里茨(Robert Edouard Moritz) <<On Mathematics and Mathematicians >>(论数学与数学家)(Memorialia Mathematica) (1914年；摘自New York重印：Dover，1942年)，第318页。

5. Smith，<<History of Mathematics>>(数学史)，第 2 卷，第 620 页。然而，Cajori 认为 al-Battani 是第一个构建余切表的人(<<A History of Mathematics>>，1893 年；第 2 版。New York：Macmillan，1919 年，第 105 页)。

6. Barnabas Hughes(麦迪逊：威斯康星大学出版社，1967年)的英文译本，附有简介和注释。

3.2 Johann M¨uller(别名Regiomontanus)的贡献

直到16世纪，三角学主要由天文学家发展，这并非巧合。Aristarchus和Hipparchus 是天文学家，他们创立了三角学作为数学的一个独特分支，还有《天文学大成》的作者托勒密。在中世纪，阿拉伯和印度教的天文学家，特别是撒马尔罕(Samarkand，1393–1449)的Abul-Wefa、al-Battani、Aryabhata 和 Ulugh Beg(1393-1449年)吸收了希腊的数学遗产并极大地扩展了它，尤其是在球面三角学(spherical trigonometry)方面。当这一综合遗产传到欧洲时，走在前列的又是一位天文学家：Johann Müller(见图 17)。

Müller于1436年出生在下弗兰肯(Lower Franconia)行政区柯尼斯堡镇(K¨onigsberg)附近的Unfinden(这不是东普鲁士(East Prussia)更有名的K¨onigsberg——现在的加里宁格勒(Kaliningrad))。他名字的不同版本得以流传：Johannes Germanus(因为他是德国人)、Johannes Francus(因为Franconia也被称为法国东部)和以Königsberg镇命名的Johann von Kunsperk。按照他那个时代学者的做法，他采用了一个拉丁名字Regio Monte，这是德语单词“K¨onigsberg”(“皇家山脉”) 的直译，并在适当的时候被称为Regiomontanus。然而，即使是这个名字也有多个版本：法国科学家皮埃尔·加森迪(Peter Gassendus，1592-1655年)撰写了雷吉奥蒙塔努斯(Regiomontanus)的第一部权威传记，称他为“Joannes de Monte Regio”，具有独特的法语发音。[1]

-----------------------图17 Regiomontanus素描-------------------------------

Regiomontanus 早年在家学习。十二岁时，他的父母将他送到莱比锡接受正规教育，毕业后他搬到维也纳，十五岁时从维也纳大学获得学士学位。在那里，他遇到了数学家和天文学家乔治·冯·佩尔巴赫(Georg von Peurbach，1423-1461年)，并与他们建立了亲密的友谊。佩尔巴赫师从库萨(Cusa)红衣主教尼古拉斯(Cardinal Nicholas)(1401-1464 年)，但拒绝了后者关于地球可能围绕太阳运动的推测。他是托勒密(Ptolemy)的仰慕者，并计划根据现有的拉丁文译本出版校正版的<<天文学大成>>。他还着手准备一个新的、更准确的正弦表，使用最近采用的印度-阿拉伯数字。年轻的Regiomontanus 很快受到了Peurbach 的影响，他们之间的关系达到了父子关系的强度。但随后Peurbach突然去世，年仅38岁。他的英年早逝使他的计划未能实现，他的学生也感到震惊。

Peurbach临终前委托他年轻的学生完成天文学大成的翻译。Gassendi在他的 Regiomontanus传记中写道：“This became a sacred trust for the fatherless student(这成为孤儿学生的神圣托付)。”[2] Regiomontanus完全献身于这项任务，学习希腊语以便他能够阅读托勒密的原著。在他的工作过程中，他对古老的希腊文和拉丁文手稿产生了兴趣，无论走到哪里，他都会获得这些手稿；他的奖品之一是他在1464年发现的丢番图 (Diophantus)的不完整手稿。他赢得了许多学者的友谊，其中包括克里特岛的乔治·特拉比松(Georgius Trapezuntios, 1396-1486)，他是托勒密的权威，翻译了天文学巨著和席恩的著作，并把他们的评注翻译成了拉丁文。然而，当Regiomontanus批评Trebizond 在解释评注时犯下严重错误，并称他为“the most impudently perverse blabber-mouth(最无礼、任性、喋喋不休的人)”时，这种友谊就变坏了。 [3]这些话，据某种说法，会带来糟糕的后果。

他多次旅行去希腊和意大利，在那里他参观了帕多瓦(Padua)、威尼斯(Venice)和罗马(Rome)。1464年，他在威尼斯完成了他最为人熟知的著作<<论各种三角形>>(见下文)。除了所有这些活动之外，Regiomontanus还是一名实践占星家(practicing astrologer)，他认为这项活动与他的科学工作之间没有矛盾(两个世纪后伟大的天文学家约翰内斯开普勒(Johannes Kepler)也会这样做)。1467年左右，他应匈牙利(Hungary)国王Mathias Huniades Corvinus的邀请，担任布达佩斯(Budapest)新成立的皇家图书馆的图书管理员；国王刚刚从与土耳其人的战争中胜利归来，并带回了许多珍贵书籍作为战利品，他发现Regiomontanus是管理这些宝藏的理想人选。在Regiomontanus到来之后不久国王就病倒了，他的顾问们预测他即将死去。然而，Regiomontanus利用他的占星术技能将这种疾病“诊断(diagnose)”为仅仅是最近一次日食引起的心脏衰弱！瞧，国王康复了，并赐予Regiomontanus许多奖赏。

Regiomontanus于1471年返回故乡，定居在靠近他出生地的纽伦堡(N¨urnberg)。这座以悠久的学习和贸易传统而闻名的城市刚刚开设了一家印刷厂，Regiomontanus看到了它提供的传播科学文字的机会(就在几年前，即1454年，约翰·古腾堡(Johann Gutenberg)发明了活字印刷术)。他创立了自己的出版社，并准备着手一项雄心勃勃的科学手稿印刷计划，但这些计划因他的早逝而中断。他还建立了一个天文台，并配备了著名的纽伦堡工匠所能生产的最好的仪器；其中包括浑天仪(armillary spheres)和测量天体之间角距(angular distances)的装置。

Regiomontanus是第一个商业用途的数学和天文学书籍的出版商。1474年，他印制了他的星历表，这些表列出了1475年至1506年间每一天的太阳、月亮和行星的位置。这项工作为他带来了极大的赞誉；克里斯托弗·哥伦布(Christopher Columbus)在他第四次航行到新大陆时得到了它的副本，并用它来预测1504年2月29日著名的月食。敌对的当地人有一段时间拒绝给哥伦布的人提供食物和水，他警告他们，上帝会惩罚他们，夺走月光。他的警告起初遭到嘲笑，但当日食在指定的时间开始时，惊恐的当地人立即悔改并屈服。

1475年，教皇西克斯图斯四世(Pope Sixtus IV)号召Regiomontanus来到罗马，帮助他修改旧的儒略历(Julian calendar)，该历法与季节严重不协调。不情愿地，他辞去了许多职责，前往永恒之城。1476年7月6日，他在四十岁生日的一个月后突然去世。他的死因尚不清楚：一些人将其归咎于瘟疫，另一些人将其归咎于一颗路过的彗星。然而，一直有传言说Regiomontanus是被Trebizond的儿子毒死的，他们从未忘记他对父亲翻译Theon对托勒密的评论的尖锐批评。[4] 当他去世的消息为人所知时，纽伦堡开始公开哀悼。[5]

Regiomontanus最有影响力的作品是他的<<De triangulis omnimodis>>(论各种三角形)，这是一部以欧几里得几何原理为蓝本的分为五部分的著作(“书籍”)(图18)。在这部著作中，他将托勒密以及印度教和阿拉伯学者的三角学遗产组织成一个系统的知识体系。第一册从基本概念的定义开始：数量、比率、相等、圆、弧和弦。正弦函数是根据印度教定义引入的：“当弧及其弦被平分时，我们称该半弦为半弧的右正弦。” 接下来是公理列表，接着是处理平面三角形几何解的56个定理。大部分材料涉及几何而不是三角学，但定理20 介绍了在求解直角三角形时使用正弦函数。

----------图18<<论各种三角形>>的标题页(N¨urnberg, 1533)--------------------

真正的三角学在第二卷中开始阐述正弦定理；与所有其他规则一样，这是按字面说明而不是用符号表示的，但其表述与当今任何教科书中一样清晰。然后使用正弦定律解决斜三角形的SAA和SSA情况。这里也第一次出现(虽然是隐含地出现)，三角形面积的公式是依据两条边和夹角：“如果三角形的面积与两条边构成的矩形的面积同时已知，那么与底边相对的角度要么已知，要么[那个角度]连同[它的]已知[外部]等于两个直角。”[6] 按现代的公式，也就是说，从这个公式A = (bc sin α)/2 ，如果已知面积A两条边b和c的乘积，你可以求出角α或者(180°- α)。奇怪的是，Regiomontanus 从未使用过正切函数，尽管他一定从1467年的正切表Peurbach中熟悉了它，当然还从阿拉伯人将它用于影子计算的应用熟悉了它。[7]

其余三部书涉及球面几何和三角学，它们都是天文学中必不可少的工具。正如他在引言中所述，Regiomontanus在<<论三角形>>中的主要目标是对天文学进行数学介绍。他用可能摘自现代教科书的话告诫读者要仔细研究这本书，因为它的主题是理解天空(heavens)的必要先决条件：

You, who wish to study great and wonderous things, who wonder about the movement of the stars, must read these theorems about triangles. . . . For no one can bypass the science of triangles and reach a satisfying knowledge of the stars. . . . A new student should neither be frightened nor despair. . . . And where a theorem may present some problem, he may always look down to the numerical examples for help(想要研究伟大而奇妙的事物，想知道星星的运动的人，必须阅读这些关于三角形的定理。……因为没有人可以绕过三角形的科学并获得令人满意的星星知识。……新手既不应该害怕也不应该绝望。……在定理可能出现问题的地方，他可能总是看数值例子寻求帮助)。 [8]

Regiomontanus于1464 年完成了<<论三角形>> (On Triangles) 的写作，但直到 1533 年才出版，即他死后半个多世纪。通过16世纪上半叶德国领先的数学天文学家乔治·约阿希姆·雷提库斯(George Joachim Rhæticus，1514-1576 年)，它传到了尼古拉斯·哥白尼(Nicolas Copernicus，1473-1543年)那里。 Rhæticus 于1539 年拜访哥白尼并成为他的第一个学生；尽管Rhæticus比哥白尼小四十一岁，但两人一起学习，前者在数学方面指导后者。(正是在Rhæticus 的坚持不懈的推动下，哥白尼最终同意出版他的伟大著作<<论革命>>(De revolutionibus)，在其中阐述了他的日心系统。) 这份副本幸存了下来，并显示了哥白尼笔迹的许多旁注。[9] 后来，伟大的丹麦观测天文学家第谷·布拉赫(Tycho Brahe, 1546–1601)以该作品为基础计算了仙后座著名的新星(新星)的位置， 1572年，他有幸目睹了他的出现。因此，Regiomontanus 的工作奠定了很多数学基础，帮助天文学家塑造了我们对宇宙的新看法。

在1471 年，Regiomontanus 在给爱尔福特(Erfurt)大学教授Christian Roder的一封信中提出了以下问题：“垂直悬挂的杆在地面上的哪个点看起来最大 [即，对着最大的视角]？”据称这是自古以来数学史上的第一个极值问题。[10]

在图19中，我们令垂直线段AB表示杆。令OA = a, OB = b,且OB = x，其中P是地平面上的一点，以这一点为顶点的角θ = ∠BPA是影子与杆投影形成的最大角。令α = ∠OPA, β = ∠OPB 。我们有

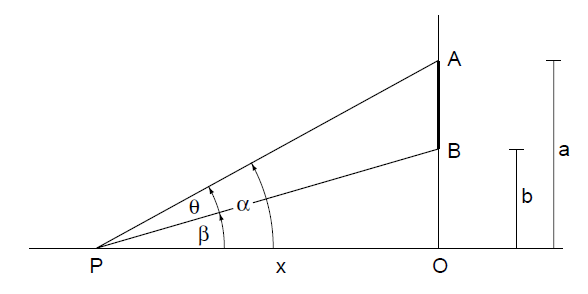
$cot\theta =cot(\alpha -\beta )=\frac{cot\alpha cot\beta +1}{cot\beta -cot\alpha }=\frac{(\frac{x}{a})(\frac{x}{b})+1}{\frac{x}{b}-\frac{x}{a}}=\frac{x}{a-b}+\frac{ab}{(a-b)x}$

图19 Regiomontanus的最大值问题: x在什么距离线侧面AB正对的角θ最大。

我们现在可能倾向于微分这个表达式，以便找到使它最小化的 x 值(因为cot θ随着随着角度θ从0° 递增到90°，其值是递减的，θ的最大值意污染着cot θ的最小值)。但是 Regiomontanus生活在微积分发明的200年前，所以让我们将自己的思维限定在初级方法上。我们将使用代数中的一个定理：两个正数u和v的算术平均值永远不会小于它们的几何平均值，并且当且仅当这两个数相等时，这两个平均值才相等。用符号表示，即

$(u+v)/2\geq \sqrt{uv}$

等号成立的条件是当且仅当 u=v 。[11]

将

$u=\frac{x}{a-b},v=\frac{ab}{(a-b)x}$

代入公式，我们得到

$cot\theta =(u+v)\geq 2\sqrt{uv}=\sqrt{\frac{x}{a-b}.\frac{ab}{(a-b)x}}=\frac{2\sqrt{ab}}{a-b}$

要使等号成立，当且仅当

$\frac{x}{a-b}=\frac{ab}{(a-b)x}$

成立，即当

$x=\sqrt{ab}$

时成立。

因此，所需点的距离等于杆的上端点和下端点的高度的几何平均值，从杆的底部水平测量。

这个结果提供了一个有趣的几何解释：使用直尺(straightedge)和圆规(compass)，构造通过A和B并与地面相切的圆(图 20)。根据一个众所周知的定理，我们有

$OA.OB = (OP)^{2}$ ，

即，

$ab=(x)^{2}$ ,

因此，有

$x=\sqrt{ab}$ 。

相反，我们可以很容易地说服自己，通过 A、B和所需点P的圆一定与地面相切；因为如果它在R和S两点截断地面(图 21)，那么R和S之间任何点P的对角将大于R或S处的角度(P现在是地面的内点)圆)，而P 处的角度应该是最大的。因此Regiomontanus的问题可以通过简单的几何构造来解决。[12]

---------------------------------图20 几何解的证明---------------------------

我们只能推测是什么促使 Regiomontanus提出这个问题。它可能起源于建筑学或透视学中的一个问题：找到观看高层建筑窗户的最佳位置。透视法——根据物体在眼睛中的真实外观来绘制物体的技术——在当时是一个新颖的主题，由意大利文艺复兴时期的艺术家菲利波·布鲁内莱斯基(Filippo Brunelleschi，1377-1446年)和莱昂内·巴蒂斯塔·阿尔贝蒂(Leone Battista Alberti，1404-1472 年)引入。 (著名艺术家阿尔布雷希特·丢勒 (Albrecht Durer)是一位主要的透视学作家，他出生于纽伦堡，同年雷吉奥蒙塔努斯 (Regiomontanus) 定居于此。) 它很快成为艺术的核心学说，并且它把两个看似陌生的学科——艺术和几何学——并列在一起——与文艺复兴时期的普遍主义理想相吻合。Regiomontanus很可能是为了回应一位艺术家或建筑师的询问而提出他的问题。

注释和来源：

1. 参见<<Regiomontanus on Triangles>>(Regiomontanus论三解开) ，由Barnabas Hughes翻译并导读和评注(麦迪逊：威斯康星大学出版社，1967年)，第11-17页，这幅传记素描就是从中改编的。另见David Eugene Smith，<<History of Mathematics>>(数学史)(1923年初版；New York再版：Dover，1958)，卷1，第259-260页。Regiomontanus 唯一的现代传记是德文的：Ernst Zinner, << Leben und Wirken des Johannes M¨uller von K¨onigsberg genannt Regiomontanus>> (Munich:C. H. Beck, 1939)。

2. 与Hughes 所引用的一样，<< Regiomontanus on Triangles>>，第13页。

3. 同2.，第14页。

4. 加森迪(Gassendi)于1654年出版的雷吉奥蒙塔努斯(Regiomontanus)传记讲述了他中毒身亡的故事，这让人联想到安东尼奥·萨列里(Antonio Salieri)据称毒死了他的主要竞争对手莫扎特(Mozart)。

5. 法国人文主义者彼得·拉穆斯(Pierre de la Ram´ee，1515-1572年)认为 Regiomontanus 发明了一种机械苍蝇，它可以离开人的手，在房间里嗡嗡作响，然后回到人的手上，而一只老鹰可以离开城市，飞去迎接即将到来的权贵，然后陪他回城。(Hughes，Regiomontanus on Triangles，第17页)。这些故事无疑是夸张的，但它们反映了雷吉奥蒙塔努斯受到他的同胞们的高度尊重。用拉穆斯的话来说，“塔伦托(Tarento)有它的阿基塔斯(Archytas)，锡拉丘兹(Syracuse)有它的阿基米德(Archimedes)，拜占庭(Byzantium)有普罗克洛斯(Proclus)，亚历山大·克特西比乌斯(Alexandria Ctesibius)和纽伦堡雷吉奥蒙塔努斯(N¨urnberg Regiomontanus)。……塔伦托和锡拉丘兹、拜占庭和亚历山大的数学家都走了。但在纽伦堡的大师中，学者们的喜悦是数学家Regiomontanus。”

6. 同5.的引用<< Regiomontanus on Triangles>>，下同，第133页。

7. 同5.的引用，第4-7页。

8. 同5.的引用，第27-29页。

9. 同5.的引用，第9页。

10. Heinrich D¨orrie, <<100 Great Problems of Elementary Mathematics:Their History and Solution>>(100个初等数学的伟大问题：它们的历史和解)，由David Antin翻译,(1958初版; NewYork再版: Dover, 1965)，第369-370页。我稍微更改了用词，以便更容易阅读。

11. 该定理源于实数的平方永远不会为负的事实。因此,

$0\leq \left (\sqrt{u}-\sqrt{v} \right )^{2}=u-2\sqrt{uv}+v$ 。

将 $-2\sqrt{uv}$ 移到左边再除以2，我们就得到了所要求的结果。等号成立仅当 $\sqrt{u}-\sqrt{v}=0$ 时，即u = v时。

12. 我无法确定Regiomontanus是否真的提供了解决方案。根据Florian Cajori(<<A History of Mathematical Notation>>(数学符号史，1928初版, La Salle, Ill.: Open Court, 1951, 卷1, 第95页 )，Regiomontanus在1463年至1471年期间与其他科学家的通信保存在纽伦堡市立图书馆。

内容来源：

<<Trigonometric Delights>> 作者：Eli Maor