原文链接：原文

梯度之上：Hessian 矩阵

本文讨论研究梯度下降法的一个有力的数学工具：海森矩阵。在讨论海森矩阵之前，需要首先了解梯度和雅克比矩阵的基本概念。

⭐️本文假设读者已经熟悉梯度下降法和简单的数值分析、线性代数知识

梯度、雅克比矩阵

梯度下降算法需要当前函数点的导数信息，当此函数点包含多个方向时，梯度是包含所有方向的（偏）导数向量。

上述情况对应于输出为一个的情况，当函数的输出也为一个向量时，我们需要把输出向量的每一个元素对于多个输入的梯度罗列在一起，罗列形成的矩阵就是雅克比矩阵（Jacobian Matrix）。

举例说明：

• 若函数$f$接受三个输入$x1、x2、x3$，产生一个输出$y$，则其梯度为：

$$\begin{array}{c}Grad=[\frac{\partial y}{\partial x_1},\frac{\partial y}{\partial x_2},\frac{\partial y}{\partial x_3}]\end{array}$$

• 若函数$f2$接受三个输入$x1、x2、x3$，产生三个输出$y1、y2、y3$，则其雅克比矩阵为：

$$\begin{array}{c}Jacobian=\left[\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}& \frac{\partial y_1}{\partial x_3}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}& \frac{\partial y_2}{\partial x_3}\\ \frac{\partial y_3}{\partial x_1}& \frac{\partial y_3}{\partial x_2}& \frac{\partial y_3}{\partial x_3}\end{array}\right]\end{array}$$

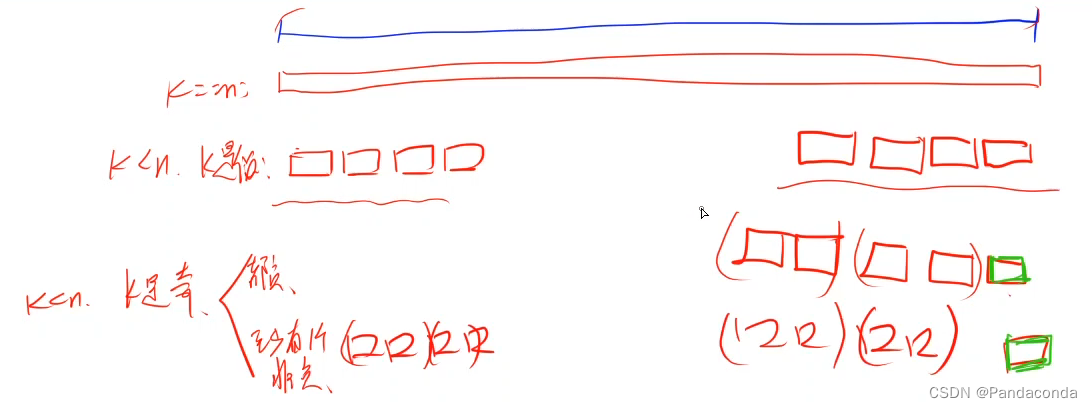
利用二阶导数，我们可以知道关于函数在特定方向 $d$ 上的凹凸信息，利用凹凸信息可以在一定程度上预判梯度下降法的表现效果。如果在特定方向 $d$ 上：

• 二阶导数为正，则函数在方向$d$上一阶导数增加，函数值下降更慢；

• 二阶导数为负，则函数在方向$d$上一阶导数减少，函数值下降更快；

• 二阶导数为零，则函数在方向$d$上一阶导数不变，函数值匀速下降；

  ⭐️注意在梯度下降法中是对损失函数进行下降，因此需要使用减函数来分析函数中某一小段（经常使用二次函数的减半部近似：二阶泰勒展开、牛顿法）中的导数变化情况；

海森矩阵

和雅克比矩阵类似，海森矩阵（Hessian 矩阵）可以包含函数中二阶导的信息：
$$Hessian=\left[\begin{array}{ccc}\frac{{\partial }^{2}y}{\partial x_1\partial x_1}& \frac{{\partial }^{2}y}{\partial x_1\partial x_2}& \frac{{\partial }^{2}y}{\partial x_1\partial x_3}\\ \frac{{\partial }^{2}y}{\partial x_2\partial x_1}& \frac{{\partial }^{2}y}{\partial x_2\partial x_2}& \frac{{\partial }^{2}y}{\partial x_2\partial x_3}\\ \frac{{\partial }^{2}y}{\partial x_3\partial x_1}& \frac{{\partial }^{2}y}{\partial x_3\partial x_2}& \frac{{\partial }^{2}y}{\partial x_3\partial x_3}\end{array}\right]$$
同时由于二阶导数计算顺序的可交换性，即 $\frac{{\partial }^{2}y}{\partial x_1\partial x_2}=\frac{{\partial }^{2}y}{\partial x_2\partial x_1}$，因此海森矩阵是一个对称矩阵，对于对称矩阵我们可以使用特征分解来研究特征值和二阶导数的关系，便于我们快速获得某个方向的二阶导数。

针对于特定方向d，已知此方向的二阶导数可以写成 $d^{T}Hd$ ，则：

🔗 基于Hessian矩阵的二阶方向导数与性质_Hi 喀什噶尔的胡杨的博客-CSDN博客_二阶方向导数

• 若d是H对应特征值λ的特征向量：

  因为d为对应λ的特征向量（以下简称特征向量），则据定义有：
  $$\begin{gathered} Hd=\lambda d \\ \Rightarrow d^{T}Hd=d^T\lambda d=\lambda d^{T}d=\lambda 对称矩阵d^T=d^{-} \end{gathered}$$

  因此特征向量对应的特征值λ即为此方向的二阶导数；

• 若d为其他方向：设$e_i$为$H$对应特征值${\lambda }_i$的特征向量，由上可知，
  $${\lambda }_i=e_i^{T}H{e}_i$$
  可知任何一个方向$d={\sum }_i^m{t}_i{e}_i$为特征向量的线性组合，其中m为特征值个数，$t_i$为第$i$个特征向量的加权数，则：
  $$d^{T}Hd=(\sum _i^m{t}_i{e}_i{)}^{T}H(\sum _i^m{t}_i{e}_i)=\sum _i^m{t}_i{e}_i^{T}H{t}_i{e}_i=\sum _i^m{t}_i^2{\lambda }_i$$
  因此任意非特征向量方向的二阶导数是所有特征值的加权和，特别的，此时的加权和是一个椭球体，在二维的特征值情况下，二阶导数是一个椭圆，椭圆方程为：
  $$y=\frac{{\lambda }_1}{\frac{1}{t_1^2}}+\frac{{\lambda }_2}{\frac{1}{t_2^2}}$$
  

  由图可知，最大二阶导数由最大特征值决定（长半轴），而最小二阶导数由最小特征值决定（短半轴）。

海森矩阵应用

在弄清海森矩阵的基本定义后，就可以使用海森矩阵的一些性质来分析优化方法中的一些问题了。如确定局部最大点、局部最小点和鞍点、确定学习率、以及使用病态条件来确定梯度下降的表现等，同时我们还可以利用Hessian矩阵来实现牛顿法这种优化算法，。

（本节完）