边界框回归（Bounding-Box Regression）

本篇博客实际上参考了CSDN另一篇博客写的 这是链接。但那篇博客的排版和语言表达实在是太烂了，公式错误也很多，以至于我花了很多时间才看明白。我将自己的思考结果记录下来，供大家参考。

一、边界框回归简介

那么边界框回归所要做的就是利用某种映射关系，使得候选目标框（region proposal）$P=\left(P_x,P_y,P_w,P_h\right)$的映射目标框无限接近于真实目标框（ground-truth）。将上述原理利用数学符号表示如下：在给定一组候选目标框 ，寻找到一个映射$f$ ，使得$f(P_x,P_y,P_w,P_h)=({\hat{G}}_x,{\hat{G}}_y,{\hat{G}}_w,{\hat{G}}_h)\approx \left(G_x,G_y,G_w,G_h\right)$ 。其中$\left(G_x,G_y,G_w,G_h\right)$表示真实值，$({\hat{G}}_x,{\hat{G}}_y,{\hat{G}}_w,{\hat{G}}_h)$表示预测值。

图1 边界框回归过程

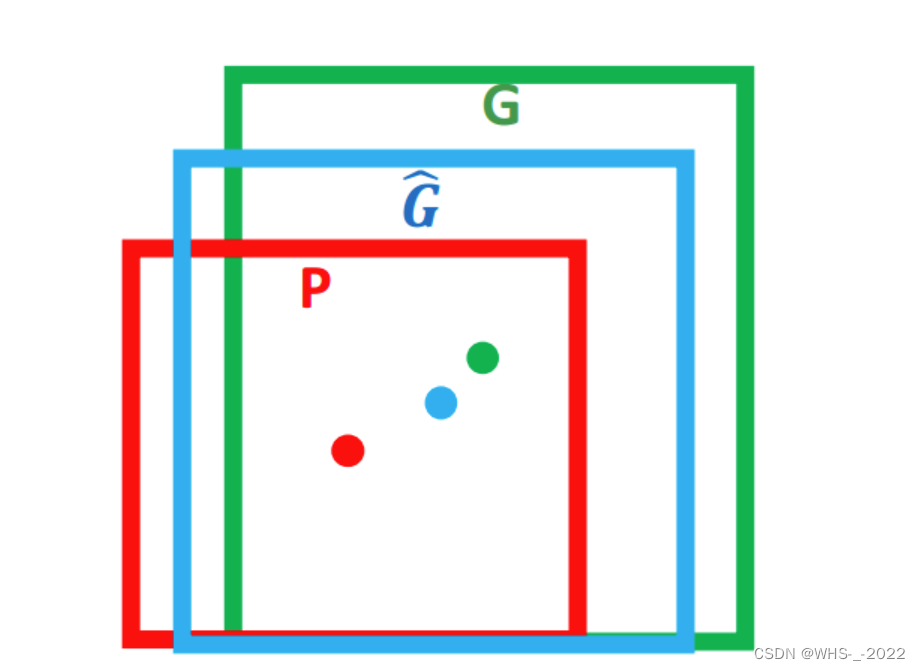
边界框回归过程图像表示如图1所示。在图1中红色框代表候选目标框，绿色框代表真实目标框，蓝色框代表边界框回归算法预测目标框。红色圆圈代表选候选目标框的中心点，绿色圆圈代表选真实目标框的中心点，蓝色圆圈代表选边界框回归算法预测目标框的中心点。

二、边界框回归细节

RCNN论文里指出，边界框回归是利用平移变换和尺度变换来实现映射 。平移变换的计算公式如下：
$$\{\begin{array}{l}{\hat{G}}_x=P_w{d}_x(P)+P_x\\ {\hat{G}}_y=P_h{d}_y(P)+P_y\end{array}\text{\hspace{1em}(1)}$$

尺度变换的计算公式如下：

$$\{\begin{array}{l}{\hat{G}}_w=P_w\exp \left(d_w(P)\right)\\ {\hat{G}}_h=P_h\exp \left(d_w(P)\right)\end{array}\text{\hspace{1em}(2)}$$
其中 $d_{\star }(P)$（$\star$代表$x,y,w,h$），是基于${\text{pool}}_5$的四个线性函数。在这里，我们将特征记作${\varphi }_5(P)$，那么$d_{\star }(P)=w_{\star }^T{\varphi }_5(P)$。因此，我们可以利用最小二乘法或者梯度下降算法进行求解 ，RCNN论文中给出了 的求解表达式：
$$w_{\ast }=\underset{{\hat{w}}_{\star }}{\mathrm{argmin}}\sum ^N{\left(t_{\ast }^i-{\hat{w}}_{\ast }^T{\varphi }_5\left(P^i\right)\right)}^2+\lambda {\Vert {\hat{w}}_{\ast }\Vert }^2\text{\hspace{1em}(3)}$$
其中：
$$\{\begin{array}{rl}{t}_x& =\frac{G_x-P_x}{P_w}\\ t_y& =\frac{G_y-P_y}{P_h}\\ t_w& =\log \frac{G_w}{P_w}\\ t_h& =\log \frac{G_h}{P_h}\end{array}\text{\hspace{1em}(4)}$$
$t_x$、$t_y$是中心点的平移移动，$t_w$、$t_h$是尺度放缩量。

可以看出，上述模型就是一个Ridge回归模型。在RCNN中，边界框回归要设计4个不同的Ridge回归模型分别求解 $w_x,w_y,w_w,w_h$ 。

回归模型的输入是什么？是$(P_x,P_y,P_w,P_h）$这个四维张量吗？

真正的输入是这个窗口对应的 CNN 特征，也就是 R-CNN 中的${\text{pool}}_5$（特征向量）。训练阶段也会用到Ground Truth的坐标数据，也就是式$(4)$提到的$t_{\star }$。

三、相关问题思考

1. 为什么使用相对坐标差?

在式$(4)$中 ，那么为什么要将真实框的中心坐标与候选框的中心坐标的差值分别除以宽高呢？

图2 尺寸不同的图片

接下来的讨论中，我们假设边界框的回归使用绝对坐标。

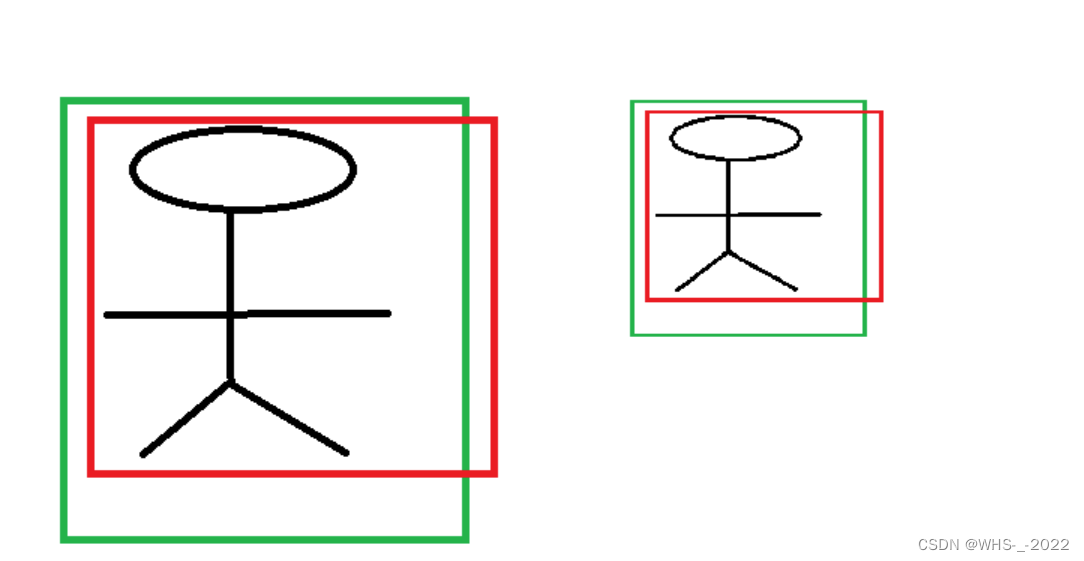
首先我们假设两张尺寸不同，但内容相同的图像，图像如图2所示。我们假设经过CNN提取的特征分别为${\varphi }_1$和${\varphi }_2$。同时，我们假设$x_i$为第$i$个真实目标框的$x$坐标， $p_i$为第$i$个候选目标框的$x$ 坐标，边界框回归$x$坐标的映射关系为$g_x$。那么我们可以得出：
$$\{\begin{array}{l}{g}_x\left({\varphi }_1\right)=x_1-p_1\\ g_x\left({\varphi }_2\right)=x_2-p_2\end{array}\text{\hspace{1em}(5)}$$
理论上来说，CNN得出的特征${\varphi }_1$和${\varphi }_2$是相似的，那么线性函数映射的结果也应该是接近的。但显然$x_1-p_1\ne x_2-p_2$。由于尺寸的变化，候选目标框和真实目标框坐标之间的偏移量也随着尺寸而成比例缩放，即这个值不是恒定不变的。但是归一化的比例值可以认为是近似相同的。

关于CNN是否有尺度不变性，这篇论文有说明过Object Detection in 20 Years: A Survey

因此，我们必须对$x$坐标的偏移量除以候选目标框的宽，$y$坐标的偏移量除以候选目标框的高。只有这样才能得到候选目标框与真实目标框之间坐标偏移量值的相对值。同时使用相对偏移量的好处可以自由选择输入图像的尺寸，使得模型灵活多变。也就说，对坐标偏移量除以宽高就是在做尺度归一化，即尺寸较大的目标框的坐标偏移量较大，尺寸较小的目标框的坐标偏移量较小。

2. 为什么宽高比要取对数?

类比问题1，我们不禁要问为什么不直接使用宽高的比值作为目标进行学习，非得“多此一举”取对数？

线性函数输出的是一个实数，因为宽和高乘的倍数必须大于0，所以要取指数的形式，反过来就是取对数。

3. 为什么IoU较大时边界框回归可视为线性变换？

‘Rich feature hierarchies for accurate object detection and semantic segmentation’文章中曾经提到，IoU必须大于$0.6$时，才可以使用线性回归，否则边界框回归将是一个复杂的非线性问题。

知乎上一篇博客曾经尝试解释过这个问题 这是链接。

但我觉得是不合理的，当$G_w\approx P_w$ 和$G_h\approx P_h$时候，式$(4)$的后两项确实可以视为某种线性的变换。但我们要理解到，我们回归的输入量是$(P_x,P_y,P_w,P_h)$窗口对应的 CNN 特征，而不是四维张量$(P_x,P_y,P_w,P_h)$。所以这里分析原边界框的坐标和Ground-truth的边界框坐标是否是线性关系是没有意义的。