文章目录
- 📚关系代数
- 🐇基本运算
- 🥕选择运算
- 🥕投影运算
- 🥕关系运算的组合
- 🥕集合并运算
- 🥕集合差运算
- 🥕集合交运算
- 🥕笛卡尔积运算
- 🥕更名运算
- 🥕一道综合例题
- 🐇附加运算
- 🥕自然连接运算
- 🥕赋值运算
- 🥕外连接运算
- 🐇扩展运算
- 🥕广义投影
- 🥕聚集运算
- 🥕除运算
- 📚元组关系演算
- 🐇概述
- 🐇元组关系演算查询示例
- 🐇形式化定义
- 🐇表达式的安全性
- 🐇运算符的优先次序
- 🐇等价性
- 🥕元组关系演算中的等价性
- 🥕元组关系演算与关系代数的等价性
- 📚域关系演算
- 🐇形式化定义
- 🐇查询事例
- 🐇表达式的安全性
- 📚习题练习
📚关系代数
🐇基本运算
🥕选择运算
- 选择运算选出满足给定谓词的元组。
- 我们用小写希腊字母
sigma(σ)来表示选择,而将谓词写作sigma的下标。参数关系在sigma后的括号中。 - 通常,我们允许在选择谓词中进行比较,使用的是
=,≠,<,≤等。另外,我们可以用连词将多个谓词合并成一个较大的谓词 - 示例:

🥕投影运算
- 投影运算是一元运算,它返回作为参数的关系,但把某些属性排除在外。由于关系是一个集合,所以所有重复行均被去除。
- 投影用大写希腊字母
pi表示,列举所以我们希望在结果中出现的属性作为pi的下标,作为参数的关系在跟随pi后的括号中 - 示例:

🥕关系运算的组合
- 关系运算的结果自身也是一个关系。一般来说,由于关系代数运算的结果同其输入的类型一样,所以我们可以把多个关系代数运算组合成为一个关系代数表达式
- 示例:

🥕集合并运算
- 要使运算
r∪s有意义,我们要求以下两个条件同时成立- 关系
r和s必须是同元的,即它们的属性数目必须相同 - 对所有的
i,r的第i个属性的域必须和s的第i个属性的域相同
域:属性的取值范围;r和s可以是数据库关系或者作为关系代数表达式结果的临时关系
- 关系
- 和集合论中的“并”运算一样用∪表示。由于关系是集合,所以重复值只留下了单个元组
- 示例:

🥕集合差运算
- 要使运算
r - s有意义,我们同样要求以下两个条件同时成立- 关系
r和s必须是同元的,即它们的属性数目必须相同 - 对所有的
i,r的第i个属性的域必须和s的第i个属性的域相同
- 关系
- 集合差运算使得我们可以找出在一个关系中而不在另一个关系中的那些元组。表达式
r - s的结果即一个包含所有在r中而不在s中的元组的关系 - 示例:

🥕集合交运算
- 要使运算
r n s有意义,我们同样要求以下两个条件同时成立- 关系
r和s必须是同元的,即它们的属性数目必须相同 - 对所有的
i,r的第i个属性的域必须和s的第i个属性的域相同
- 关系
r n s=r - (r-s)
🥕笛卡尔积运算
- 用
×表示的笛卡尔积运算使得我们可以将任意两个关系的信息组合在一起。
关系定义为一组域上的笛卡尔积的子集。
- 命名规则
- 规则①
- 由于相同的属性名可能同时出现在r1和r2中,所以采用的方法为找到属性所来自的关系,把关系名称附加到该属性上。
- 对那些只在两个关系模式之一中出现的属性,我们通常省略其关系名前缀,这样的简化不会用任何歧义。
- 这个命名规则规定作为笛卡尔积运算参数的关系名字必须不同。但这一规定存在问题,以下两个情况都将使用更名运算(具体见下一个胡萝卜)来避免这些问题:
- 🔑当某个关系需要与自身做笛卡尔积时;
- 🔑在笛卡尔积中使用关系代数表达式的结果时;
- 示例:

- 规则②
- 一般来说,如果有关系r1(R1)和r2(R2),则关系
r1×r2的模式是R1和R2串接而成的。关系R中包含所有满足以下条件的元组t:r1中存在元组t1且r2中存在元组t2,使得t[R1]=t1[R1]且t[R2]=t2[R2]
- 一般来说,如果有关系r1(R1)和r2(R2),则关系
- 规则①
- 示例:
- 假设我们希望找出物理系的所有教师,及其所教授的所有课程。为了实现这一要求,我们同时需要关系instructor和关系teaches中的信息。或许我们可以直接写成下面的表达式:
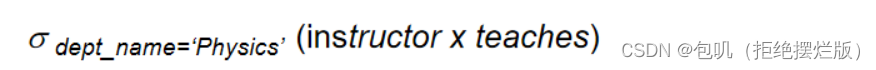
- 但是显然这样会造成一个结果,那就是最后所得的关系中包含物理系的教师,但course.id却可能包含除物理老师以外的老师教授的课程(因为笛卡尔积中保留了所有可能由一个来自instructor的元组和一个来自teaches的元组构成的元组对),如下表所示:
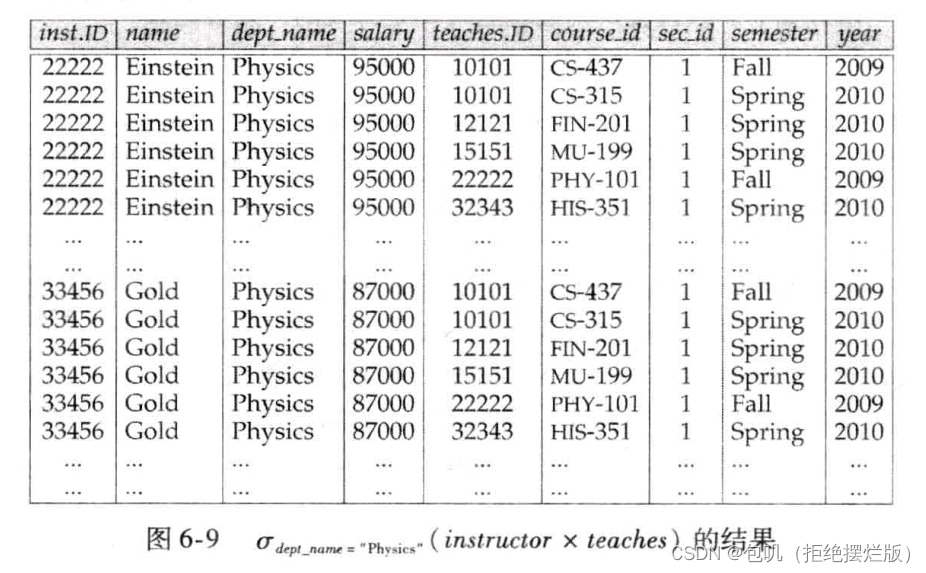
- 假设我们希望找出物理系的所有教师,及其所教授的所有课程。为了实现这一要求,我们同时需要关系instructor和关系teaches中的信息。或许我们可以直接写成下面的表达式:
- 显然表中只有
teaches.id=22222的课程才是Einstein物理老师教授的课程,剩下的课程是因为teaches关系串接而出现的,并不符合连接后对表的需求(instructor.id和teaches.id没有一一对应),因此我们用下面的表达式来纠正这个instructor.id和teaches.id不对应的问题

🥕更名运算
- 通过小写希腊字母
ρ表示更名运算。对于给定关系代数表达式E,表达式 ρ x ( E ) ρ_x(E) ρx(E) 返回表达式E的结果,并把名字x赋给了它- 允许我们命名或重新指定关系代数表达式的属性
- 允许我们给一个关系指定新的名字
- 单元表达式

- n元表达式
- 假设关系代数表达式E是n元的,则以下表达式返回表达式E的结果,并赋予它名字x,同时将各属性更名为A1,A2,…,An
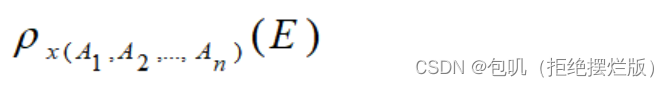
- 假设关系代数表达式E是n元的,则以下表达式返回表达式E的结果,并赋予它名字x,同时将各属性更名为A1,A2,…,An
🥕一道综合例题
查询“找出大学里的最高工资”
思路:最高工资 = 所有工资 - 除最高工资以外的工资
- 步骤一:计算笛卡尔积
instructor×instructor,区别好两个关系中的salary属性用于比较(为了无歧义的引用两次该属性,对第二个instructor关系使用更名运算,将其更名为关系d),然后比较这个笛卡尔积中两组salary属性值,选出除最高工资以外的工资(其原理是只要关系d中有salary比instructor大即可,是一个存在的全称量词——即存在salary属于d,大于salary属于instructor即可)
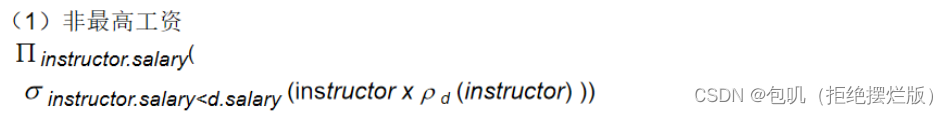
- 步骤二:所有工资减去除最高工资以外的工资即为最高工资,并进行投影运算

🐇附加运算
🥕自然连接运算
- 二元运算自然连接使得我们可以将某些选择和笛卡尔积运算合并为一个运算。我们用连接(join)符号来表示
- 自然连接运算首先形成它的两个参数的笛卡尔积,然后基于两个关系模式中都出现的属性上的相等性进行选择,最后还要去除重复性
- 它的便利性体现于自然连接运算只考虑在属性上值相同的元组对
- 自然连接的形式化定义

- 自然连接是可结合的
示例:找出计算机系的所有老师,以及他们教授的所有课程的名称
- 自然连接和笛卡尔积的联系
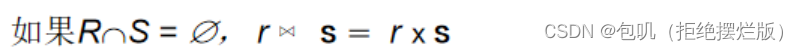
自然连接自动连接所有同名列,但如果两个关系没有同名列,就进行笛卡尔运算
- 自然连接扩展——theta连接,它使得我们可以把一个选择运算和一个笛卡尔积运算合并为单独的一个运算

🥕赋值运算
- 有时通过给临时关系变量赋值的方法来写关系代数表达式会很方便(可以理解为一种临时命名从而简化的操作)
- 赋值运算用
←表示,与程序语言中的赋值类似。使用赋值运算,我们可以把查询表达为一个顺序程序。 - 对关系代数查询而言,赋值必须是赋给一个临时关系变量。对永久关系的赋值形成了对数据库的修改。
- 例如:对自然连接从赋值运算的角度定义
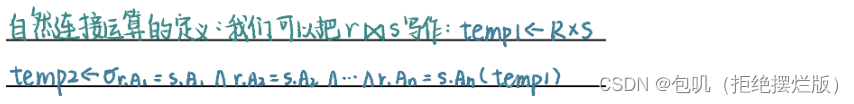
🥕外连接运算
扩展笔记——第四章:中级SQL,指路外连接,外连接的具体功能规则即sql规则,外连接运算可以用基本关系代数运算表示
-
外连接运算是连接运算的拓展,可以处理缺失的信息。一般地,参加连接的一个或两个关系中的某些元组可能因存在空值而“丢失”。外连接运算与自然连接运算相似,不同之处在于它在结果中创建带空值的元组,以此来保留在连接中丢失的那些元组。
-
左外连接

-
右外连接

-
全外连接

🐇扩展运算
🥕广义投影
- 广义投影允许在投影列表中使用算术运算和字符串函数等来对投影进行扩展

- 通常来说,在表达式中可以使用对数值属性或者产生数值结果的表达式的+、-、*、/等代数运算。广义投影还允许其他数据类型上的运算,比如对字符串的拼接。

🥕聚集运算
可以用来对值的集合使用聚集函数。
sum:求和&avg求平均&count计数&min/max求最小值最大值
- 聚集运算的通常形式

使用聚集函数对其进行操作的汇集中,一个值可以出现多次,值出现的顺序是无关紧要的,这样的汇集是多重集。集合是多重集的特例。
- 属性名更名用as子句

- 去重:用连字符将“distinct”附加在函数名后(如
count-distinct)
- 分组聚集

- 示例一

- 示例二

- 示例一
🥕除运算
除运算讲解补充优质博客
- 象集的定义
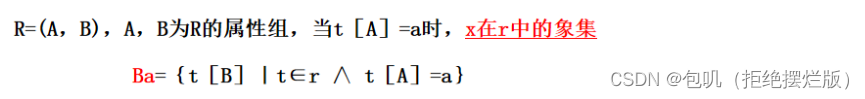
- 定义理解:R的属性任意分成两组A,B,任给值a, r中A部分等于a的行,在B上的投影形成一个象集。每个具体的a,都有一个象集,可能是空。
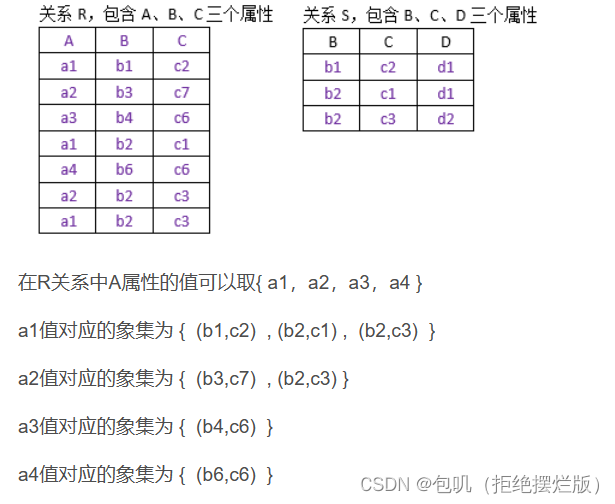
- 定义理解:R的属性任意分成两组A,B,任给值a, r中A部分等于a的行,在B上的投影形成一个象集。每个具体的a,都有一个象集,可能是空。
- 除运算定义

-
注意事项
(1)除运算是包含判断
(2)对语义“全部”、“所有”的处理
(3)除运算要凑准格式 -
示例
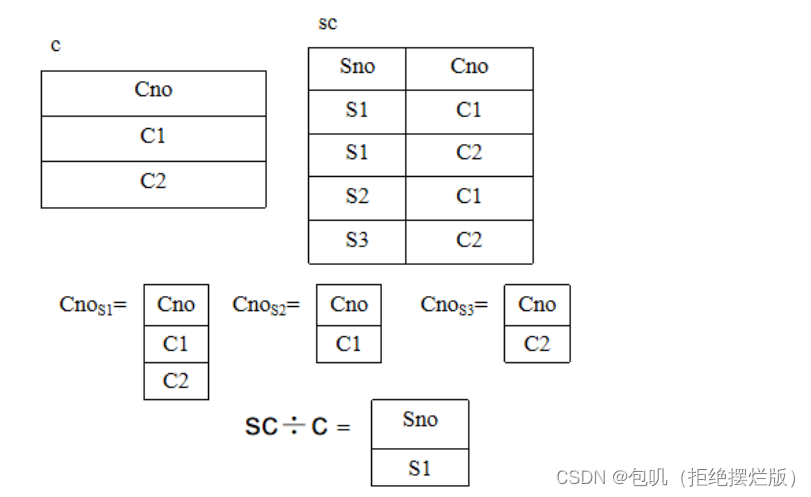
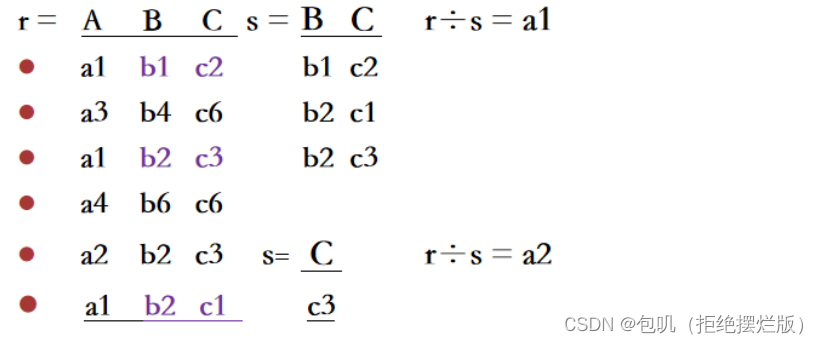
-
📚元组关系演算
🐇概述
-
元组关系演算是非过程化的查询语言。它只描述所需信息,而不给出获得该信息的具体过程。元组关系演算中的查询表达式为
{t|P(t)}它是所有使谓词P为真的元组t的集合
-
和前面的记法一样,我们用
t[A]表示元组t在属性A上的值,并用t∈r表示元组t在关系r中 -
∃ t∈r(Q(t))表示关系r中存在元组t使谓词Q(t)为真。常用于“假设我们只需要ID属性,而不是关系instructor的所有属性”这类要求
-
∀ t∈r(Q(t))表示对关系r中的所有元组t,Q均为真
-
🐇元组关系演算查询示例
-
查询找出工资大于80000美元的所有教师的ID

表达式解读
- 它是所有满足如下条件的元组t的集合:在关系instructor中存在元组s使t和s在属性ID上值相等,且s在属性salary上的值大于80000美元。
- 元组t只定义在ID属性上(相当于投影)
-
查询找出位置在Waston楼的系中的所有教师姓名

-
查询找出在2009年秋季学期或者2010年春季学期或者这两个学期都开设的所有课程的集合(集合并)

-
查询找出2009年秋季学期开设而2010年春季学期不开的所有课程

-
查询找出所有那些选了生物系全部课程的学生

表达式解读
- 全称量词
∀在这里表示,对关系course_id中所有的元组u,如果u在dept_name属性上的值是Biology,那么关系takes中一定存在一个包含该学生ID以及课程course_id的元组 - 特别注意

- 全称量词
🐇形式化定义
- 已知元组关系演算表达式为
{t | P(t) }, P是一个公式,公式中可以出现多个元组变量,如果元组变量不被∃或∀修饰,则称为自由变量

- 元组关系演算的公式由原子构成
- 原子的形式


- 原子的形式
🐇表达式的安全性
- 为了对元组关系演算进行限制,引入元组关系公式P的域(用dom§表示)这一概念。(它是P所引用的所有值的集合)
- 它们既包括P自身用到的值,又包括P中涉及的关系的元组中出现的所有值。因此,P的域是P中显式出现的值及名称出现在P中的那些关系的所有值的集合,公式的域,是值的集合,它不强调值“同类型”

🐇运算符的优先次序

🐇等价性
🥕元组关系演算中的等价性

🥕元组关系演算与关系代数的等价性

- 选择运算不用量词
- 投影运算用存在量词,属性名对应t,元组值对应存在量词后的字母
- 并、差、选择不用量词,投影、笛卡尔积用量词表示
- 量词是扫描一遍的意义,量词变量如同指针,依次定位在表中的各个元组上
📚域关系演算
🐇形式化定义
和元组关系演算同理

🐇查询事例
- 找出工资在80000美元以上的教师的ID、name、dept_name和salary
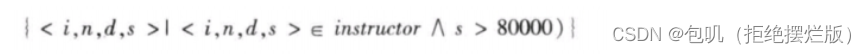
- 找出工资大于80000美元的所有教师的姓名

- 找出在物理系的所有教师姓名,以及他们教授的所有课程的course_id
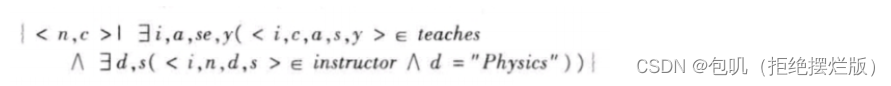
- 找出在2009年秋季学期或者2010年春季学期或者这两个学期都开设的所有课程的集合

- 找出选了生物系开设的全部课程的所有学生
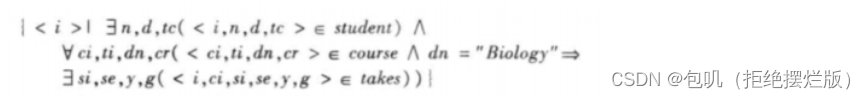
🐇表达式的安全性

📚习题练习

习题链接(含答案)




![LeetCode[547]省份数量](https://img-blog.csdnimg.cn/img_convert/819de989d4ff4cb798f1cb929a2ddb92.png)