摄像机

游戏中的相机可以理解为与现实中的相机类似，可以捕获对应的游戏画面。Camera在游戏引擎中一般也会展示为现实中相机的模型，使用时有两种实现方式，一种以组件形式挂载在Character上，一种则是单独存在。通常来讲，我们会对相机主体的位置和角度进行操作，以达到不同的设计目的。在本节中，我们来实现OpenGL中相机的创建。

一、观察空间（view space）

当我们讨论摄像机/观察空间(Camera/View Space)的时候，是在讨论以摄像机的视角作为场景原点时场景中所有的顶点坐标：观察矩阵把所有的世界坐标变换为相对于摄像机位置与方向的观察坐标，直观理解就是观察矩阵将摄像机移动到原点，并且把摄像机的坐标轴和世界坐标的坐标轴重合。

如何定义一个摄像机？需要定义下面的三个属性：

• 相机（眼睛）的位置（eye position） e
• 观察方向（gaze direction）g
• 视点正上方的方向（view-up vector）t

有了上面呢三个属性，我们便可以构建相机坐标系了：

首先先得到相机坐标系的 w 轴，对应标准坐标系下的 z 轴：

$w=\frac{-g}{||g||}$

然后通过向量 t 和 w 计算得到水平轴 u

$u=\frac{t\times w}{||t\times w||}$

最后将 w 和 u 叉乘得到坐标系的竖直分量 v

$v=\frac{w\times u}{||w\times u||}$

这里不直接用 **t **当作摄像机坐标系的竖直分量的原因是：我们的摄像机可能是歪着头看的，如下图，这个时候如果把 t 作为竖直坐标就错了。

有了相机空间坐标系，要如何把顶点从模型空间转化到相机空间呢？也就是我们的 view 矩阵要怎么得到呢？

• 将相机位置移动至原点
• 通过旋转矩阵将二者坐标系重合（将摄像机坐标旋转到世界坐标系）

这两个操作可能不是很好理解，试想将原本和标准坐标系重合的相机移动到现在坐标系的位置：先旋转和相机坐标系重合，然后移动到视点位置，对应的变换矩阵如下：

那么将摄像机和标准坐标系重合对应的矩阵为上述矩阵的逆矩阵：

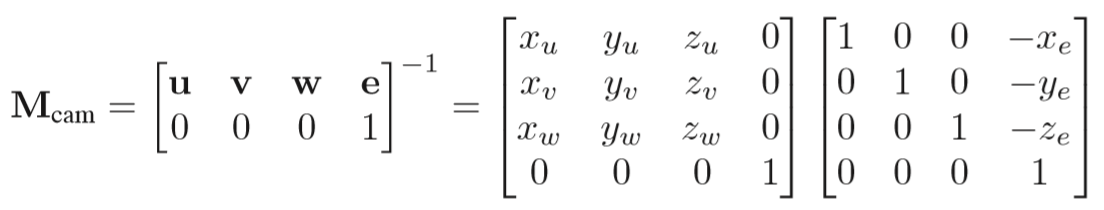
通过将转换到世界空间的坐标顶点左乘上述矩阵，则可以将顶点转化到相机空间中。

二、创建摄像机

首先先定义一个变量存储相机的位置，把摄像机位置设置为上一节中相同的位置：

	glm::vec3 camera_pos = glm::vec3(0.0f, 0.0f, 3.0f);

不要忘记正z轴是从屏幕指向你的，如果我们希望摄像机向后移动，我们就沿着z轴的正方向移动。

接着需要定义摄像机的观察方向和视点正上方的方向：

	glm::vec3 camera_target = glm::vec3(0.0f, 0.0f, 0.0f);
	glm::vec3 camera_direction = glm::normalize(camera_pos - camera_target);
	glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f);
	glm::vec3 camera_right = glm::cross(up, camera_direction);
	glm::vec3 camera_up = glm::cross(camera_direction, up);

glm 允许我们用 lookAt 函数来定义 view 矩阵：

//view
	glm::mat4 view = glm::lookAt(
		camera_pos, //position
		camera_pos + camera_front //target
		up //up
	);

glm::LookAt函数需要一个位置、目标和上向量。用该 view 矩阵替换我们之前创建的 view 矩阵，运行可以得到和之前相同的结果。

三、使相机动起来

现在我们想让相机围着场景中的物体旋转，保持 y 坐标不动，让 x 和 z 坐标沿着一个圆心为原点的圆旋转：

首先回想一下极坐标的转换公式：

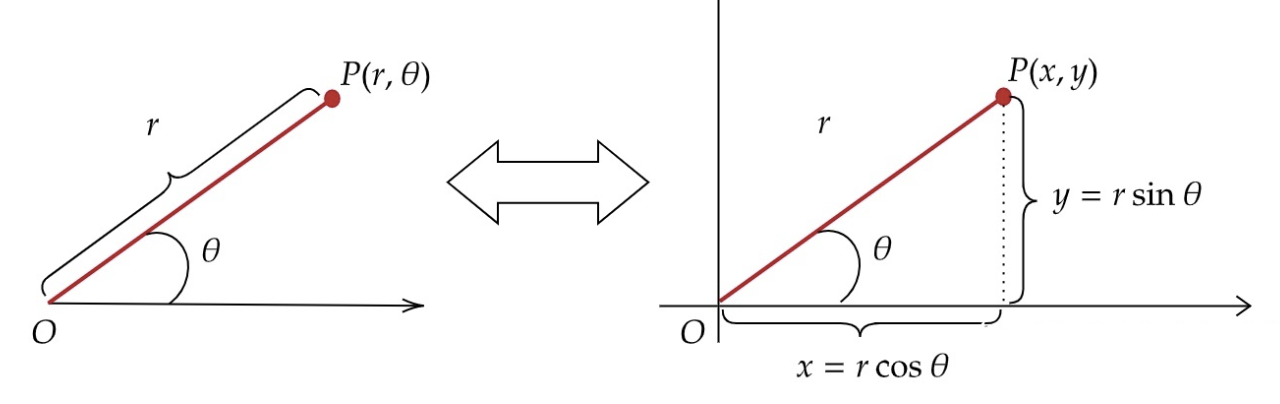
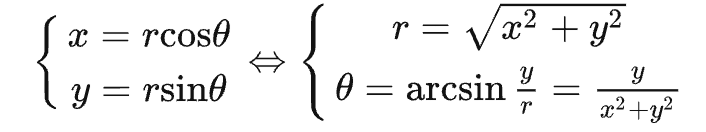
这里我们使用时间变量作为 $\theta$ 来改变相机的 x 坐标和 z 坐标：

		float radius = 10.0f;
		camera_pos.x = cos(time_value) * radius; //x = r.sin(theta)
		camera_pos.z = sin(time_value) * radius; //z = r.cos(theta)
		camera_front = glm::vec3(0.0f, 0.0f, 0.0f) - camera_pos;


		view = glm::lookAt(
			camera_pos, //position
			camera_pos + camera_front, //target
			up //up
		);

如果一切正常，你会得到如下的结果：

四、通过键盘输入控制相机移动

如果想使用键盘控制相机的移动，首先要做的是将我们上面定义的相机属性定义为全局变量：

static glm::vec3 camera_pos = glm::vec3(0.0f, 0.0f, 3.0f);
static glm::vec3 camera_front = glm::vec3(0.0f, 0.0f, -1.0f);
static glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f);

用这三个变量在渲染循环中来构造我们的 view 矩阵：

	view = glm::lookAt(
			camera_pos, //position
			camera_pos + camera_front, //target
			up //up
		);

检查下能不能正常观察到物体：

然后，在之前实现的 process_input 函数中，添加用于控制相机的代码：

//camera controller
	float camera_speed = 0.05f;
	if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS)
		camera_pos += camera_speed * glm::normalize(camera_front);
	if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS)
		camera_pos -= camera_speed * glm::normalize(camera_front);
	if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS)
		camera_pos -= camera_speed * glm::normalize(glm::cross(camera_front, up));
	if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS)
		camera_pos += camera_speed * glm::normalize(glm::cross(camera_front, up));

其中定义了控制相机移动速度的变量 camera_speed ，要注意的是，实际情况下根据处理器的能力不同，有些人可能会比其他人每秒绘制更多帧，也就是以更高的频率调用process_input函数，所以即使设定相同的相机速度，在不同电脑上的运行速度也可能不一样，因此需要根据我们自己的电脑手动进行调整。

当我们按下WASD键的任意一个，摄像机的位置都会相应更新。如果我们希望向前或向后移动，我们就把位置向量加上或减去方向向量。如果我们希望向左右移动，我们使用叉乘来创建一个右向量(Right Vector)，并沿着它相应移动就可以了。这样就创建了使用摄像机时熟悉的横移(Strafe)效果。

注意，右向量需要进行标准化。如果没对这个向量进行标准化，最后的叉乘结果会根据camera_front返回大小不同的向量。如果我们不对向量进行标准化，我们就得根据摄像机的朝向不同加速或减速移动了，但如果进行了标准化移动就是匀速的。

五、Delta Time

TimeStep 实现的原理主要是计算并记录当前帧和上一帧之间经历的时长，然后通过这个间隔来控制我们将照相机或者物体移动时候的速度。虽然不同机器执行一次Loop函数的用时不同，但只要把每一帧里的运动，跟该帧所经历的时间相乘，就能抵消因为帧率导致的数据不一致的问题。

我们使用变量 delta_time来跟踪每一帧运行所需要的时间，用last_frame 来跟踪上一帧的时间，创建全局变量：

//delta time
static float delta_time = 0.0f;
static float last_frame = 0.0f;

然后在渲染循环中更新这两个变量：

//update delta time
		float current_frame = (float)glfwGetTime();
		delta_time = current_frame - last_frame;
		last_frame = current_frame;

最后给 camera_speed 加上这个 delta_time，这样，当两帧之间时间较长的时候，会以更快的速度进行移动来弥补，这样有了一个在任何系统上移动速度都一样的摄像机。

六、添加视角移动：

就像一般的FPS游戏一样，我们通过鼠标移动来控制视角的移动，我们之前定义的 camera_front 变量，就可以改变相机的视点朝向，所以我们通过鼠标的输入来完成对 camera_front 的旋转即可控制视角移动。

6.1 欧拉角

来简单复习一下欧拉角，欧拉角是我们使用旋转时候较为简单的一种方式。

==欧拉角(Euler Angle)==是可以表示3D空间中任何旋转的3个值，由莱昂哈德·欧拉(Leonhard Euler)在18世纪提出。一共有3种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)，下面的图片展示了它们的含义：

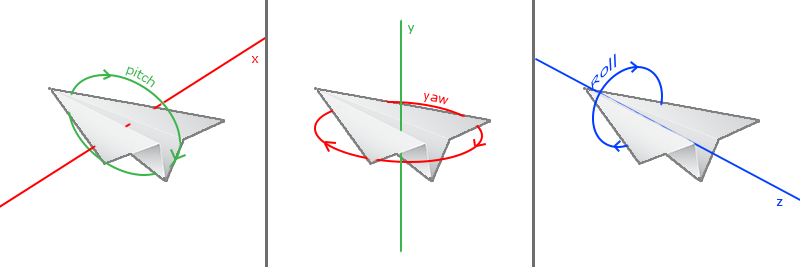
俯仰角是描述我们如何往上或往下看的角，一般情况下是沿着 x 轴旋转。偏航角表示往左和往右看的程度，一般是沿着 y 轴旋转。滚转角代表如何翻滚摄像机，通常在太空飞船的摄像机中使用。每个欧拉角都有一个值来表示，把三个角结合起来就能够计算3D空间中任何的旋转向量了。

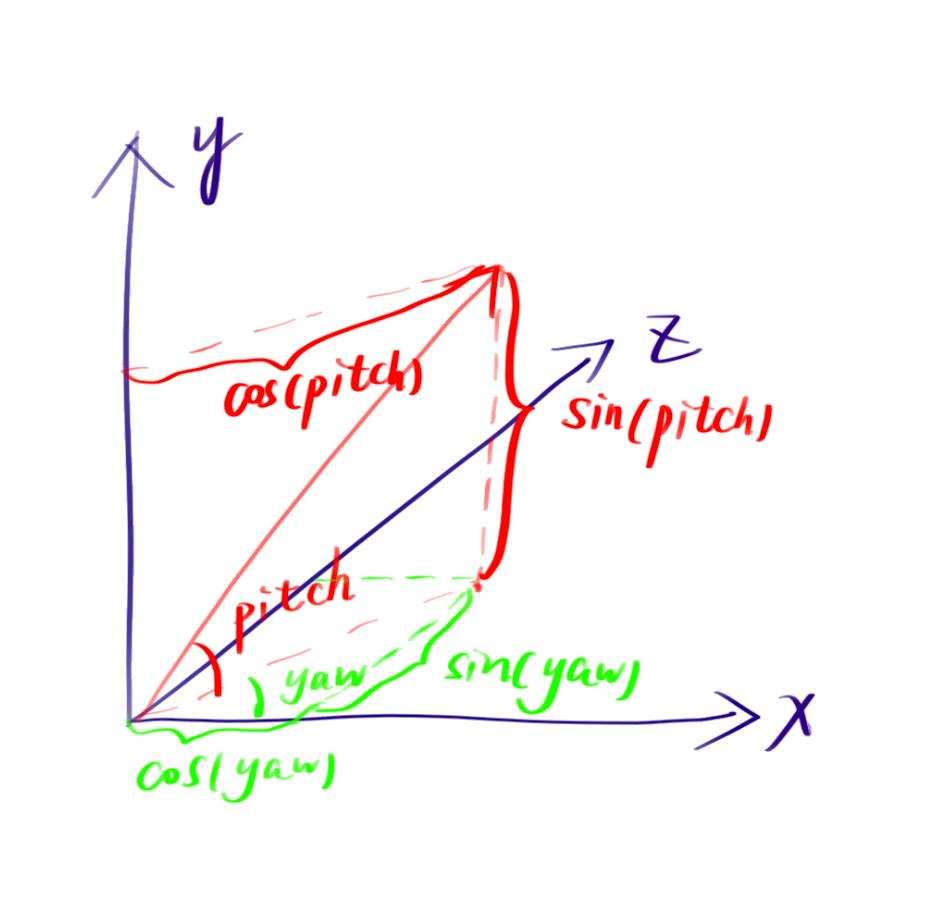
如上图所示，对于空间中的某个向量，代表了我们当前相机的朝向，我们假设其为 direction ，其坐标按照如图所示的方法求：

direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw)); 
direction.y = sin(glm::radians(pitch));
direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));

6.2 鼠标输入

我们通过检测鼠标的输入来进行偏航角和俯仰角的设置，水平移动影响偏航角，竖直移动影响俯仰角。原理就是，储存上一帧鼠标的位置，在当前帧中我们当前计算鼠标位置与上一帧的位置相差多少。如果水平/竖直差别越大那么俯仰角或偏航角就改变越大，也就是摄像机需要移动更多的距离。

首先隐藏鼠标的光标，并聚焦到当前窗口上，通过函数 glfwSetInputMode：

glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_DISABLED);

接着创建监听鼠标移动事件的回调函数，在此之前，先使用GLFW注册回调函数：

glfwSetCursorPosCallback(window, mouse_callback);

回调函数如下：

void mouse_callback(GLFWwindow* window, double x_pos, double y_pos)
{
	float x_offset = x_pos - last_x;
	float y_offset = last_y - y_pos; // 这里是相反的，因为y是从下向上增加，而 pitch 从下向上减小
	last_x = x_pos;
	last_y = y_pos;

	float sensitivity = 0.005f;//根据实际运动速度调节
	x_offset *= sensitivity;
	y_offset *= sensitivity;

	yaw += x_offset;
	pitch += y_offset;
	//never make pitch >= 90.f 
	if (pitch > 89.0f)
		pitch = 89.0f;
	if (pitch < -89.0f)
		pitch = -89.0f;

	glm::vec3 front;
	front.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw));
	front.y = sin(glm::radians(pitch));
	front.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));
	camera_front = glm::normalize(front);

}

窗口第一次获取焦点的时候摄像机会突然跳一下。这个问题产生的原因是，在你的鼠标移动进窗口的那一刻，鼠标回调函数就会被调用，这时候的xpos和ypos会等于鼠标刚刚进入屏幕的那个位置。这通常是一个距离屏幕中心很远的地方，因而产生一个很大的偏移量，所以就会跳了。我们可以简单的使用一个bool变量检验我们是否是第一次获取鼠标输入，如果为true，那么我们先把鼠标的初始位置更新为xpos和ypos值，接下来的鼠标移动就会使用刚进入的鼠标位置坐标来计算偏移量了：

if (first_mouse)
	{
		last_x = x_pos;
		last_y = y_pos;
		first_mouse = false;
	}

然后来设置通过鼠标滚轮控制缩放，视野(Field of View)或fov定义了我们可以看到场景中多大的范围。当视野变小时，场景投影出来的空间就会减小，产生放大(Zoom In)了的感觉。

鼠标滚轮的回调函数如下：

void scroll_callback(GLFWwindow* window, double x_offset, double y_offset)
{
	if (fov >= 1.0f && fov <= 45.0f)
		fov -= y_offset;
	if (fov < 1.0f)
		fov = 1.0f;
	if (fov > 45.0f)
		fov = 45.0f;
}

然后我们在每一帧中更新我们的 projection 矩阵：

		projection = glm::perspective(glm::radians(fov), (float)screen_width / (float)screen_height, 0.1f, 100.0f);

注册回调函数：

glfwSetScrollCallback(window, scroll_callback);

现在可以运行查看结果了。

（视频太大这里就不放了，可以自己运行查看效果）