Linux C编程一站式学习笔记 chap5 深入理解函数
文章目录
嘶,大一时的C语言学的时候确实没有总结过这个return,当时也木有学那个增量式开发
一.return语句
-
在有返回值的函数中,
return语句的作用是提供整个函数的返回值,并结束当前函数返回到调用它的地方 -
在没有返回值的函数中也可以使用return语句,例如当检查到一个错误时提前结束当前函数的执行并返回:
#include <math.h> void print_logarithm(double x) { if (x <= 0.0) { printf("Positive numbers only, please.\n"); return; } printf("The log of x is %f", log(x)); }这个函数首先检查参数
x是否大于0,如果x不大于0就打印错误提示,然后提前结束函数的执行返回到调用者,只有当x大于0时才能求对数,在打印了对数结果之后到达函数体的末尾,自然地结束执行并返回。注意,使用数学函数log需要包含头文件math.h,由于x是浮点数,应该与同类型的数做比较,所以写成0.0
逻辑与运算符在C语言中写成两个&号(Ampersand)
C语言还提供了逻辑或(Logical OR)运算符,写成两个|线(Pipe Sign)
逻辑非(Logical NOT)运算符,写成一个!号(Exclamation Mark)
在编程语言中表示真和假的数据类型叫做布尔类型,在C语言中通常用
int型来表示,非0表示真,0表示假
-
例:返回布尔值的检查奇偶性的函数
int is_even(int x) { if( x%2 == 0) return 1; else return 0; }写成return(1);这种形式也可以,表达式外面套括号表示改变运算符优先级,在这里不起作用
返回布尔值的函数是一类非常有用的函数,在程序中通常充当控制表达式,函数名通常带有
is或if等表示判断的词,这类函数也叫做谓词(Predicate)我们可以调用这个函数,比如下面这种写法
int i = 19; if (is_even(i)) { /* do something */ } else { /* do some other thing */ } -
我们可以简化一下刚刚那个
is_even函数,x % 2这个表达式本来就有0值或非0值,直接把这个值当作布尔值返回就可以了int is_even(int x) { return !( x % 2); } -
函数的返回值可以这样理解:
函数返回一个值相当于定义一个和返回值类型相同的临时变量,并用return后面的表达式来初始化
例如上面的函数调用相当于这样的过程:
int 临时变量 = !(x % 2); 函数退出,局部变量x的存储空间释放; if (临时变量) { /* 临时变量用完就释放 */ /* do something */ } else { /* do some other thing */ }当
if语句对函数的返回值做判断时,函数已经退出,局部变量x已经释放,所以不可能在这时候才计算表达式!(x % 2)的值,表达式的值必然是事先计算好了存在一个临时变量里的,然后函数退出,局部变量释放,if语句对这个临时变量的值做判断。 -
注意,虽然函数的返回值可以看作是一个临时变量,但我们只是读一下它的值,读完值就释放它,而不能往它里面存新的值,换句话说,函数的返回值不是左值,或者说函数调用表达式不能做左值,因此下面的赋值语句是非法的:
is_even(20) = 1; xxx返回值也是按值传递(call by value)的,即便返回语句写成
return x;,返回的也是变量x的值,而非变量x本身,因为变量x马上就要被释放了。
习题
1、编写一个布尔函数int is_leap_year(int year),判断参数year是不是闰年。如果某年份能被4整除,但不能被100整除,那么这一年就是闰年,此外,能被400整除的年份也是闰年。
int is_leap_year(int year)
{
if( year % 4 == 0 && year % 100 !=0 || year % 400 == 0)
return 1;
else
return 0;
}
2、编写一个函数double myround(double x),输入一个小数,将它四舍五入。例如myround(-3.51)的值是-4.0,myround(4.49)的值是4.0。可以调用math.h中的库函数ceil和floor实现这个函数。
-
一开始写的
double myround(double x) { if( x * 100 % 100 >= 50) { return ceil(x); } else { return floor(x); } }vscode 和 pythontutor都报了这个错误,看来有点想当然了…
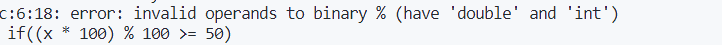

-
这个应该是可以的👇
#include <math.h> double myround(double x) { if (x >= 0) { return floor(x + 0.5); } else { return ceil(x - 0.5); } }
二.增量式开发
这节主要讲的是一种编程思维吧
- 这一节讲的太棒了!
- 值得反复回看!!!
- http://akaedu.github.io/book/ch05s02.html
- 从初学者的视角以一个简单的例子引入,命中了很多痛点,让人读完恍然大悟, 很多曾经试过的方法作为一时的经验已经遗忘了, 但读完这节发现那些方法是可以进入思维体系的!
- 此外,这个对于写博客也很有启发,真的写的很通俗易懂且有趣,最重要的是有代入感!
三.递归
-
如果定义一个概念需要用到这个概念本身,我们称它的定义是递归的(Recursive)
-
数学上的阶乘(factorial)就是用它自己来定义的:n的阶乘等于n乘以n-1的阶乘
-
n-1的阶乘是什么?是n-1乘以n-2的阶乘。那n-2的阶乘又是什么?这样下去永远也没完。因此需要定义一个最关键的基础条件(Base Case):0的阶乘等于1
0! = 1 n! = n*(n-1)!
-
-
下面我们来用code完成这个简单的计算过程
-
先把Base Case写进去
int factorial(int n) { if(n==0) return 1; } -
如果参数n不是0,该return什么呢?
-
应该
return n*factorial(n-1) -
为了下面的分析方便,我们引入几个临时变量把这个语句拆分一下:
int factorial(int n) { if(n==0) return 1; else { int recurse = factorial(n-1); int result = n * recurse; return result; } }factorial这个函数居然可以自己调用自己?是的。自己直接或间接调用自己的函数称为递归函数
-
-
-
这里的factorial是直接调用自己,有些时候函数A调用函数B,函数B又调用函数A,也就是函数A间接调用自己,这也是递归函数。
-
可以把factorial(n-1)这一步看成是在调用另一个函数:另一个有着相同函数名和相同代码的函数,调用它就是跳到它的代码里执行,然后再返回factorial(n-1)这个调用的下一步继续执行。我们以factorial(3)为例分析整个调用过程,如下图所示:

图中用实线箭头表示调用,用虚线箭头表示返回,右侧的框表示在调用和返回过程中各层函数调用的存储空间变化情况
main()有一个局部变量result,用一个框表示- 调用
factorial(3)时要分配参数和局部变量的存储空间,于是在main()的下面又多了一个框表示factorial(3)的参数和局部变量,其中n已初始化为3 factorial(3)又调用factorial(2),又要分配factorial(2)的参数和局部变量,于是在main()和factorial(3)下面又多了一个框。每次调用函数时分配参数和局部变量的存储空间,退出函数时释放它们的存储空间。factorial(3)和factorial(2)是两次不同的调用,factorial(3)的参数n和factorial(2)的参数n各有各的存储单元,虽然我们写代码时只写了一次参数n,但运行时却是两个不同的参数n。并且由于调用factorial(2)时factorial(3)还没退出,所以两个函数调用的参数n同时存在,所以在原来的基础上多画一个框。- 依此类推,请读者对照着图自己分析整个调用过程。读者会发现这个过程和前面我们用数学公式计算3!的过程是一样的,都是先一步步展开然后再一步步收回去。
我们看上图右侧存储空间的变化过程,随着函数调用的层层深入,存储空间的一端逐渐增长,然后随着函数调用的层层返回,存储空间的这一端又逐渐缩短,并且每次访问参数和局部变量时只能访问这一端的存储单元,而不能访问内部的存储单元,比如当factorial(2)的存储空间位于末端时,只能访问它的参数和局部变量,而不能访问factorial(3)和main()的参数和局部变量。具有这种性质的数据结构称为堆栈或栈(Stack),随着函数调用和返回而不断变化的这一端称为栈顶,每个函数调用的参数和局部变量的存储空间(上图的每个小方框)称为一个栈帧(Stack Frame)。
操作系统为程序的运行预留了一块栈空间,函数调用时就在这个栈空间里分配栈帧,函数返回时就释放栈帧。
-
写递归函数时一定要记得写Base Case,否则即使递推关系正确,整个函数也不正确。如果
factorial函数漏掉了Base Case:int factorial(int n) { int recurse = factorial(n-1); int result = n * recurse; return result; }那么这个函数就会永远调用下去,直到操作系统为程序预留的栈空间耗尽程序崩溃(段错误)为止,这称为无穷递归(Infinite recursion)
-
递归不只是为解决数学题[8]而想出来的招,它是计算机的精髓所在,也是编程语言的精髓所在
-
其实expression和statement也是递归定义的
-
expression
表达式 → 表达式(参数列表) 参数列表 → 表达式, 表达式, ... -
statement
语句 → if (控制表达式) 语句
-
-
-
递归和循环其实是等价的
- 这一节写的也精彩,又渗透了很多编程思想,还推荐了很多经典书籍,如SICP,编译原理龙书等
- 值得反复回看:http://akaedu.github.io/book/ch05s03.html
我猜有递归可视化工具,一搜果真有收获
-
Data Structure Visualizations这个网站里面有
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZUt0Oknb-1674408367332)(null)]
-
https://recursion.vercel.app/这个体验也很棒
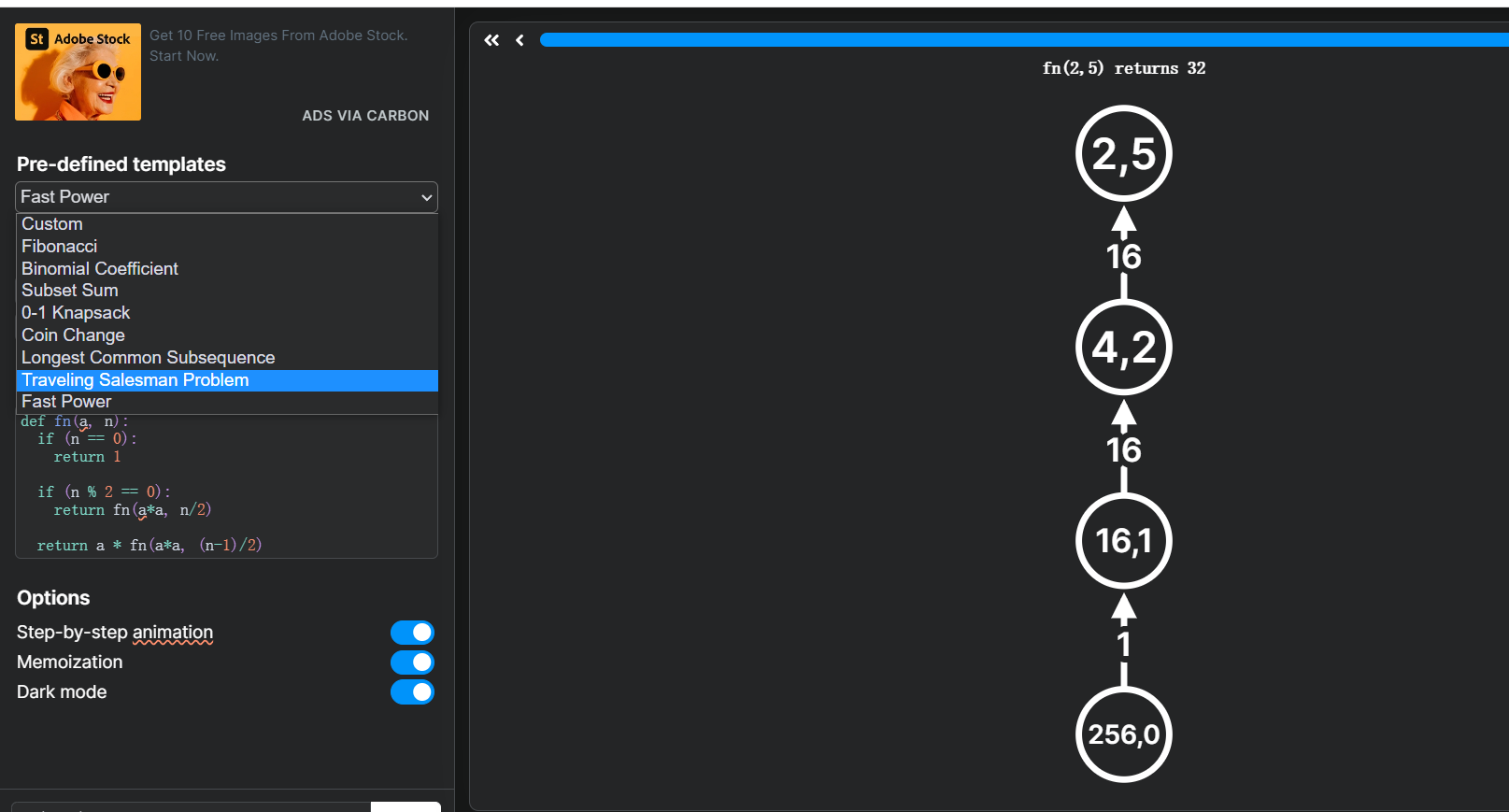
去广告版:https://quanticdev.com/tools/recursion-visualization/
- GitHub链接:https://github.com/brpapa/recursion-tree-visualizer
-
visualgo网站:
https://visualgo.net/en/recursion
-
python turtle可以实现可视化
- https://runestone.academy/ns/books/published/pythonds3/Recursion/VisualizingRecursion.html
习题
GCD(Greatest Common Divisor) 最大公约数
1、编写递归函数求两个正整数a和b的最大公约数(GCD,Greatest Common Divisor),使用Euclid(欧几里得)算法: 如果a除以b能整除,则最大公约数是b。 否则,最大公约数等于b和a%b的最大公约数。
int gcd(int a, int b)
{
if( a % b == 0)
return b;
else
return gcd(b, a%b)
}
Fibonacci
2、编写递归函数求Fibonacci数列的第n项,这个数列是这样定义的:
fib(0)=1
fib(1)=1
fib(n)=fib(n-1)+fib(n-2)
int fibonacci(int n)
{
if( n == 0 || n == 1)
return 1;
else
return fibonacci(0) + fibonacci(1);
}
相关资源、参考资料
-
豆瓣评价
-
开源电子书
-
《Linux C编程一站式学习》这书写得很不错,为什么都买不到了呢? - echo1937的回答 - 知乎 https://www.zhihu.com/question/34069391/answer/544825938
-
[大佬们的学习笔记]
- 习题答案整理
-
https://blog.csdn.net/weixin_44576779/article/details/87443584
-
echo1937的回答 - 知乎 https://www.zhihu.com/question/34069391/answer/544825938




![线性代数[向量]](https://img-blog.csdnimg.cn/35d8c6f2c260420296d2c546a1a08336.png)