系列文章目录
第一章 线性代数[初等变换(一)]
第二章 线性代数[初等变换(二)]
第三章 线性代数[初等变换(三)]
第四章 线性代数[矩阵的秩]
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
前言
一.引入
二.向量的概念和运算
三.线性相关
四.与秩的关系
五.定理
前言
今天大概内容:
今天浅浅的讲解一下线性代数中最抽象的一节内容《向量》
提示:以下是本篇文章正文内容,下面案例可供参考
一.引入
有了前面行列式和矩阵这两个话题的铺垫,可以让线性代数的主人翁一向量出场了.前面指出,矩阵中的若干个行(列)都是向量,它们之间存在着某种联系,这种联系说到底就是线性无关的向量个数(独立信息的个数)的问题,也就是若千个向量组成的向量组中,其中某几个就足够代表这个向量组了,其他的向量都可以由这几个向量线性表示出来.比如,向量组[1,2,3],[6,7,9]与[2.4,6],有三个成员,其他的向量都可以由这几个向量线性表示出来.比如,向量组[1,2,3],[6,7,9]与[2.4,6],有三个成员,其他的向量都可以由这几个向量线性表示出来.比如,向量组[1,2,3],[6,7,9]与[2.4,6],有三个成员,其他的向量都可以由这几个向量线性表示出来.比如,向量组[1,2,3],[6,7,9]与[2.4,6],有三个成员,
给大家举个例子如图:

有的同学会问为什么?
二.向量的概念和运算
n维向量: n 个数构成的一-个有序数组[a1,a2....an.]称为有一个n维向量,记成a=[a1,a2..an.],并
称a为n维行向量,aT= [a1,a2,..,an]T称为n维列向量,其中a;称为向量a(或aT)[aT是转置]的第i个分量.
相等: 若a=[a1,a2.....an].b= [b1,b2,...,bn]都是n维向量,则当且仅当ai,=bi(i= 1.2...n),a=b.
加法: a+b=[a1+b1,a2+b2,..........,an+bn](a,b同上)
数乘: ka=[ka1,ka2......kan](a同上,k为实数)
三.线性相关
线性相关:对于向量a1,a2....am,如存在一组不全为零的数k1,k2......km使用线性组合
k1a1+k2a2+......+kma1m=0
则称向量组a1,a2......am线性代数相关,否则称它线性无关.
证明:
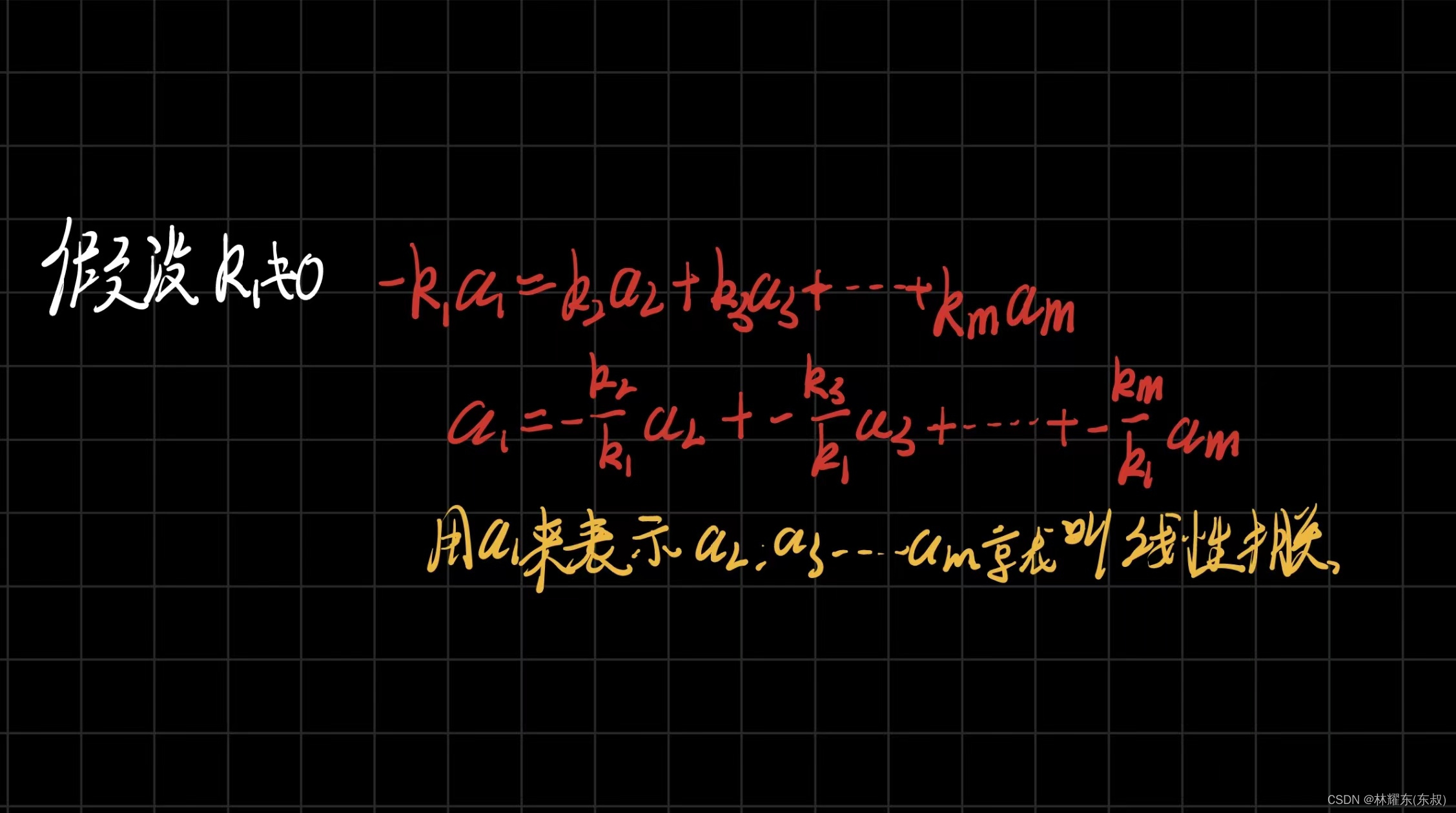
就像上面的[1,2,3],[6,7,9]与[2.4,6],有三个成员
就像[1,2,3]可以替换[2,4,6]出现这种情况就可以称之为线性相关
四.与秩的关系
定理向量组 A:a1a2...,am线性相关的充分必要条件是它所构成的矩阵A=(a1,a2,..am )的秩小于向量个数m;向量组A线性无关的充分必要条件是R(A)=m.

所以说除定理可以判断线性相关也可以使用秩来判断
五.定理