题目描述

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 105
0 <= prices[i] <= 104

求解思路

1. 该题目通过动态规划来求解，首先我们先来思考的就是状态怎么表示，通过题目的意思我们可以知道，有买入和售出俩种状态，我们可以遍历整个过程，通过中间的状态转移来求解最终的结果
2. 当前手上没有股票可能有俩种结果，第一种是之前就没买，第二种是之前买了，但是现在卖了
3. 当前手上有股票也有俩种结果，第一种就是之前买了，第二种就是现在刚买
4. 通过上面的求解求解，我们就可以求解最终结果，最后我们直接返回就可以了。

实现代码

class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        int[][] dp=new int[n][2];
        dp[0][0]=0;
        dp[0][1]=-prices[0];
        for(int i=1;i<n;i++){
            dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
            dp[i][1]=Math.max(dp[i-1][1],-prices[i]);
        }
        return dp[n-1][0];
    }
}

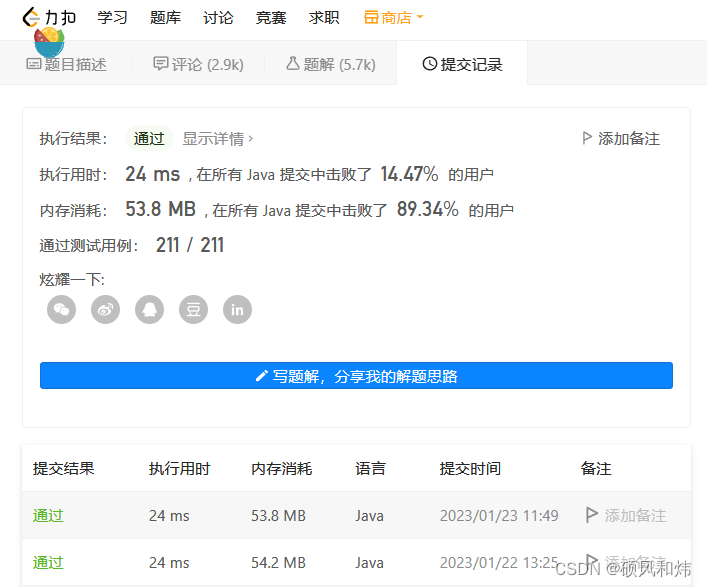
运行结果