✍个人博客：https://blog.csdn.net/Newin2020?spm=1011.2415.3001.5343
📚专栏地址：蓝桥杯题解集合
📝原题地址：等差数列
📣专栏定位：为想参加蓝桥杯的小伙伴整理常考算法题解，祝大家都能取得理想成绩！
❤️如果有收获的话，欢迎点赞👍收藏📁，您的支持就是我创作的最大动力💪

问题描述

数学老师给小明出了一道等差数列求和的题目。

但是粗心的小明忘记了一部分的数列，只记得其中 N 个整数。

现在给出这 N 个整数，小明想知道包含这 N 个整数的最短的等差数列有几项？

输入格式

输入的第一行包含一个整数 N。

第二行包含 N 个整数 A1,A2,⋅⋅⋅,AN。(注意 A1∼AN 并不一定是按等差数
列中的顺序给出)

输出格式

输出一个整数表示答案。

数据范围

2≤N≤100000,
0≤Ai≤10⁹

输入样例：

5
2 6 4 10 20

输出样例：

10

样例解释

包含 2、6、4、10、20 的最短的等差数列是 2、4、6、8、10、12、14、16、18、20。

思路

由于给定的数在同一个等差数列中，所以一定有公式 $(a_{末}-a_{首})/d+1$，其中 $a_{末}$ 和 $a_{首}$ 分别为给定数列的最大值和最小值，d 为数列的公差。

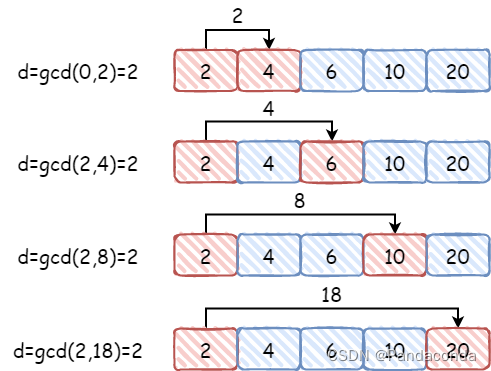
如果想要使结果尽可能的小，则 d 要尽可能的大，所以 d 取其他数与最小数的差值的最大公约数。举个例子，这个序列可能是 $a_0+a_1+a_2+a_3+a_4=a_0+(a_0+d)+(a_0+3d)+(a_0+5d)+(a_0+7d)$，则 d 就要取 0、d、3d、5d、7d 的最大公约数使公式值最小即项数最少。

代码

#include<bits/stdc++.h>
using namespace std;

const int N = 100010;
int a[N];
int n;

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i++)    scanf("%d", &a[i]);
    sort(a, a + n);	//一定要排序

    //计算最大公约数
    int d = 0;
    for (int i = 1; i < n; i++)    d = gcd(d, a[i] - a[0]);

    //输出最小项数
    if (!d)  printf("%d\n", n);
    else    printf("%d\n", (a[n - 1] - a[0]) / d + 1);

    return 0;
}