[python刷题模板] 树的直径/换根DP
- 一、 算法&数据结构
- 1. 描述
- 2. 复杂度分析
- 3. 常见应用
- 4. 常用优化
- 二、 模板代码
- 1. 单纯询问树的直径值
- 2. 求出树的直径两端搞事情
- 3. 换根DP求树的直径(大炮打蚊子,别这么做,只是用来帮助理解换根DP)
- 4. 换根dp求特定值(另附小日子模板)
- 5. 换根dp求去掉一个叶子的值。
- 三、其他
- 四、更多例题
- 五、参考链接
一、 算法&数据结构
1. 描述
树的直径代表树上最远的两个点的距离。
在某些特定的时候会用到。
- 求树的直径通常可以
- 树形DP:仅用来计算直径的值,一次dfs即可。由于直径一定是某个子树的两个连接根的最长简单路径拼起来(其中一个可能是空),因此令dfs(u)计算u的子树树高(最长路径),计算v时,同时维护v的兄弟节点最大那个,每次都加一下尝试更新答案即可。
- 两次遍历(bfs/dfs均可):可以同时计算直径的值且找到两个端点。第一次遍历从任意一点root找最远节点u,第二次从u出发,找最远节点v,u和v就是直径的两端。
- 换根DP(大炮打蚊子):进用来计算直径的值,假设直径两端是u,v,那么以u为树根,v一定是最远节点,求最大树高即可。
换根DP是一种树上DP,可以用O(n)的复杂度计算出:分别以每个节点作为整个树的树根,树的某个属性值(如:树高)。
之所以把换根dp和树的直径写在一起,是因为,求树的直径时不论是树形dp还是换根DP,都可以结合着思考更容易吃透。
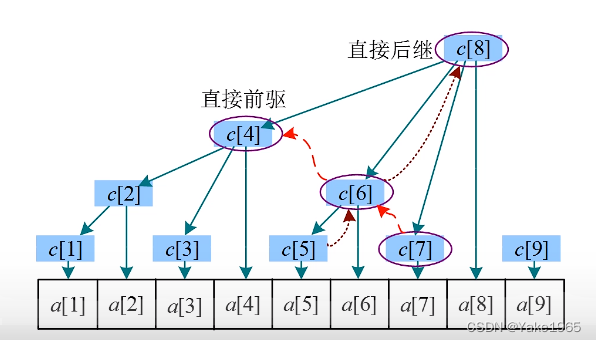
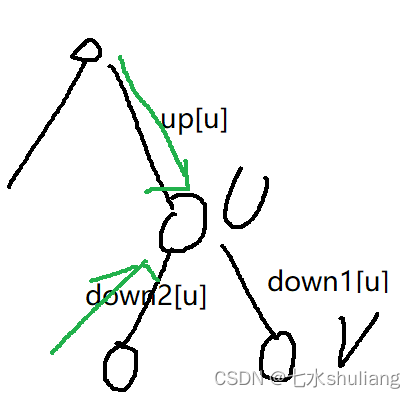
- 记录三个数组down1,down2,up,分别表示:
- down1[u]: 以u为根的子树,向下最大的值(比如求树高,就是最长简单路径)
- down2[u]: 以u为根的子树,向下次大的值(比如求树高,就是最长简单路径)
- up[u]: 以u为根的子树,向上最大的值(比如求树高,就是最长简单路径)
- 那么当
整颗树以u为根时,最大值就是max(down1[u],up[u])。可以想象一下揪着u节点往上提,所有路径其实就是down和up。 - 第一遍dfs,后根遍历求出down1和down2。
- 第二遍dfs,先根遍历求出up,注意讨论:如果当前节点v在u的最大路径(down1)下,up[v]应该从应该从u的次大(down2[u])来,或up[u]来,见途中绿色轨迹;否则从最大来。
2. 复杂度分析
- O(ln)
3. 常见应用
4. 常用优化
- 换根DP的三个数组,可以写成f = [[0,0,0] for _ in range(n)],但这是负优化,还是写三个好使。
- 换根DP可以用BFS先列出dp序,然后遍历,省去dfs爆栈的开销。
二、 模板代码
1. 单纯询问树的直径值
例题: 4799. 最远距离
这题是一道裸的树的直径。下边的代码大部分会用这题测试。
- 如果没特殊需求,建议用两次bfs免去爆栈风险。
def bootstrap(f, stack=[]):
def wrappedfunc(*args, **kwargs):
if stack:
return f(*args, **kwargs)
else:
to = f(*args, **kwargs)
while True:
if type(to) is GeneratorType:
stack.append(to)
to = next(to)
else:
stack.pop()
if not stack:
break
to = stack[-1].send(to)
return to
return wrappedfunc
# 4994 ms
def solve2():
n, m = RI()
g = [[] for _ in range(n)]
for _ in range(m):
u, v = RI()
g[u - 1].append(v - 1)
g[v - 1].append(u - 1)
start = 0
ans = 0
for _ in range(2):
@bootstrap
def dfs(u, fa, depth=0):
nonlocal ans, start
if depth > ans:
start = u
ans = depth
for v in g[u]:
if v != fa:
yield dfs(v, u, depth + 1)
yield
dfs(start, -1)
print(ans)
# 3618 ms
def solve1():
n, m = RI()
g = [[] for _ in range(n)]
for _ in range(m):
u, v = RI()
g[u - 1].append(v - 1)
g[v - 1].append(u - 1)
start = 0
ans = 0
for _ in range(2):
q = deque([start])
fas = [-1] * n
step = 0
while q:
step += 1
for _ in range(len(q)):
u = q.popleft()
start = u
for v in g[u]:
fas[v] = u
if v != fas[u]:
q.append(v)
ans = max(ans, step)
print(ans - 1)
2. 求出树的直径两端搞事情
链接: abc267_f - Exactly K Steps
- 这题找出一条直径,就是最大支持的距离,如果够就可以。
- 因此还需要多一次dfs,记录当前路径。
- 方便的写法就是三次dfs,前两次找直径,第三次算答案,每次都记录最远的端点作为下一次的起始点即可。
bfs找直径模板
def get_tree_diameter(g, root=0): # bfs两次找直径的端点
"""
求树的直径,g是0-indexed,默认第一次root是从0
返回某条直径的两个端点u,v,以及直径值d(边数而不是点数)
简述:求树的直径时,可以通过树形DP做,也可以通过两次遍历找最远的点(bfs或dfs都可以)
第二次的起始点就是某条直径的端点
"""
if not g[root]:
return root, root, 0
def bfs(start):
q = deque([(start, -1)])
step = -1
while q:
step += 1
for _ in range(len(q)):
u, fa = q.popleft()
for v in g[u]:
if v != fa:
q.append((v, u))
return u, step
x, _ = bfs(root)
y, d = bfs(x)
return x, y, d
ac代码
import sys
import heapq
import bisect
import random
import io, os
from bisect import *
from collections import *
from contextlib import redirect_stdout
from itertools import *
from math import sqrt, gcd, inf
from array import *
from functools import lru_cache
from types import GeneratorType
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
MOD = 10 ** 9 + 7
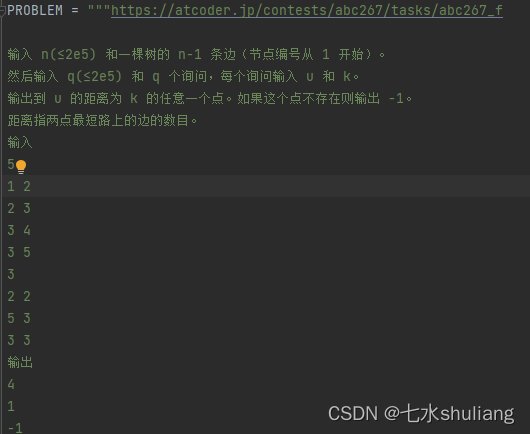
PROBLEM = """https://atcoder.jp/contests/abc267/tasks/abc267_f
输入 n(≤2e5) 和一棵树的 n-1 条边(节点编号从 1 开始)。
然后输入 q(≤2e5) 和 q 个询问,每个询问输入 u 和 k。
输出到 u 的距离为 k 的任意一个点。如果这个点不存在则输出 -1。
距离指两点最短路上的边的数目。
输入
5
1 2
2 3
3 4
3 5
3
2 2
5 3
3 3
输出
4
1
-1
"""
"""https://atcoder.jp/contests/abc267/submissions/37595672
求出树的任意一条直径,设直径端点为 x 和 y。
从 x 出发 dfs,同时记录 dfs 路径上的点。
如果点 u 的深度 d >= k,那么 dfs 路径上的第 d-k 个点就是答案。
一次 dfs 不一定能满足所有点,再从 y 出发 dfs 一次就能保证所有点都有答案(除了 k 非常大的)。
"""
def bootstrap(f, stack=[]):
def wrappedfunc(*args, **kwargs):
if stack:
return f(*args, **kwargs)
else:
to = f(*args, **kwargs)
while True:
if type(to) is GeneratorType:
stack.append(to)
to = next(to)
else:
stack.pop()
if not stack:
break
to = stack[-1].send(to)
return to
return wrappedfunc
# 1629 ms
if __name__ == '__main__':
n, = RI()
g = [[] for _ in range(n)]
for _ in range(n - 1):
u, v = RI()
g[u - 1].append(v - 1)
g[v - 1].append(u - 1)
q, = RI()
qs = defaultdict(list)
for i in range(q):
u, d = RI()
qs[u - 1].append([i, d])
ans = [-1] * q
leaf = mx = 0
path = [-1] * n
@bootstrap
def dfs(u, fa, d=0):
path[d] = u
global leaf, mx
if d > mx:
leaf = u
mx = d
for i, k in qs[u]:
if d >= k:
ans[i] = path[d - k] + 1
for v in g[u]:
if v != fa:
yield dfs(v, u, d + 1)
yield
for _ in range(3):
dfs(leaf, -1)
print('\n'.join(map(str, ans)))
# # 1423 ms
# if __name__ == '__main__':
# n, = RI()
# g = [[] for _ in range(n)]
# for _ in range(n - 1):
# u, v = RI()
# g[u - 1].append(v - 1)
# g[v - 1].append(u - 1)
#
#
# def get_tree_diameter(g, root=0): # bfs两次找直径的端点
# if not g[root]:
# return root, root
#
# def bfs(start):
# q = deque([(start, -1)])
# while q:
# u, fa = q.popleft()
# for v in g[u]:
# if v != fa:
# q.append((v, u))
# return u
#
# x = bfs(root)
# y = bfs(x)
# return x, y
#
#
# x, y = get_tree_diameter(g)
#
# q, = RI()
# qs = defaultdict(list)
# for i in range(q):
# u, d = RI()
# qs[u - 1].append([i, d])
# # print(qs)
# ans = [-1] * q
# path = [0] * n # 当前深度链接到根的路径
#
#
# @bootstrap
# def dfs(u, fa, d=0):
# path[d] = u
# for i, k in qs[u]:
# if d >= k:
# ans[i] = path[d - k] + 1
# for v in g[u]:
# if v != fa:
# yield dfs(v, u, d + 1)
# yield
#
#
# dfs(x, -1)
# dfs(y, -1)
# print('\n'.join(map(str, ans)))
# # 1892ms
# if __name__ == '__main__':
# n, = RI()
# g = [[] for _ in range(n)]
# for _ in range(n - 1):
# u, v = RI()
# g[u - 1].append(v - 1)
# g[v - 1].append(u - 1)
#
#
# def get_tree_diameter(g, root=0):
# ans = (0, root, root)
# if not g[root]:
# return ans
#
# dp = {}
#
# @bootstrap
# def dfs(u, fa, depth=0): # 返回树高以及最深的叶子
# if len(g[u]) == 1 and u != root: # 没有子节点了,它就是一个端点(叶子),高度1
# dp[u] = (1, u)
# yield
#
# hs = []
# for v in g[u]:
# if v != fa:
# yield dfs(v, u, depth + 1)
# h, o = dp[v]
# if len(hs) < 2:
# heapq.heappush(hs, (h, o))
# else:
# heapq.heappushpop(hs, (h, o))
#
# if len(hs) == 2:
# l, r = max((depth, root), hs[0]), hs[1]
# else:
# l, r = (depth, root), hs[0]
# p = (l[0] + r[0], l[1], r[1])
# # print(p)
# nonlocal ans
# if p > ans:
# ans = p
# dp[u] = (hs[-1][0] + 1, hs[-1][1])
# yield
#
# dfs(root, -1)
# return ans
#
#
# d, x, y = get_tree_diameter(g)
#
# q, = RI()
# qs = defaultdict(list)
# for i in range(q):
# u, d = RI()
# qs[u - 1].append([i, d])
# # print(qs)
# ans = [-1] * q
# path = [0] * n # 当前深度链接到根的路径
#
#
# @bootstrap
# def dfs(u, fa, d=0):
# path[d] = u
# for i, k in qs[u]:
# if d >= k:
# ans[i] = path[d - k] + 1
# for v in g[u]:
# if v != fa:
# yield dfs(v, u, d + 1)
# yield
#
#
# dfs(x, -1)
# dfs(y, -1)
# print('\n'.join(map(str, ans)))
3. 换根DP求树的直径(大炮打蚊子,别这么做,只是用来帮助理解换根DP)
# 换根dp 4122 ms
def solve():
n, m = RI()
g = [[] for _ in range(n)]
for _ in range(m):
u, v = RI()
g[u - 1].append(v - 1)
g[v - 1].append(u - 1)
def get_tree_diameter(g, root=0): # bfs两次找直径的端点
""" ms
求树的直径,g是0-indexed,默认第一次root是从0
返回直径值(边数而不是点数)
简述:换根dp,假设直径两端是u,v,那么以u为树根,v一定是最远节点,求最大树高即可。
"""
if not g[root]:
return 0
down1, down2, up = [0] * n, [0] * n, [0] * n # 初始化向下最大/次大树高、向上树高(其实不是树高,是最远简单路径)
order = [] # dp序
fas = [-1] * n # 记录父节点
q = deque([root]) # bfs求order
while q:
u = q.popleft()
order.append(u)
for v in g[u]:
if v != fas[u]:
fas[v] = u
q.append(v)
for u in order[::-1]: # 第一遍,自底向上求每个子树的最大/次大树高
for v in g[u]:
if v == fas[u]:
continue
h = down1[v] + 1 # 高度
if h > down1[u]:
down1[u], down2[u] = h, down1[u]
elif h > down2[u]:
down2[u] = h
for u in order:
for v in g[u]:
if v == fas[u]:
continue
if down1[u] == down1[v] + 1: # v在u的最大路径上,则往上的路径应该可能从次大走
up[v] = max(down2[u], up[u]) + 1
else: # 否则一定从最大走
up[v] = max(down1[u], up[u]) + 1
return max(max(x, y) for x, y in zip(down1, up))
print(get_tree_diameter(g))
4. 换根dp求特定值(另附小日子模板)
链接: abc222_f - Expensive Expense
- 这题由于要附加一个路径上的端点节点值,因此更新答案时多了个,可能是d[u]+w。
- solve2/3分别是用上述方法三个数组down1/2+up计算的过程。
- 另附一个从周赛抄来的模板,我尽可能的按照自己的理解把注释写成了中文。
- 模板需要调整三个地方 e/op/composition方法,具体可以看代码。
- 注意e通常是0,我目前做的题都是。
- op目前我做的题都是max。
- composition是最关键的,知道子树和节点,如何拼接答案。
# Problem: F - Expensive Expense
# Contest: AtCoder - Exawizards Programming Contest 2021(AtCoder Beginner Contest 222)
# URL: https://atcoder.jp/contests/abc222/tasks/abc222_f
# Memory Limit: 1024 MB
# Time Limit: 4000 ms
import sys
import bisect
import random
import io, os
from bisect import *
from collections import *
from contextlib import redirect_stdout
from itertools import *
from math import sqrt, gcd, inf
from array import *
from functools import lru_cache
from types import GeneratorType
from heapq import *
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
MOD = 10 ** 9 + 7
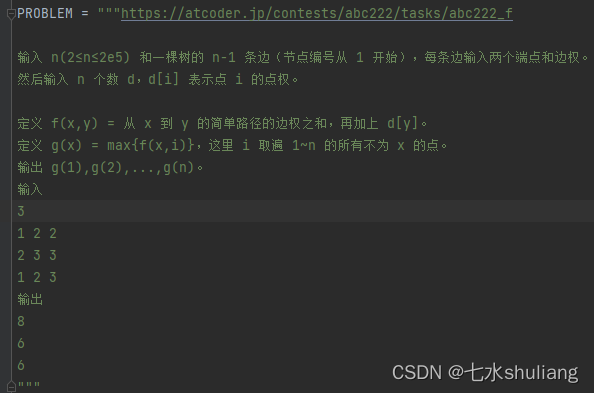
PROBLEM = """https://atcoder.jp/contests/abc222/tasks/abc222_f
输入 n(2≤n≤2e5) 和一棵树的 n-1 条边(节点编号从 1 开始),每条边输入两个端点和边权。
然后输入 n 个数 d,d[i] 表示点 i 的点权。
定义 f(x,y) = 从 x 到 y 的简单路径的边权之和,再加上 d[y]。
定义 g(x) = max{f(x,i)},这里 i 取遍 1~n 的所有不为 x 的点。
输出 g(1),g(2),...,g(n)。
输入
3
1 2 2
2 3 3
1 2 3
输出
8
6
6
"""
from typing import Callable, Generic, List, TypeVar
T = TypeVar("T")
E = Callable[[int], T]
"""identify element of op, and answer of leaf"""
Op = Callable[[T, T], T]
"""merge value of child node"""
Composition = Callable[[T, int, int, int], T]
"""return value from child node to parent node"""
# 1187 ms
def solve():
class Rerooting(Generic[T]):
__slots__ = ("g", "_n", "_decrement", "_root", "_parent", "_order")
def __init__(self, n: int, decrement: int = 0, edges=None):
"""
n: 节点个数
decrement: 节点id可能需要偏移 (1-indexed则-1, 0-indexed则0)
"""
self.g = g = [[] for _ in range(n)]
self._n = n
self._decrement = decrement
self._root = None # 一开始的根
if edges:
for u, v in edges:
u -= decrement
v -= decrement
g[u].append(v)
g[v].append(u)
def add_edge(self, u: int, v: int):
"""
无向树加边
"""
u -= self._decrement
v -= self._decrement
self.g[u].append(v)
self.g[v].append(u)
def rerooting(
self, e: E["T"], op: Op["T"], composition: Composition["T"], root=0
) -> List["T"]:
"""
- e: 初始化每个节点的价值
(root) -> res
mergeの単位元
例:求最长路径 e=0
- op: 两个子树答案如何组合或取舍
(childRes1,childRes2) -> newRes
例:求最长路径 return max(childRes1,childRes2)
- composition: 知道子子树答案和节点值,如何更新子树答案
(from_res,fa,u,use_fa) -> new_res
use_fa: 0表示用u更新fa的dp1,1表示用fa更新u的dp2
例:最长路径return from_res+1
- root: 可能要设置初始根,默认是0
<概要> 换根DP模板,用线性时间获取以每个节点为根整颗树的情况。
注意最终返回的dp[u]代表以u为根时,u的所有子树的最优情况(不包括u节点本身),因此如果要整颗子树情况,还要再额外计算。
1. 记录dp1,dp2。其中:
dp1[u] 代表 以u为根的子树,它的孩子子树的最优值,即u节点本身不参与计算。注意,和我们一般定义的f[u]代表以u为根的子树2情况不同。
dp2[v] 代表 除了v以外,它的兄弟子树的最优值。依然注意,v不参与,同时u也不参与(u是v的父节点)。
建议画图理解。
2. dp2[v]的含义后边将进行一次变动,变更为v的兄弟、u的父过来的路径,merge上u节点本身最后得出来的值。即v以父亲为邻居向外延伸的最优值(不含v,但含父)。
3. 同时dp1[u]的含义更新为目标的含义:以u为根,u的子节点们所在子树的最优情况。
4. 这样dp1,dp2将分别代表u的向下子树的最优,u除了向下子树以外的最优(一定从父节点来,但父节点可能从兄弟来或祖宗来)
<步骤>
1. 先从任意root出发(一般是0),获取bfs层序。这里是为了方便dp,或者直接dfs树形DP其实也是可以的,但可能会爆栈。
2. 自底向上dp,用自身子树情况更新dp1,除自己外的兄弟子树情况更新dp2。
3. 自顶向下dp,变更dp2和dp1的含义。这时对于u来说存在三种子树(强烈建议画图观察):
① u本身的子树,它们的最优解已经存在于之前的dp1[u]。
② u的兄弟子树+fa,它们的最优解=composition(dp2[u],fa,u,use_fa=1)。
③ 连接到fa的最优子树+fa,最优解=composition(dp2[fa],fa,u,use_fa=1)。
注意这里的dp2含义已变更,由于我们是自顶向下计算,因此dp2[fa]已更新。
②和③可以写一起来更新dp2[u]
計算量 O(|V|) (Vは頂点数)
参照 https://qiita.com/keymoon/items/2a52f1b0fb7ef67fb89e
"""
# step1
root -= self._decrement
assert 0 <= root < self._n
self._root = root
g = self.g
_fas = self._parent = [-1] * self._n # 记录每个节点的父节点
_order = self._order = [root] # bfs记录遍历层序,便于后续dp
q = deque([root])
while q:
u = q.popleft()
for v in g[u]:
if v == _fas[u]:
continue
_fas[v] = u
_order.append(v)
q.append(v)
# step2
dp1 = [e(i) for i in range(self._n)] # !子树部分的dp值,假设u是当前子树的根,vs是第一层儿子(它的非父邻居),则dp1[u]=op(dp1(vs))
dp2 = [e(i) for i in
range(
self._n)] # !非子树部分的dp值,假设u是当前子树的根,vs={v1,v2..vi..}是第一层儿子(它的非父邻居),则dp2[vi]=op(dp1(vs-vi)),即他的兄弟们
for u in _order[::-1]: # 从下往上拓扑序dp
res = e(u)
for v in g[u]:
if _fas[u] == v:
continue
dp2[v] = res
res = op(res, composition(dp1[v], u, v, 0)) # op从下往上更新dp1
# 由于最大可能在后边,因此还得倒序来一遍
res = e(u)
for v in g[u][::-1]:
if _fas[u] == v:
continue
dp2[v] = op(res, dp2[v])
res = op(res, composition(dp1[v], u, v, 0))
dp1[u] = res
# step3 自顶向下计算每个节点作为根时的dp1,dp2的含义变更为:dp2[u]为u的兄弟+父。这样对v来说dp1[u] = op(dp1[fa],dp1[u])
for u in _order[1:]:
fa = _fas[u]
dp2[u] = composition(
op(dp2[u], dp2[fa]), fa, u, 1
) # op从上往下更新dp2
dp1[u] = op(dp1[u], dp2[u])
return dp1
n, = RI()
r = Rerooting(n)
ws = {}
for _ in range(n - 1):
u, v, w = RI()
u -= 1
v -= 1
ws[u, v] = w
ws[v, u] = w
r.add_edge(u, v)
d = RILST()
def e(root: int) -> int:
# 转移时单个点不管相邻子树的贡献
# 例:最も遠い点までの距離を求める場合 e=0
return 0
def op(child_res1: int, child_res2: int) -> int:
# 如何组合/取舍两个子树的答案
# 例:求最长路径 return max(childRes1,childRes2)
return max(child_res1, child_res2)
def composition(from_res: int, fa: int, u: int, use_fa: int = 0) -> int:
# 知道子树的每个子树和节点值,如何更新子树答案;
# 例子:求最长路径 return from_res+1
if use_fa == 0: # cur -> parent
return max(from_res, d[u]) + ws[u, fa]
return max(from_res, d[fa]) + ws[fa, u]
res = r.rerooting(e, op, composition)
print(*res, sep='\n')
def bootstrap(f, stack=[]):
def wrappedfunc(*args, **kwargs):
if stack:
return f(*args, **kwargs)
else:
to = f(*args, **kwargs)
while True:
if type(to) is GeneratorType:
stack.append(to)
to = next(to)
else:
stack.pop()
if not stack:
break
to = stack[-1].send(to)
return to
return wrappedfunc
# 927 ms
def solve2():
n, = RI()
g = [[] for _ in range(n)]
for _ in range(n - 1):
u, v, w = RI()
u -= 1
v -= 1
g[u].append((v, w))
g[v].append((u, w))
d = RILST()
down1, down2, up = [0] * n, [0] * n, [0] * n
@bootstrap
def dfs(u, fa):
for v, w in g[u]:
if v == fa:
continue
yield dfs(v, u)
s = max(down1[v], d[v]) + w
if s > down1[u]:
down2[u] = down1[u]
down1[u] = s
elif s > down2[u]:
down2[u] = s
yield
@bootstrap
def reroot(u, fa):
for v, w in g[u]:
if v != fa:
if down1[u] == down1[v] + w or down1[u] == d[v] + w:
up[v] = max(down2[u] + w, up[u] + w, d[u] + w)
else:
up[v] = max(down1[u] + w, up[u] + w, d[u] + w)
yield reroot(v, u)
yield
dfs(0, -1)
reroot(0, -1)
print(*[max(a, b) for a, b in zip(up, down1)], sep='\n')
# 715 ms
def solve3():
n, = RI()
g = [[] for _ in range(n)]
for _ in range(n - 1):
u, v, w = RI()
u -= 1
v -= 1
g[u].append((v, w))
g[v].append((u, w))
d = RILST()
down1, down2, up = [0] * n, [0] * n, [0] * n
order = []
q = deque([0])
fas = [-1] * n
while q:
u = q.popleft()
order.append(u)
for v, w in g[u]:
if v != fas[u]:
fas[v] = u
q.append(v)
for u in order[::-1]:
for v, w in g[u]:
if v == fas[u]:
continue
s = max(down1[v], d[v]) + w
if s > down1[u]:
down2[u] = down1[u]
down1[u] = s
elif s > down2[u]:
down2[u] = s
for u in order:
for v, w in g[u]:
if v != fas[u]:
if down1[u] == down1[v] + w or down1[u] == d[v] + w:
up[v] = max(down2[u] + w, up[u] + w, d[u] + w)
else:
up[v] = max(down1[u] + w, up[u] + w, d[u] + w)
print(*[max(a, b) for a, b in zip(up, down1)], sep='\n')
if __name__ == '__main__':
solve()
5. 换根dp求去掉一个叶子的值。
链接: 2538. 最大价值和与最小价值和的差值
- 这题是周赛T4,我当时用树形DP写了一大堆两次dfs做出来了。
手写换根
class Solution:
def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:
g = [[] for _ in range(n)]
for u,v in edges:
g[u].append(v)
g[v].append(u)
# print(u,v)
ans = 0
f = [[0,0,0] for _ in range(n)] # f[i][0/1/2]代表:i向下走最大路径和,向下走次大路径和,向上走最大路径和;答案一定在向下或向上走的路径中
def dfs1(u,fa): # 更新向下走的最大/次大路径和
f[u][0] = p = price[u]
for v in g[u]:
if v != fa:
dfs1(v,u)
x = f[v][0]+p
if f[u][0]<x:
f[u][1] = f[u][0]
f[u][0] = x
elif f[u][1] < x:
f[u][1] = x
def dfs2(u,fa):
for v in g[u]:
if v != fa:
p = price[v]
if f[u][0] == f[v][0] + price[u]:
f[v][2] = max(f[u][2],f[u][1]) + p
else:
f[v][2] = max(f[u][2],f[u][0]) + p
dfs2(v,u)
dfs1(0,-1)
dfs2(0,-1)
return max(max(a-price[i],c-price[i]) for i,(a,_,c) in enumerate(f))
套模板
from typing import List, Tuple, Optional
from collections import defaultdict, Counter, deque
MOD = int(1e9 + 7)
INF = int(1e20)
# 给你一个 n 个节点的无向无根图,节点编号为 0 到 n - 1 。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。
# 每个节点都有一个价值。给你一个整数数组 price ,其中 price[i] 是第 i 个节点的价值。
# 一条路径的 价值和 是这条路径上所有节点的价值之和。
# 你可以选择树中任意一个节点作为根节点 root 。选择 root 为根的 开销 是以 root 为起点的所有路径中,价值和 最大的一条路径与最小的一条路径的差值。
# 请你返回所有节点作为根节点的选择中,最大 的 开销 为多少。
from typing import Callable, Generic, List, TypeVar
T = TypeVar("T")
E = Callable[[int], T]
"""identify element of op, and answer of leaf"""
Op = Callable[[T, T], T]
"""merge value of child node"""
Composition = Callable[[T, int, int, int], T]
"""return value from child node to parent node"""
class Rerooting(Generic[T]):
__slots__ = ("g", "_n", "_decrement", "_root", "_parent", "_order")
def __init__(self, n: int, decrement: int = 0, edges=None):
"""
n: 节点个数
decrement: 节点id可能需要偏移 (1-indexed则-1, 0-indexed则0)
"""
self.g = g = [[] for _ in range(n)]
self._n = n
self._decrement = decrement
self._root = None # 一开始的根
if edges:
for u, v in edges:
u -= decrement
v -= decrement
g[u].append(v)
g[v].append(u)
def add_edge(self, u: int, v: int):
"""
无向树加边
"""
u -= self._decrement
v -= self._decrement
self.g[u].append(v)
self.g[v].append(u)
def rerooting(
self, e: E["T"], op: Op["T"], composition: Composition["T"], root=0
) -> List["T"]:
"""
- e: 初始化每个节点的价值
(root) -> res
mergeの単位元
例:求最长路径 e=0
- op: 两个子树答案如何组合或取舍
(childRes1,childRes2) -> newRes
例:求最长路径 return max(childRes1,childRes2)
- composition: 知道子子树答案和节点值,如何更新子树答案
(from_res,fa,u,use_fa) -> new_res
use_fa: 0表示用u更新fa的dp1,1表示用fa更新u的dp2
例:最长路径return from_res+1
- root: 可能要设置初始根,默认是0
<概要> 换根DP,用线性时间获取以每个节点为根整颗树的情况。
注意最终返回的dp[u]代表以u为根时,u的所有子树的最优情况(不包括u节点本身),因此如果要整颗子树情况,还要再额外计算。
1. 记录dp1,dp2。其中:
dp1[u] 代表 以u为根的子树,它的孩子子树的最优值,即u节点本身不参与计算。注意,和我们一般定义的f[u]代表以u为根的子树2情况不同。
dp2[v] 代表 除了v以外,它的兄弟子树的最优值。依然注意,v不参与,同时u也不参与(u是v的父节点)。
建议画图理解。
2. dp2[v]的含义后边将进行一次变动,变更为v的兄弟、u的父过来的路径,merge上u节点本身最后得出来的值。即v以父亲为邻居向外延伸的最优值(不含v,但含父)。
3. 同时dp1[u]的含义更新为目标的含义:以u为根,u的子节点们所在子树的最优情况。
4. 这样dp1,dp2将分别代表u的向下子树的最优,u除了向下子树以外的最优(一定从父节点来,但父节点可能从兄弟来或祖宗来)
<步骤>
1. 先从任意root出发(一般是0),获取bfs层序。这里是为了方便dp,或者直接dfs树形DP其实也是可以的,但可能会爆栈。
2. 自底向上dp,用自身子树情况更新dp1,除自己外的兄弟子树情况更新dp2。
3. 自顶向下dp,变更dp2和dp1的含义。这时对于u来说存在三种子树(强烈建议画图观察):
① u本身的子树,它们的最优解已经存在于之前的dp1[u]。
② u的兄弟子树+fa,它们的最优解=composition(dp2[u],fa,u,use_fa=1)。
③ 连接到fa的最优子树+fa,最优解=composition(dp2[fa],fa,u,use_fa=1)。
注意这里的dp2含义已变更,由于我们是自顶向下计算,因此dp2[fa]已更新。
②和③可以写一起来更新dp2[u]
計算量 O(|V|) (Vは頂点数)
参照 https://qiita.com/keymoon/items/2a52f1b0fb7ef67fb89e
"""
# step1
root -= self._decrement
assert 0 <= root < self._n
self._root = root
g = self.g
_fas = self._parent = [-1] * self._n # 记录每个节点的父节点
_order = self._order = [root] # bfs记录遍历层序,便于后续dp
q = deque([root])
while q:
u = q.popleft()
for v in g[u]:
if v == _fas[u]:
continue
_fas[v] = u
_order.append(v)
q.append(v)
# step2
dp1 = [e(i) for i in range(self._n)] # !子树部分的dp值,假设u是当前子树的根,vs是第一层儿子(它的非父邻居),则dp1[u]=op(dp1(vs))
dp2 = [e(i) for i in
range(self._n)] # !非子树部分的dp值,假设u是当前子树的根,vs={v1,v2..vi..}是第一层儿子(它的非父邻居),则dp2[vi]=op(dp1(vs-vi)),即他的兄弟们
for u in _order[::-1]: # 从下往上拓扑序dp
res = e(u)
for v in g[u]:
if _fas[u] == v:
continue
dp2[v] = res
res = op(res, composition(dp1[v], u, v, 0)) # op从下往上更新dp1
# 由于最大可能在后边,因此还得倒序来一遍
res = e(u)
for v in g[u][::-1]:
if _fas[u] == v:
continue
dp2[v] = op(res, dp2[v])
res = op(res, composition(dp1[v], u, v, 0))
dp1[u] = res
# step3 自顶向下计算每个节点作为根时的dp1,dp2的含义变更为:dp2[u]为u的兄弟+父。这样对v来说dp1[u] = op(dp1[fa],dp1[u])
for u in _order[1:]: #
fa = _fas[u]
dp2[u] = composition(
op(dp2[u], dp2[fa]), fa, u, 1
) # op从上往下更新dp2
dp1[u] = op(dp1[u], dp2[u])
return dp1
class Solution:
def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:
def e(root: int) -> int:
# mergeの単位元
# 例:最も遠い点までの距離を求める場合 e=0
return 0
def op(child_res1: int, child_res2: int) -> int:
# 如何组合/取舍两个子树的答案
# 例:求最长路径 return max(childRes1,childRes2)
return max(child_res1, child_res2)
def composition(from_res: int, fa: int, u: int, use_fa: int = 0) -> int:
# 知道子树的每个子树和节点值,如何更新子树答案;
# 例子:求最长路径 return from_res+1
if use_fa == 0: # cur -> parent
return from_res + price[u]
return from_res + price[fa]
R = Rerooting(n, edges=edges)
# for u, v in edges:
# R.add_edge(u, v)
res = R.rerooting(e, max, composition)
return max(res)


![[QMT]04-在QMT之外调用xtquant直接编写策略](https://img-blog.csdnimg.cn/img_convert/3b4021d7cde26ee778b08d28013e9bb4.png)