前言

背包问题：给我们 i 件物品，每件物品都有体积 vi 和权重 wi ，给我们限制条件，让我们选择在背包的容量内，物品达到权重最大

01背包问题

01背包问题描述：每件物品只可以使用一次

我们看一下题目长什么样：

#include <iostream>

using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N][N];//f(i, j)表示体积j的情况下，前i件物品的最大价值

int main()
{
    int n, m;
    cin >> n >>m;
    
    for(int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            //第 i个物品先不选
            f[i][j] = f[i - 1][j];
            //第 i个物品选：首先要满足第 i个物品能放进来！能装第i个物品，需要决策是否装第i个物品
			if(j >= v[i]) f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }
    }
    
    cout << f[n][m] << endl;
    
    return 0;
}

到这里，我们上面实现的是二维状态方程，我们如何进行优化呢，题目中只要我们计算 f[n][m]，而其他的没有要求我们进行计算

注意：这里的 j 必须从大到小来枚举，若j从小到大，f[j-v[i]]中，由于j-v[i]小于j，f[j-v[i]]已经在i这层循环被计算了，而我们想要的f[j-v[i]]应该是i-1层循环里面的，所以j从大到小的话保证此时的f[j-v[i]]还未被计算，也就是第i-1层的数据

#include <iostream>

using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N];

int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);
    
    for(int i = 1; i <= n; i++)
        for(int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;
    
    return 0;
}

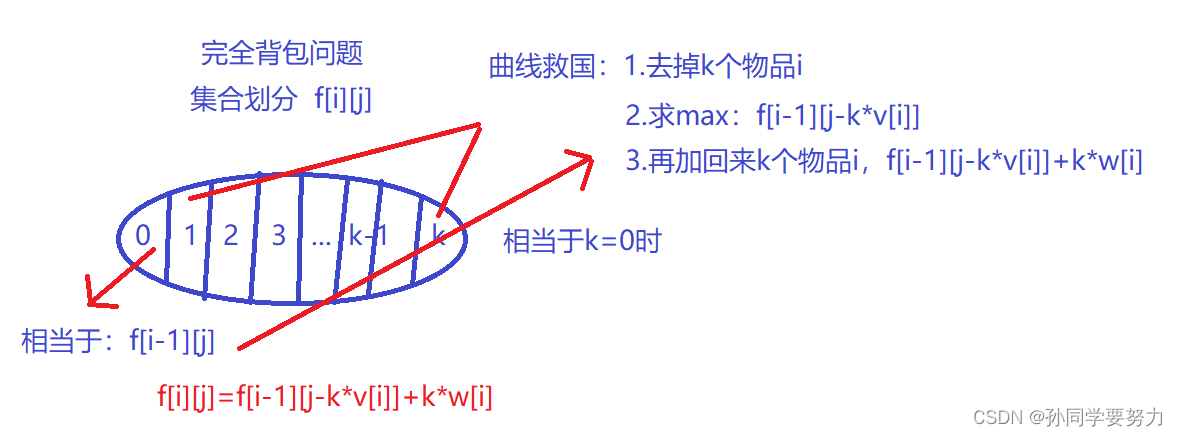
完全背包问题

完全背包问题：每个物品可以无限次使用

#include <iostream>

using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N][N];

int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
        {
            for(int k = 0; k * v[i] <= j; k++)
            {
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
            }
        }
        
    cout << f[n][m] << endl;
    
    return 0;
}

显然，上面有三层循环，效率很慢很慢，数据有可能过不了；我们来看看有什么可以优化的地方；

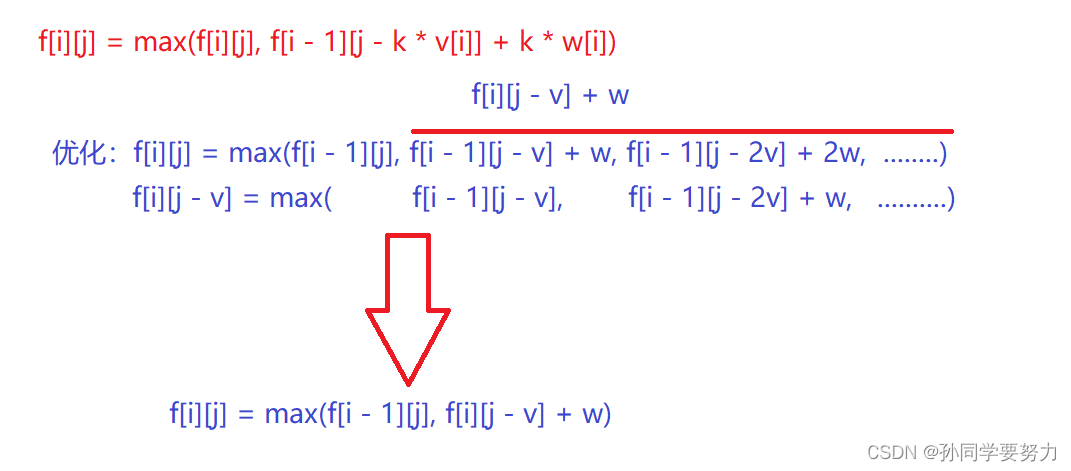
#include <iostream>

using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N][N];

int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            if(j - v[i] >= 0) f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
        }
        
    cout << f[n][m] << endl;
    
    return 0;
}

将上述代码更上一层口，使用一维状态方程

#include <iostream>

using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N];

int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);
    
    for(int i = 1; i <= n; i++)
        for(int j = v[i]; j <= m; j++)
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
        
    cout << f[m] << endl;
    
    return 0;
}

多重背包问题

多重背包问题会在完全背包问题上加一个限制，每个背包不是无限次使用，而是有个数限制

例题：

#include <iostream>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d%d%d", &v[i], &w[i], &s[i]);
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            for(int k = 0; k <= s[i] && k * v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                
    cout << f[n][m] << endl;
    
    return 0;
}

分组背包问题

分组背包问题：把所有物品分到各个组里面，每个组里面只可以选一件物品；

例题：

#include <iostream>

using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        cin >> s[i];
        for(int j = 1; j <= s[i]; j++)
        {
            cin >> v[i][j] >> w[i][j];
        }
    }
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];//不选第i个物品
            for(int k = 0; k <= s[i]; k++)
            {
                if(j >= v[i][k]) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);//选第i个物品
            }
        }
    }
    
    cout << f[n][m] << endl;
    
    return 0;
}

我们将它优化成一维状态方程：

#include <iostream>

using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        cin >> s[i];
        for(int j = 1; j <= s[i]; j++)
        {
            cin >> v[i][j] >> w[i][j];
        }
    }
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = m; j >= 1; j--)
        {
            for(int k = 0; k <= s[i]; k++)
            {
                if(j >= v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
            }
        }
    }
    
    cout << f[m] << endl;
    
    return 0;
}