字典学习简介

如果把降维理解成压缩的话，那么字典学习的本质是编码，其目的是找到少量的原子，用以描述或构建原始样本。举个一维的例子，以abcabcabc为例，很显然abc就是一个院子，这个字符串无非是abc重复了三次而已，用abc这个词条，或者说原子，就可以构建abcabcabc这样的字符串。

一般来说，字典学习所面对的并不是一个字符串，而是一个稀疏矩阵，基于此，需要对一些概念做下定义

• 原始样本$Y$，就是原始矩阵
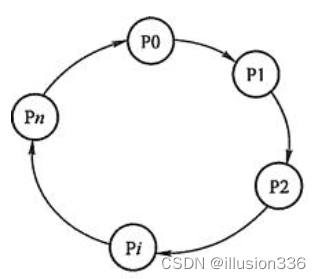
• 字典矩阵$D$，内部含有的词条为列向量，被称为原子，记作$d_k$
• 稀疏矩阵$X$，可以理解为查字典的方法

从而，$Y=DX$就是通过$X$来查阅$D$从而得到$Y$的过程，在sklearn中，字典学习实际上是求解如下优化问题

$$\begin{gathered} (D,X)=\mathrm{argmin}0.5\Vert Y-DX{\Vert }_F^2+\alpha \Vert X{\Vert }_{1,1} \\ D,Xwith\Vert X_k{\Vert }_2⩽1\forall 0⩽k<N \end{gathered}$$

其中$\Vert {\Vert }_{1,1}$表示对矩阵中所有实数求和；$\Vert {\Vert }_F$为佛罗贝尼乌斯范数，可定义为

$$\Vert A{\Vert }_F=\sqrt{\sum _{i=1}^n\sum _{j=1}^n|a_{ij}{|}^2}=\sqrt{\mathrm{trace}(AA)}$$

构造函数

字典学习作为类被封装在sklearn中，其构造函数如下

class decomposition.DictionaryLearning(n_components=None, *, alpha=1, max_iter=1000, tol=1e-08, fit_algorithm='lars', transform_algorithm='omp', transform_n_nonzero_coefs=None, transform_alpha=None, n_jobs=None, code_init=None, dict_init=None, verbose=False, split_sign=False, random_state=None, positive_code=False, positive_dict=False, transform_max_iter=1000)

其中，n_components为要提取的元素个数，alpha即为前文公式中的$\alpha$，表示稀疏控制参数。

由于构造函数参数太多，故只则取一些常用参数

fit_algorithm 为拟合算法，可选

• 'lars'： 最小角回归
• 'cd'：坐标下降

transform_algorithm 为数据转换方案：

• 'lars'：最小角回归
• 'lasso_lars'：lasso最小角回归
• 'lasso_cd'：lasso坐标下降
• 'omp': 正交匹配追踪
• 'threshold': 阈值法，将字典所有小于$\alpha$的值置为0

当transform_algorithm为lars或omp时，可选参数transform_n_nonzero_coefsint，表示$D$的每一列中非零系数的目标值。

此外，还有一些通用的参数：max_iter表示最大迭代次数；tol 表示最大误差；n_jobs表示并行进程数；random_state为随机数状态，便于成果复现。

考虑到在处理矩阵问题时往往比较耗时，所以提供了小批字典学习类MiniBatchDictionaryLearning，便于处理较大数据，其构造函数与字典学习基本相同。

实战

Step1 制作实验数据

sklearn官网提供了基于字典学习进行图像去噪的例子，首先向图像中添加噪声，得到类似下图这样的

代码为

import matplotlib.pyplot as plt
import numpy as np

img = plt.imread("lean_gray.jpg")/255.0
h, w = img.shape
imNoise = img*1
mid = w//2
imNoise[:, mid:] += 0.1 * np.random.randn(h, mid)

def showError(imNoise, img, title):
    plt.subplot(1, 2, 1)
    plt.imshow(imNoise, vmin=0, vmax=1, cmap=plt.cm.gray)
    plt.title("image")
    plt.axis('off')
    plt.subplot(1, 2, 2)
    err = imNoise - img
    msg = f"err std:{np.std(err):.2f}"
    plt.title(msg) 
    plt.imshow(err, vmin=-0.5, vmax=0.5, cmap=plt.cm.PuOr)
    plt.axis('off')
    plt.suptitle(title)

showError(imNoise, img, "Distorted image")
plt.show()

Step2 小批字典学习

接下来，创建MiniBatchDictionaryLearning对象，并fit，完成训练，然后查看一下字典学习中的"原子"components_

from sklearn.decomposition import MiniBatchDictionaryLearning as mbdl

from sklearn.feature_extraction.image import extract_patches_2d as ep2d

patch_size = (7, 7)
data = extract_patches_2d(imNoise[:, : mid], patch_size)
data = data.reshape(data.shape[0], -1)
# 按行归一化
data = (data-np.mean(data, axis=0))/ np.std(data, axis=0)

### ！！！！！！！！！！！！！！！！！！！！
dico = mbdl(n_components=50, batch_size=200,alpha=1.0, max_iter=10)
dico.fit(data)
X = dico.components_
### ！！！！！！！！！！！！！！！！！！！！

for i, comp in enumerate(X[:50]):
    plt.subplot(5, 10, i + 1)
    plt.imshow(comp.reshape(patch_size))
    plt.axis('off')

Step 3 参数调整

最后，调整参数，对比不同情况下字典学习的效果，如图所示

A	B

代码如下

from sklearn.feature_extraction.image import reconstruct_from_patches_2d

data = extract_patches_2d(imNoise[:, mid:], patch_size)
data = data.reshape(data.shape[0], -1)
intercept = np.mean(data, axis=0)
data -= intercept

tf_algs = [
    ("omp @1 atom", "omp", 
        {"transform_n_nonzero_coefs": 1}),
    ("omp @2 atoms", "omp", 
        {"transform_n_nonzero_coefs": 2}),
    ("las @4 atoms", "lars", 
        {"transform_n_nonzero_coefs": 4}),
    ("Thresholding @ alpha=0.1", "threshold",
        {"transform_alpha": 0.1}),
]

recons = {}
for title, tf_alg, kwargs in tf_algs:
    print(title + "...")
    recons[title] = img.copy()
    dico.set_params(transform_algorithm=tf_alg, **kwargs)
    code = dico.transform(data)
    Ys = np.dot(code, X)
    Ys += intercept
    Ys = Ys.reshape(len(data), *patch_size)
    if tf_alg == "threshold":
        Ys = (Ys - Ys.min())/Ys.max()
    recons[title][:, mid:] = reconstruct_from_patches_2d(
        Ys, (h, mid))
    plt.figure(title)
    showError(recons[title], img, title)

plt.show()