连载文章,长期更新,欢迎关注:
在7.2.4节中,讨论了表示机器人观测与运动之间依赖关系的概率图模型,主要是贝叶斯网络(实际应用在机器人中的是动态贝叶斯网络)和马尔可夫网络(实际应用在机器人中的是因子图)。在概率图模型表示的基础上,就可以利用可观测量(和
)推理不可观测量(
和
),这个概率推理过程也叫状态估计,在7.3节中对基础性的估计理论已经进行了讨论。前面这些关于表示和推理的讨论都是基于一般情况而言,不涉及机器人实际量测数据。本节就来引入机器人实际量测数据,并基于贝叶斯网络表示这些数据的关系,基于这种表示,状态估计很容易进行,一般采用贝叶斯估计。
贝叶斯估计是一种通用框架,具体形式包括最小均方误差估计、最大后验估计等,其核心是在后验概率分布中,最小化误差的期望,这些已经在7.3.2节有讨论。那么,下面就来讨论引入机器人实际量测数据时,后验概率分布的具体形式。假设量测数据由图7-19所示的动态贝叶斯网络表示,可以从图中看出,根据选取估计量的不同,又分为几种估计问题。如果仅对机器人当前位姿状态进行状态估计,这就是定位问题,对应的后验概率分布表述如式(7-88)所示。如果除了估计机器人当前位姿状态
,还对地图
同时进行估计,这就是在线SLAM问题,对应的后验概率分布表述如式(7-89)所示。如果要对机器人所有历史位姿状态
和地图
同时进行估计,这就是完全SLAM问题,对应的后验概率分布表述如式(7-90)所示。

由于(7-88)所示的定位问题和(7-89)所示的在线SLAM问题求解过程都是类似的,也就是所谓的滤波方法。为了使讨论过程更加简洁,就拿式(7-88)来展开分析,由于式(7-88)中的地图条件是常量可以忽略,那么讨论形式就可以进一步简化为
。本节内容旨在通过对
的分析,让大家掌握滤波方法的基础原理。而基于滤波方法基础原理的典型在线SLAM系统实现框架EKF-SLAM将在7.7.1节中详细讨论,基于滤波方法基础原理的典型完全SLAM系统实现框架Fast-SLAM将在7.7.2节中详细讨论。
虽然式(7-90)所示的完全SLAM系统可以用滤波方法求解,比如著名的Fast-SLAM实现框架。但是,贝叶斯网络表示下的完全SLAM系统能很方便地转换成因子图表示,这部分内容已经在7.2.4节中讨论过了。利用因子图表示完全SLAM问题,然后用最小二乘估计进行求解会更方便,这部分内容将在7.5节中展开。
7.4.1 贝叶斯估计
为了后面讨论方便,将后验概率分布用符号
替代,
常常也称为置信度。下面结合机器人量测数据
和
,分析
的具体形式[4] p31~33。首先利用式(7-29)所示的贝叶斯准则将
进行分解,分解结果如式(7-91)所示。式中的分母
由量测数据可以直接计算,是一个常数值,因此可以忽略。为了保证
是一个求和为1的概率分布,需要乘以归一化常数
保证其合法性。剩下就是
和
两项概率分布的乘积。

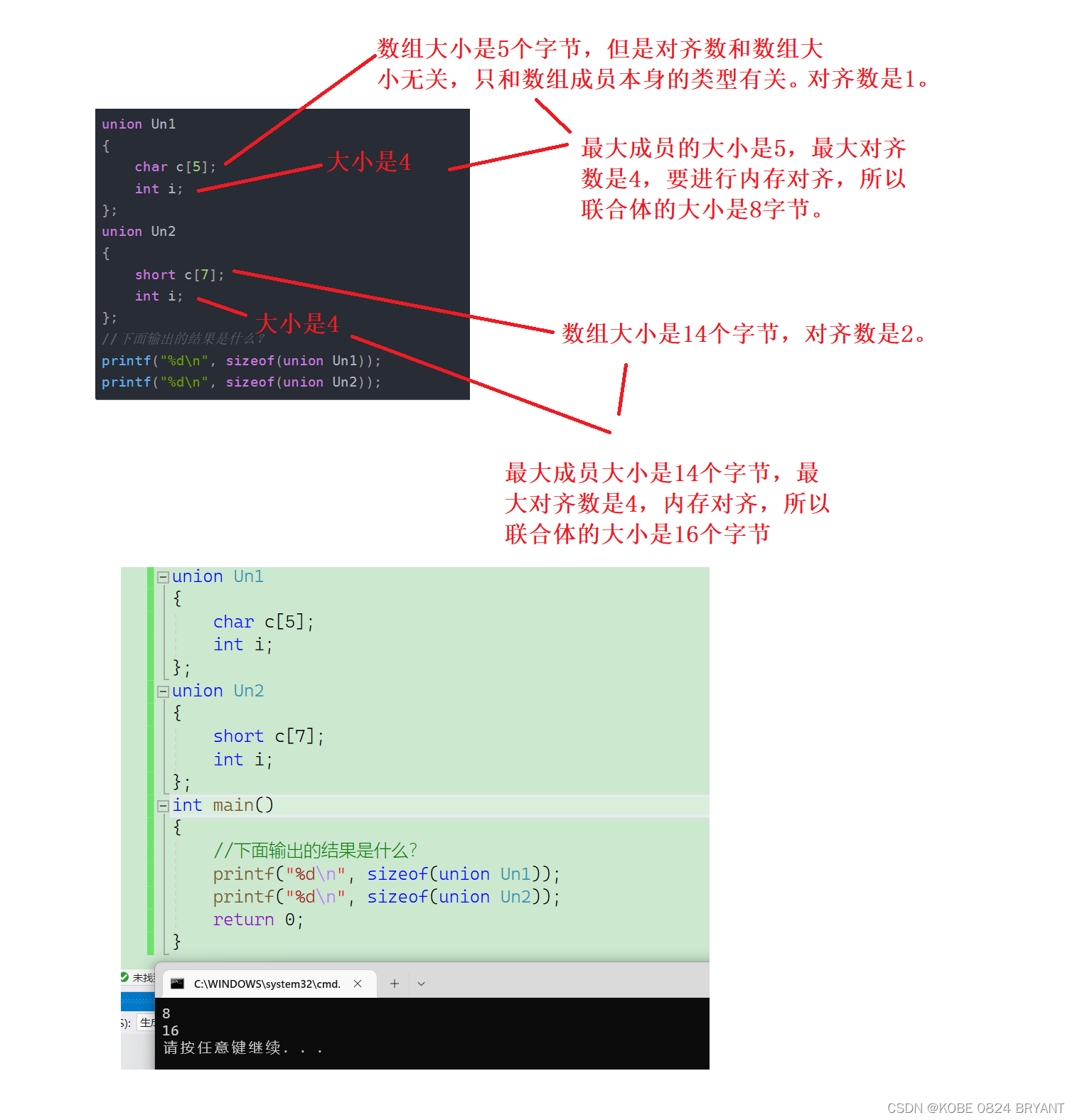
在贝叶斯网络中,有一条很重要的性质就是条件独立性。例如,除了直接指向某节点的原因节点外,其他所有节点与该节点都是条件独立的。利用这个条件独立性,可以进行式(7-92)所示的化简。
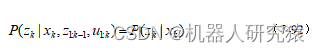
另外,可利用全概率公式进行式(7-93)所示的化简。
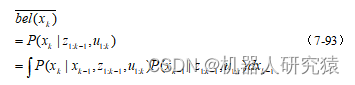
同样,利用条件独立性,可以进行式(7-94)所示的化简。
![]()
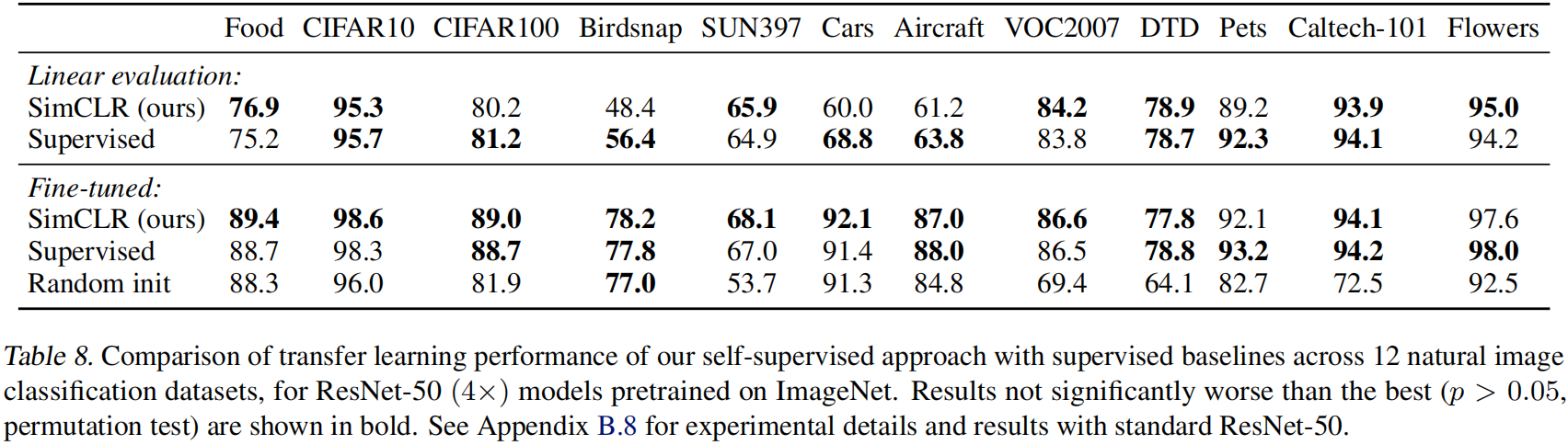
而根据常识,时刻的控制量
并不会影响
时刻的状态
,所以可以进行式(7-95)所示的化简。
![]()
将式(7-94)和(7-95)代入(7-93),化简结果如式(7-96)所示。
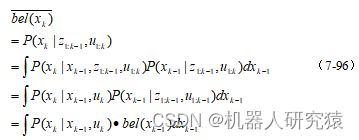
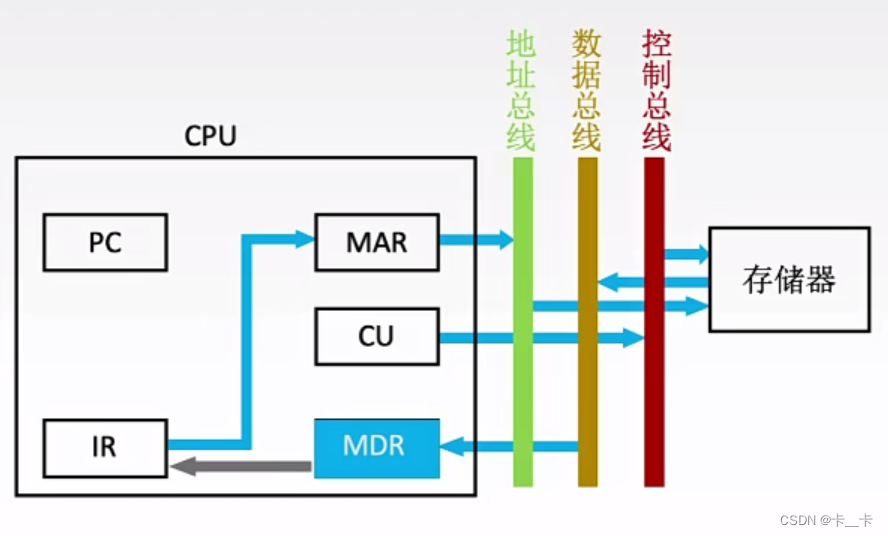
再将式(7-96)和(7-92)代入(7-91),化简结果就是后验概率分布的最终结果了,如式(7-97)所示。
![]()
那么,后验概率分布的计算过程可以整理成下式(7-98)所示的形式。其中
为运动模型的概率分布,
为观测模型的概率分布,计算方法见7.2.2节和7.2.3节,也就是说
和
由机器人量测数据给出。在已知状态初始值
的置信度后,利用运动数据
和前一时刻置信度
预测出当前状态置信度
,这个过程称为运动预测。由于运动预测存在较大误差,所以还需要利用观测数据
对预测
进行修正,修正后的置信度为
,这个过程称为观测更新。
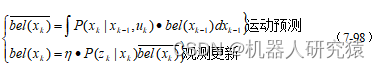
很显然,式(7-98)所示计算后验概率分布的算法是一个递归过程,因此这个算法也称为递归贝叶斯滤波。
由于后验概率分布没有给定确切的形式,也就是说递归贝叶斯滤波是一种通用框架。在给定不同形式的
分布后,递归贝叶斯滤波也就对应不同形式的算法实现。应用最广泛的分布当属高斯分布了,高斯分布能表示复杂噪声的随机性,并且易于进行数学处理,并且满足递归贝叶斯滤波中先验与后验之间共轭特性。按照高斯分布、非高斯分布、线性系统和非线性系统,递归贝叶斯滤波可以划分出如表7-2所示的4种情况。
表7-2 4种情况
| 高斯分布 | 非高斯分布 | |
| 线性系统 | 线性高斯系统 KF、IF | 线性非高斯系统 |
| 非线性系统 | 非线性高斯系统 EKF、UKF、EIF | 非线性非高斯系统 HF、PF |
下面的讨论,首先从最简单的线性高斯系统入手,基于矩参数表示高斯分布,引出卡尔曼滤波(KF)。然后讨论更为复杂的非线性高斯系统,引出扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)。当然也可以基于正则参数表示高斯分布,线性高斯系统中对应就是信息滤波(IF)。非线性高斯系统,对应就是扩展信息滤波(EIF)。然而,实际问题往往是非线性非高斯系统这样更一般的情况。如果用概率密度函数来完整表示
的非高斯分布情况,
将是一个无限维空间中的函数,显然不现实。另外,高维概率密度函数
在非线性系统中运算复杂度非常高,计算代价将难以承受。因此,在非线性非高斯系统中必须进行近似计算以提高效率,虽然近似会带来精度的损失。在非线性非高斯系统中,利用非参数方式表示概率分布,典型实现算法就是直方图滤波(HF)和粒子滤波(PF)。
当然,式(7-98)所示的递归贝叶斯滤波框架,只是给出了后验概率分布的计算方法。而状态估计是后验概率分布
和估计策略结合的产物。也就是说在讨论递归贝叶斯滤波的具体实现时,还需要讨论估计策略,以保证估计效果足够好。
7.4.2 参数化实现
高斯分布可以用矩参数(均值和方差)进行表示,机器人中涉及的都是多维变量,所以这里讨论多维高斯分布,如式(7-99)所示。其中是
维向量,均值
是
维向量, 协方差矩阵协方差矩阵
是
的对称阵。式中
,表示求矩阵
行列式的运算。
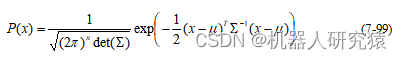
高斯分布也可以用正则参数表示,即信息矩阵和信息向量
。矩参数(
和
)与正则参数(
和
)存在式(7-100)所示的关系。

其实,通过将式(7-99)进行展开,然后将式(7-100)代入展开式中,很容易得到高斯分布的正则参数表示形式,如式(7-101)所示。式中的为归一化常数项。

可以发现,用矩参数表示高斯分布,物理意义更加直观;而用正则参数表示高斯分布,表示形式更加简洁。
1.卡尔曼滤波
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
2.信息滤波
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
7.4.3 非参数化实现
虽然已经用矩参数和正则参数表示高斯分布,得到了处理线性高斯系统的线性卡尔曼滤波和线性信息滤波,和处理非线性高斯系统的扩展卡尔曼滤波、无迹卡尔曼滤波和扩展信息滤波。然而,实际问题往往是非线性非高斯系统这样更一般的情况。如果用概率密度函数来完整表示
的非高斯分布情况,
将是一个无限维空间中的函数,显然不现实。另外,高维概率密度函数
在非线性系统中运算复杂度非常高,计算代价将难以承受。因此,在非线性非高斯系统中必须进行近似计算以提高效率,虽然近似会带来精度的损失。在非线性非高斯系统中,利用非参数方式表示概率分布,典型实现算法就是直方图滤波和粒子滤波。
在卡尔曼滤波和信息滤波中,需要用矩参数或正则参数对高斯分布进行参数化表示,然后对这些参数进行闭式递归计算。然而,当分布不是高斯分布这种特殊形式时,就需要用一个无限维概率密度函数描述,这这种参数化显然不现实。这里介绍两种非参数化方法来表示这种非高斯分布,即直方图和粒子。
1.直方图滤波
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
2.粒子滤波
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
参考文献
【1】 张虎,机器人SLAM导航核心技术与实战[M]. 机械工业出版社,2022.





![[LeetCode周赛复盘] 第 329 场周赛20230122](https://img-blog.csdnimg.cn/b66cc45759404ae0976081c19c9c3e77.png)