连载文章，长期更新，欢迎关注：

针对式（7-38）所述的在线SLAM系统，以扩展卡尔曼滤波（EKF）为代表的滤波方法，是求解该状态估计问题最典型的方法，在7.4节中已经详细讨论了这些滤波方法的基础原理，而基于滤波方法基础原理的两种典型实现框架EKF-SLAM和Fast-SLAM将在下面进行详细讨论。虽然式（7-39）所示的完全SLAM系统可以用滤波方法求解，比如著名的Fast-SLAM实现框架。但是，贝叶斯网络表示下的完全SLAM系统能很方面地转换成因子图表示，这部分内容已经在7.2.4节中讨论过了。利用因子图表示完全SLAM问题，然后用最小二乘估计进行求解会更方便。

针对式（7-39）所述的完全SLAM系统，优化方法是求解该状态估计问题最典型的方法。这部分内容，首先将贝叶斯网络表示的SLAM问题转化到因子图表示。这样贝叶斯网络中的最大后验估计就等效为因子图中的最小二乘估计，这种最小二乘估计常常是非线性最小二乘估计。在7.5节中已经介绍了这种非线性最小二乘估计的求解方法，一种方法是经过线性化近似后直接求解，这种直接求解方法的典型实现框架Graph-SLAM将在下面进行详细讨论；另一种方法是采用迭代方式间接求解，也就是所谓的优化方法，现今主流SLAM算法中大多数都基于这种优化方法。

按照在线SLAM还是完全SLAM，贝叶斯网络表示还是最小二乘表示，SLAM框架可以用表7-4来分类。

表7-4 SLAM框架分类

		在线SLAM系统	完全SLAM系统
贝叶斯网络表示	EKF滤波	EKF-SLAM
贝叶斯网络表示	粒子滤波		Fast-SLAM
最小二乘表示	直接法		Graph-SLAM
最小二乘表示	优化法		现今主流SLAM

7.7.1 EKF-SLAM

在7.4节中介绍滤波法的基本原理时，为了方便讨论，只考虑了估计机器人位姿状态 $x_{k}$ 这个最简单的情况，如式（7-88）所示。现在来讨论在线SLAM系统中同时估计机器人位姿状态 $x_{k}$ 和路标 $m=\left \{ m_{1},m_{2},...,m_{L} \right \}$ 的情况，如式（7-89）所示。求解在线SLAM问题，使用最早也最经典的方法就是基于EKF滤波方法，相应的实现框架就是EKF-SLAM[3] p306~318。

使用EKF滤波方法求解式（7-89）所示的在线SLAM问题，首先就是将估计问题的后验概率用高斯分布参数化表示，如式（7-169）所示。

其实，就是将待估计量 $x_{k}$ 和 $m=\left \{ m_{1},m_{2},...,m_{L} \right \}$ 用一个新的状态向量 $s_{k}$ 来集中表示。考虑新的状态估计量 $s_{k}$ ，那么机器人的运动和观测方程可以改写成式（7-170）和（7-171）所示形式。

其中 $r_{k}$ 为运动过程携带的高斯噪声，协方差矩阵记为 $R_{k}=\begin{bmatrix} {R_{k}}' & 0\\ 0 & 0 \end{bmatrix}$ ； $q_{k}$ 为观测过程携带的高斯噪声，协方差矩阵记为 $Q_{k}$ 。

这些变量定义好后，就可以直接拿式（7-116）所示EKF的5个核心公式进行滤波了。下面把这5个核心公式搬出来，如式（7-172），便于大家阅读。这就是EKF-SLAM框架的滤波实现过程，滤波器的输入是当前运动与观测量（ $u_{k}$ 和 $z_{k}$ ）和前一时刻的状态分布（ $\mu _{k-1}$ 和 $\Sigma _{k-1}$ ），滤波器的输出是当前时刻的状态分布（ $\mu _{k}$ 和 $\Sigma _{k}$ ）。可以看到滤波方法是一种增量求解方法，只需要输入新量测信息 $u_{k}$ 和 $z_{k}$ 就能完成对SLAM状态量的求解，也就是所谓的在线SLAM系统。

7.7.2 Fast-SLAM

以EKF-SLAM为代表的在线SLAM系统，其EKF滤波方法是一种增量求解方法，只需要输入新量测信息 $u_{k}$ 和 $z_{k}$ 就能完成对SLAM状态量的求解，这种增量求解方法具有很大优势。但是EKF-SLAM也有两个明显的缺点，一方面，其将所估计后验分布假设成高斯分布，非线性高斯系统必须被线性化近似成线性高斯系统，这种简单粗暴的线性化近似容易引起较大误差；另一方面，状态量 $s_{k}$ 的协方差矩阵 $\Sigma _{k}$ 的复杂度随路标数量是二次方增长，即 $O(L^{2})$ 复杂度，也就是说其无法建立大规模地图。为了解决线性化和构建大规模地图的问题，大家开始放弃EKF-SLAM这种在线SLAM增量求解的好处，转向完全SLAM系统的研究，如式（7-173）所示。

完全SLAM系统的一个方向仍然是基于贝叶斯的滤波方法，将EKF参数滤波换成非参数化的粒子滤波，这样就不用处理EKF中的非线性高斯系统线性化近似的问题了，并且还可以处理非线性非高斯系统这种更一般的情况。但是，如果每个状态用 $c$ 个粒子点表示其后验分布情况，那么表示所有状态的后验分布所需要的粒子点复杂度就是 $O(c^{k+L})$ 。其中RBPF（Rao-Blackwellization Particle Filter）这种改进版的粒子滤波，能将粒子点复杂度降低到 $O(c^{k})$ 。RBPF的思路是将SLAM问题中的机器人轨迹估计和路标估计分离开来，如式（7-174）所示，轨迹估计其实就是定位问题，采用粒子滤波来实现；在每个粒子点确定的一条机器人轨迹上，都可以用EKF来估计对应的路标，其实就是建图问题，采用EKF来实现。基于RPBF有很多具体的SLAM实现框架，Fast-SLAM就属于其中一种实现[3] p318~333。

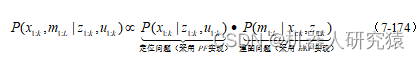
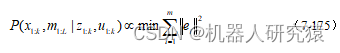
完全SLAM系统的另一个方向是基于最小二乘的方法，贝叶斯网络表示转化到了图结构表示，利用图结构中的约束关系构建非线性最小二乘，如式（7-175）所示，最后利用直接法或者迭代优化法求解该最小二乘。最小二乘法解决了EKF-SLAM中不能建立大规模地图的问题，因为最小二乘法只是将系统收集到的所有时刻信息构建成一个方程，求解该方程或者迭代求解，利用方程的稀疏性等特点很好求解，求解复杂度受建图规模的影响没那么大。

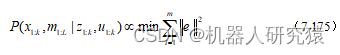
7.7.3 Graph-SLAM

现在讨论基于最小二乘的完全SLAM系统，其直接求解方法的典型实现框架是Graph-SLAM。从滤波法的最大后验推导出最小二乘表示，如式（7-50）所示。然后利用一阶泰勒展开将式（7-50）中的运动和观测函数线性化，就得到了式（7-126）所示的形式。在7.5.2节中已经介绍了求解式（7-126）所示线性方程的方法，就是采用Cholesky分解和QR分解对线性方程中的信息矩阵进行数值分解，间接性解线性方程。在Graph-SLAM中，解法也是类似的，只不过换了种说法，即所谓的信息滤波。

在Graph-SLAM中的信息滤波中，首先将式（7-126）所示线性方程替换成信息参数 $\Omega$ 和 $\xi$ 表示，关于信息参数与矩参数的关系，如式（7-100）所示。然后，该最小二乘的求解方式就转换成信息滤波过程了。可以看到Graph-SLAM中求解最小二乘的过程，是一种解析过程，即信息参数的预测和更新，也就是所谓的直接法。关于Graph-SLAM中信息滤波的具体过程，可以参考文献[4] p353~362中的内容，不要求大家掌握。

7.7.4 现今主流SLAM算法

虽然EKF-SLAM、Fast-SLAM和Graph-SLAM是最经典的几个SLAM框架，也囊括了SLAM的几个主要研究方向，但是只在学术上还会被提起，工程应用上已经不会使用这些框架了。工程应用中，现今主流SLAM算法大多是基于最小二乘的迭代优化求解，也就是所谓的优化方法。下面就介绍一些工程中常用的SLAM框架，如图7-39所示，当然其中也有一些不是优化方法的算法，只是列出来方便对比学习。