503. 下一个更大元素 II

注意点：

1. 初始化了2倍的题目中的nums.size()，最后直接/2即可

2. 分清逻辑nums[i] > nums[st.top()]的时候，才进行st.pop()操作

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        vector<int> nums1(nums.begin(), nums.end());//提高运算速度
        nums.insert(nums.end(), nums1.begin(), nums1.end());
        // 初始化了2倍的题目中的nums.size()，最后直接/2即可
        vector<int> result(nums.size(), -1);
        stack<int> st;
        st.push(0);
        
        for(int i = 1; i< nums.size(); i++) {
            if(nums[i] <= nums[st.top()]) st.push(i);
            else {
                while(!st.empty() && nums[i] > nums[st.top()]) {
                    result[st.top()] = nums[i];
                    st.pop();
                }
                st.push(i);
            }
        }
        result.resize(result.size()/2);
        return result;
    }
};

42. 接雨水 -- 三种方法：1.双指针 2.动态规划 3.单调栈

注意点：

1.采用双指针的方法，主要的策略是获得i列左右两侧最高的if(height[l] > lHeight) lHeight = height[l];，然后对左右两侧最高值取最小值min(rHeight, lHeight)，并与height[i]取差进行运算，最后所有的相加得到result，但是这种方法操作超时

class Solution {
public:
    int trap(vector<int>& height) {
        int result = 0;
        for(int i =0; i< height.size(); i++) {
            if(i == 0 || i == height.size()-1) continue;

            int rHeight = height[i];
            int lHeight = height[i];

            for(int r = i+1; r<height.size(); r++) {
                if(height[r] > rHeight) rHeight = height[r];
            }
            for(int l = i-1; l>=0; l--) {
                if(height[l] > lHeight) lHeight = height[l];
            }

            int h = min(rHeight, lHeight)-height[i];
            if(h>0)result +=h;
        }
        return result;
    }
};

2.采用动态规划方法

注意点：

1. 对height[i]的左侧求最大值的递推公式是： maxLeft[i] = max(height[i], maxLeft[i-1]);同理对height[i]的右侧求最大值的递推公式是： maxRight[i] = max(height[i], maxRight[i+1]);

2. 根据递推公式可以推出maxLeft[i]是从右到左进行遍历的，maxRight[i]是从右到左进行遍历的，所以进行了初始化

3. 最后因为没有对height[0]和height[height.size()-1]进行排除，所以需要if判断一下如果是正数再进行加法

class Solution {
public:
    int trap(vector<int>& height) {
        
        vector<int> maxLeft(height.size(),0);
        vector<int> maxRight(height.size(),0);

        maxLeft[0] = height[0];
        // 根据递推公式得到左序遍历
        for(int i = 1; i<height.size(); i++) {
            // 递推公式，求对一个数左侧的最大值
            maxLeft[i] = max(height[i], maxLeft[i-1]);
        }


        maxRight[height.size()-1] = height[height.size()-1];
        // 根据递推公式得到右序遍历
        for(int i = height.size()-2; i>=1; i--) {
            // 求一个数右侧的最大值
            maxRight[i] = max(height[i], maxRight[i+1]);
        }

        
        int result = 0;
        for(int i = 0; i< height.size(); i++) {
            int h = min(maxLeft[i], maxRight[i])-height[i];
            // 因为没有对height[0]和height[height.size()-1]进行排除，所以需要if判断一下
            if (h >0)result +=h;
        }

        return result;

    }
};

单调栈

注意点：

1.这道题的思路：如果当前遍历的元素（柱子）高度大于栈顶元素的高度，此时就出现凹槽了

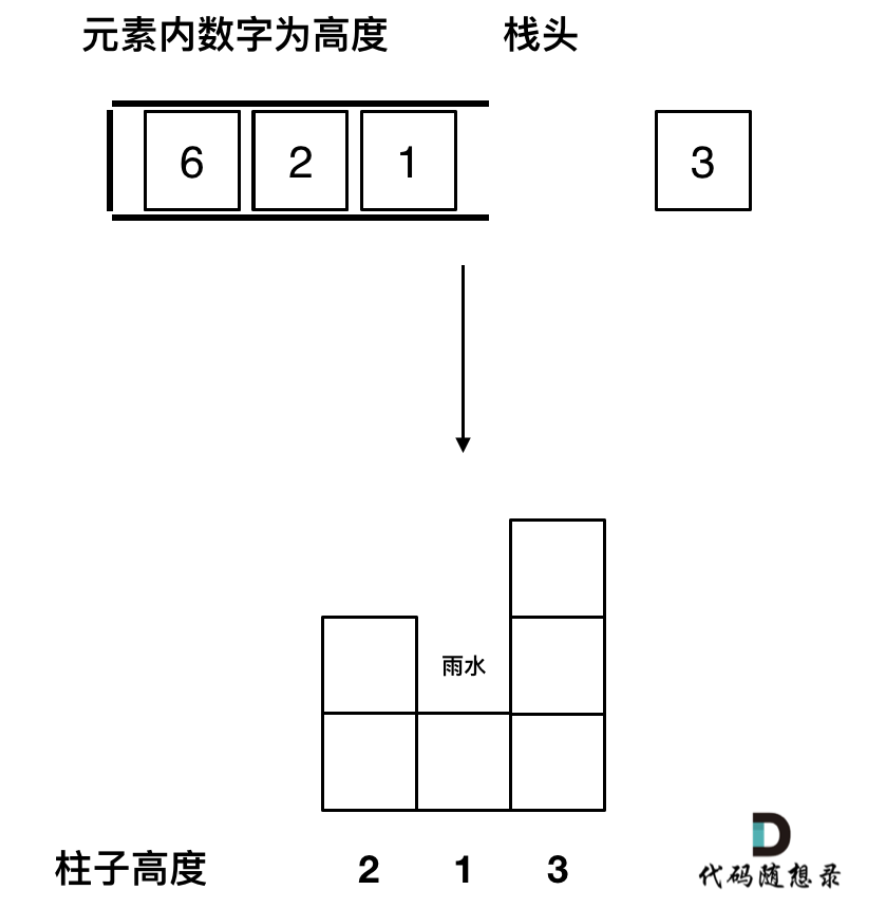
2.单调栈是顺序栈：栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序

3.当height[i] == height[st.top()]的时候将上一个弹出，以便最后计算横向数据的时候出现误差

class Solution {
public:
    int trap(vector<int>& height) {
        int result = 0;
        stack<int> st;
        st.push(0);
        for(int i = 1; i<height.size(); i++) {
            if(height[i] < height[st.top()]) {
                // 符合顺序遍历的顺序所以没有动
                st.push(i);
            } else if(height[i] == height[st.top()]) {
                // 当相等的时候需要将上一个弹出，以便计算w的时候没有误差
                st.pop();
                st.push(i);
            }else {
                while(!st.empty() && height[i] > height[st.top()]) {
                    int head = st.top();
                    // 将栈头扔掉
                    st.pop();
                    // if主要判断的是第0个元素
                    if(!st.empty()) {
                        // 计算纵向长度
                        int h = min(height[i], height[st.top()])-height[head];
                        // 计算横向长度
                        int w = i-st.top()-1;
                        // 最后计算面积
                        result += h*w;
                    }

                }
                st.push(i);
            }
        }
        return result;

    }
};