专栏：python
个人主页：HaiFan.
专栏简介：本专栏主要更新一些python的基础知识，也会实现一些小游戏和通讯录，学时管理系统之类的，有兴趣的朋友可以关注一下。

前言

---

元组和列表的大部分功能都是差不多的，但是有一个功能是有非常明显的区别：列表可变，创建好了，随时可以更改，
元组不可变，创建好了，改变不了，想要改变，只能丢弃旧的，创建个新的。

---

列表的的概念

在编程中，我们经常要使用变量，来保存数据或者表示数据。
如果代码中需要表示的数据个数比较少，我们直接创建多个变量即可。

a1 = 1
a2 = 2
a3 = 3

那么，要是想表示一到100，我们要创建100个变量吗？这样也能创建，如果要创建n个数据呢？这个时候，就没有办法用创建变量的方式，来表示数据了，在这里引出新的概念–列表/元组。

---

列表是一种让程序猿在代码中批量表示/保存数据的方式。

列表的创建

创建列表主要有两种方式，一种是[]表示一个空列表，还有一种是通过list()来创建列表

a = []
b = list()

print(type(a))
print(type(b))

---

如果需要往里面设置初始值，可以直接写在[]里面

a = [1,2,3,4]
print(a)

python中的列表，可以从放不同类型的元素，别问为啥，问就是python强大，这一点和其他语言差别较大。

a = [1,2,3,4,'hello world','haohaoxuexi']
print(a)

访问下标

可以通过下标访问操作符[]来获取列表中的任意元素
此[]非创建列表中的[]，如-1和1-2，-1的的-是负号的意思，1-2的-是减号的意思。
我们把 [ ] 中填写的数字, 称为 下标 或者 索引 .

a = [1,2,3,4]
print(a[1])

这个结果是1吗？

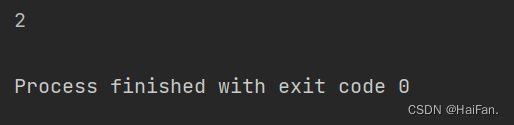
结果为什么会是2呢？这是因为，python中访问下标的时候，是从0开始的，0代表列表中第一个元素的位置，1代表列表中第二个元素的位置。所以上面代码的结果会是2。

---

通过下标还能改变列表中元素的值。

a = [1,2,3,4]
a[1] = 10000
print(a[1])

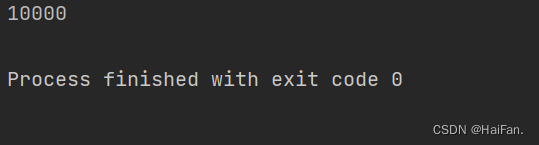
但是，访问下标的时候，下标不要超出列表的有效范围，否则会抛出异常。

a = [1,2,3,4]
a[1] = 10000
print(a[10000])

---

使用len函数，可以获取到列表的元素个数

a = [1,2,3,4]

print(len(a))

---

python中的下标可以取负数，表示倒数第几个元素

a = [1,2,3,4]

print(a[-1])

其实a[-1]等价于a[len(a) - 1]所以访问元素是倒着数的。

切片操作

通过下标操作是依次取出里面的第一个元素。
通过切片，则是一次取出一组连续的元素，相当于得到一个子列表

---

使用[ : ]的方式进行切片操作

a = [1,2,3,4]
print(a[1:3])

a中的[1:3]表示的是[1，3)这样由下标构成的前闭后开区间，也就是下标为1的元素开始(2)，到下标为3的元素结束(4)，但是不包含下标为3的元素。

---

切片操作中可以省略前后边界

a = [1,2,3,4]
print(f'不省略边界a = {a[1:3]}')
print(f'省略前边界a = {a[:3]}')
print(f'省略后边界a = {a[1:]}')
print(f'省略两个边界a = {a[:]}')

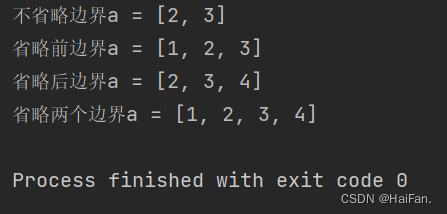
前后边界可以用负数表示吗？当然可以。

a = [1,2,3,4]
print(f'不省略边界a = {a[1:-2]}')
print(f'省略前边界a = {a[:-2]}')
print(f'省略后边界a = {a[1:]}')
print(f'省略两个边界a = {a[:]}')

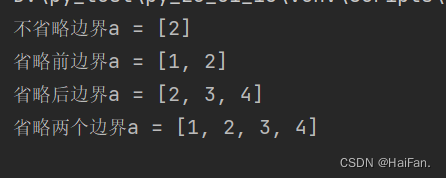
省略后边界：从开始位置，一直取到整个列表结束
省略前边界：从列表的起始元素，一直取到结束的后边界，但是不访问下标为后边界的那一个元素
省略前后边界：取出整个列表，从起始位置到结束位置。

---

切片操作还可以指定步长，也就是没访问一个一个元素后，下标自增几步

a = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
print(f'步长为1{a[::1]}')
print(f'步长为2{a[::2]}')
print(f'步长为3{a[::3]}')
print(f'步长为4{a[::4]}')
print(f'步长为5{a[::5]}')

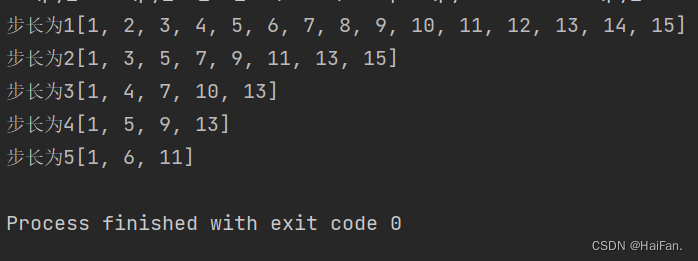
这个步长跟for循环里的range类似

---

切片操作指定的步长也可以是负数，此时是从后往前进行取元素，表示每访问一个元素之后，下标自减几步

a = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
print(f'步长为-1{a[::-1]}')
print(f'步长为-2{a[::-2]}')
print(f'步长为-3{a[::-3]}')
print(f'步长为-4{a[::-4]}')
print(f'步长为-5{a[::-5]}')

---

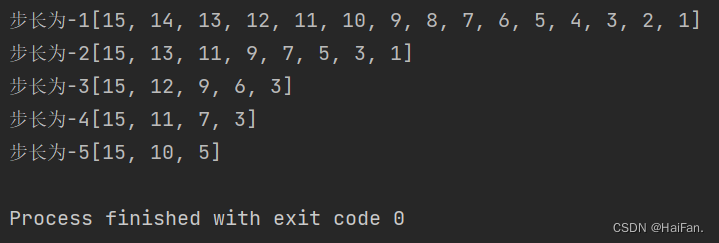
如果切片中填写的数字越界了，不会有负面效果，只会尽可能的把满足条件的元素获取到

a = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
print(a[100:2000])

---

元组和列表的这些操作都是一样的。

遍历列表元素

遍历指把元素一个一个的取出来，一般会搭配着循环使用。在以后做题的时候，会经常用到遍历。

a = [1,2,3,4,5,6]
for cnt in a:
    print(cnt)

循环中的代码，不要求必须是打印，也可以是其他操作。

---

也可以使用循环按照范围生成下标，利用下标来访问元素

a = [1,2,3,4,5,6]

for cnt in range(0,len(a)):
    print(a[cnt])

---

while循环也是可以的打印列表元素的

a = [1,2,3,4,5,6]
i = 0
while i < len(a):
    print(a[i])
    i += 1

新增元素

使用append方法，向列表末尾插入一个元素(尾插)

a = [1,2,3,4,5,6]

a.append("新年快乐")

print(a[-1])

---

使用insert方法，向任意位置插入一个元素

insert第一个参数表示要插入元素的下标

a = [1,2,3,4,5,6]

a.append("新年快乐")

a.insert(2,"新的一年也要努力学习啊")

print(a[2])

什么是方法，
方法其实就是函数，只不过函数是独立存在的，而方法往往是要依附于某个对象，像上述代码，a.insert里的insert就是依附于a的，相当于是针对a这个列表，进行插入操作。

列表的查找和删除

使用in操作符，判定元素是否存在列表中，返回值是布尔类型

a = [1,2,3,4,5,6]

print(1 in a)
print(666 in a)

---

使用index方法，查找元素在列表中的下标，返回值是一个整数，如果元素不存在，则会抛出异常

a = [1,2,3,4,5,6]

print(a.index(1))
print(a.index(100))

---

删除元素

使用pop方法删除最末尾的元素

a = [1,2,3,4,5,6]
print(len(a))
print(a[-1])
a.pop()
print(len(a))
print(a[-1])

---

pop也能按照下标来删除元素

a = [1,2,3,4,5,6]

print(a[2])

a.pop(2)

print(a[2])

---

使用remove方法，按照值删除元素

a = [1,2,3,4,5,6]

print(a[2])

a.remove(3)

print(a[2])

连接列表

使用+能够把两个列表拼接在一起

此处的+的结果是会生成一个新的列表，而不会影响到旧列表的内容

a = [1,2,3,4,5,6]
b = [7,8,9]

c = a + b
print(c)

---

使用extend方法，相当于把一个列表拼接到另一个列表的后面。

a.extend(b)是把b的内容拼接到a的末尾，不会修改b，但是会修改a

a = [1,2,3,4,5,6]
b = [7,8,9]

a.extend(b)

print(a)
print(b)

关于元组

元组和列表的功能基本是一致的。
元组使用()来表示

a = ()
b = tuple()
print(type(a))
print(type(b))

元组不能修改里面的元素，列表可以修改
像一些遍历，切片，遍历，in，index，+，等，元组一样支持。
但是像修改元素的操作，删除元素，entend等，元组不支持。

另外，元组在python中i，很多时候是默认的集合类型，如，当一个函数有多个返回值的时候。

def swap():
    return 10,11

ret = swap()
print(type(ret))

这里的ret的类型，是元组。

总结

元组和列表，就介绍到这里，
在需要多个元素的时候，可以考虑使用列表或者元组。
如果元素需要改变就先考虑用列表
如果元素不需要改变就先考虑用元组

---

最后祝大家新年快乐！！！！