文章目录
- 遍历定义
- 深度优先搜索(DFS)
- 算法步骤
- 邻接矩阵上的遍历
- 邻接矩阵深度优先算法
- DFS算法效率分析
- 广度优先搜索(BFS)
- 邻接表的广度优先算法
- BFS算法效率分析
- DFS与BFS算法效率比较
遍历定义
- 和树的遍历类似,图的遍历也是从图中的某一个顶点出发,按照某种方法对图中所有顶点访问且仅访问一次,就叫做图的遍历,它是图的基本运算。
- 图的遍历算法是求解图的连通性问题、拓扑排序和关键路径等算法的基础。
举个栗子
从景区的大门口出发,如何走才能访问且仅访问一次每一个结点,这样一个问题就可以抽象成一个图。
- 用顶点来表示每个要参观的景点。
- 用顶点之间的边来表示连个景点之间的路线。
- 将所有景点都走一遍,就是对图中所有顶点遍历的一个过程。
遍历实质:找每个顶点的邻接点的过程。
图的特点:
- 图中可能存在回路,且图的任一顶点都有可能与其他顶点相通,在访问完某个顶点之后可能沿着某些边又回到了层间访问过的顶点。
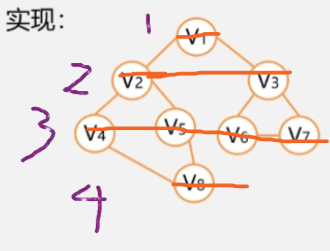
- 比如上面的图:从V1出发,依次经过了V2 V4 V8 V5 最后又回到了 V2,此时这个V2已经访问过一次,就不再访问了。
- 将访问过的顶点记录下来。
如何避免重复访问
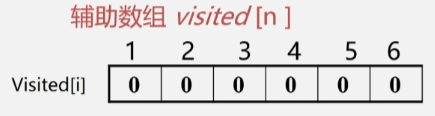
解决思路:设置辅助数组 visited[n],用来标记每个被访问过的顶点。
- 初始状态 visited[i] = 0。
- 顶点 i 被访问,则 visited[i] = 1,防止被多次访问。
深度优先搜索(DFS)
算法思想
仿树的先序遍历,一条道走到黑。
举个栗子
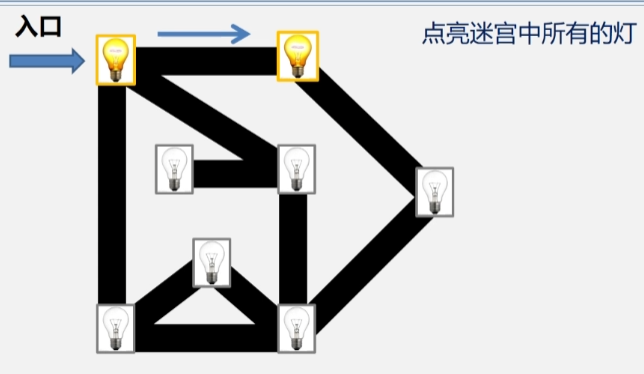
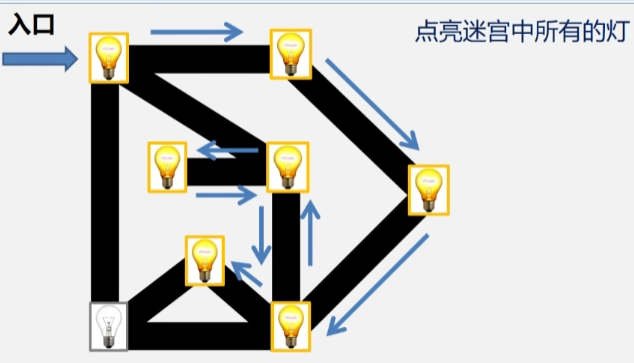
- 先点亮第一盏灯,此时发现和这盏灯连接的灯还有三盏灯,选择与之连接的一盏灯去点亮它。
>
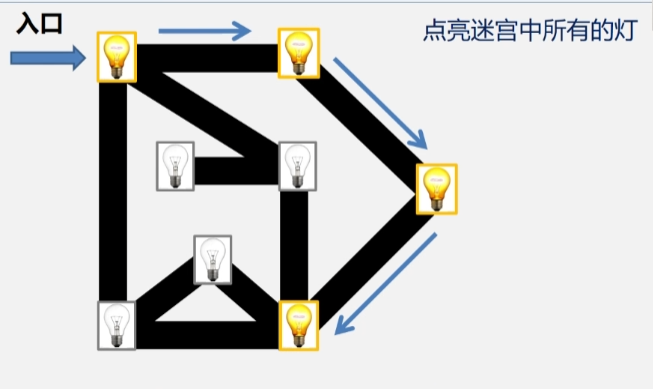
- 接下来从这盏灯出发不回去,继续按照深度遍历的方法往下访问。
- 到了有多个邻接点的顶点时,这时候发现有三盏灯可以被点亮,选择一个顶点执行深度遍历访问下去,一条道走到黑,直到不能再继续往深层走。
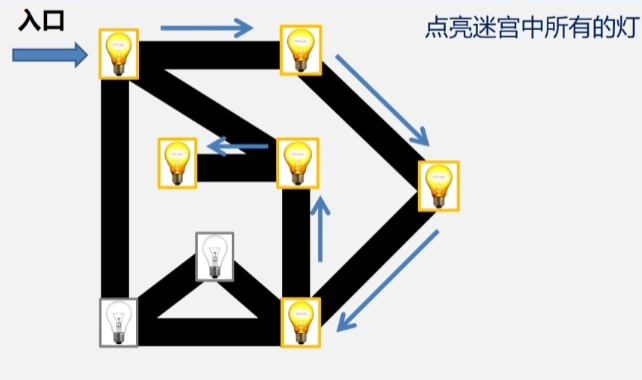
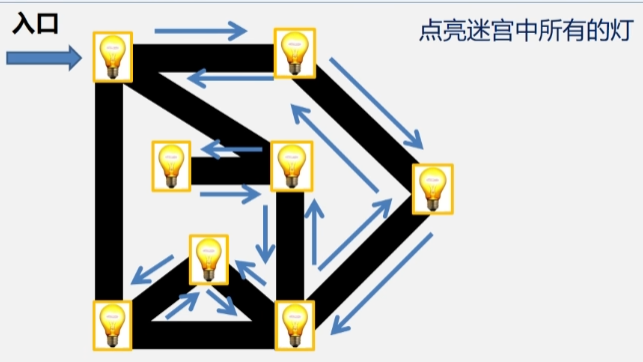
- 发现无路可走的时候,此时就回退到上一个位置看看还有没有没有被点亮的灯,如果访问过了,则继续往回退,直到发现还有没被访问过的顶点为止。.
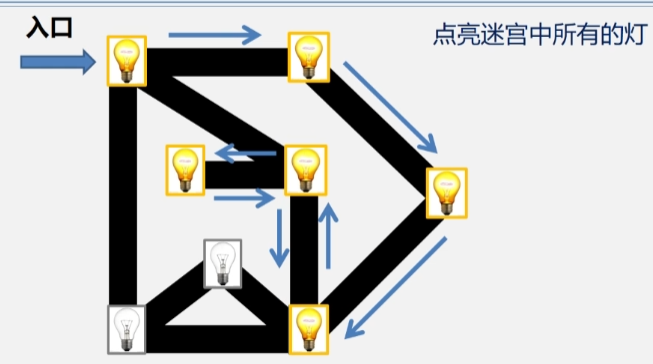
- 当退到某个顶点所邻接的顶点还有没被访问过的顶点时,继续往里走。
- 当发现顶点访问过时,则继续往回退,直到退回到起始点时,则表示遍历完毕
算法步骤
- 在访问图中某一个起始点 V,从 V出发,访问它的任一邻接顶点 W1,当有多个没有访问的邻接点可以访问时,任选其一。
- 再从 W1 出发,访问与 W1 邻接但还未被访问过的顶点 W2.
- 然后从 W2 出发,进行类似的访问…
- 如此进行下去,直到到达所有的邻接顶点都访问过的顶点 u 为止。
- 接着,回退一步,遇到前依次刚被访问过的顶点,看是否还有其他没有被访问的邻接顶点。
- 如果有:则访问此顶点,之后再从此顶点出发,进行与前面类似方法的访问。
- 如果没有:就再退回一步进行搜索。重复上述过程直到连通图汇总所有顶点都被访问过为止。
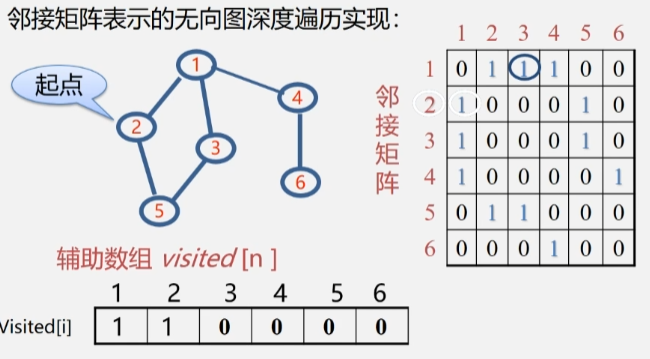
邻接矩阵上的遍历
- 深度优先搜索遍历连通图是一个递归的过程。
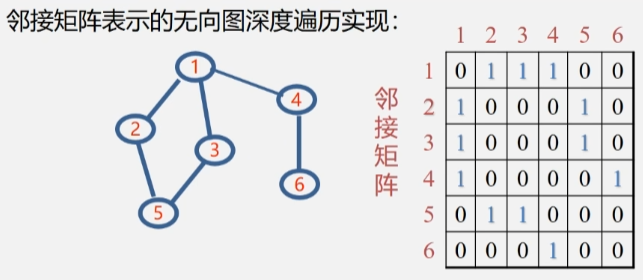
- 二维数组的第 i 行 i 列用来判断某个顶点到其他顶点之间是否有边。
- 如:第一行/列 就是判读顶点 1 到其余顶点间是否有边,V1 到 V2 V3 V4 有边记为1,其余记为 0。
- 光用邻接矩阵的话就没有办法判断某个顶点是否有被访问过,所以此时辅助数组 visited[i] 就派上用场了。
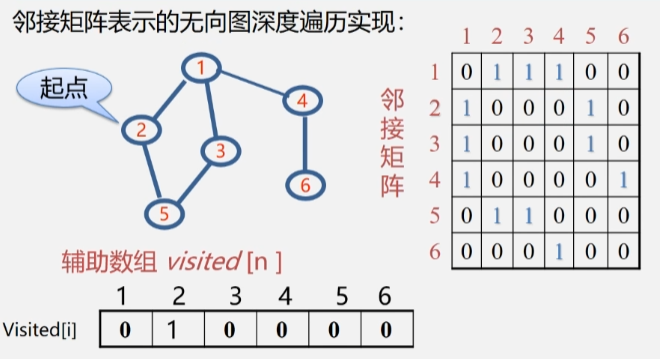
- 开始先将辅助数组内的值全部置为0,表示全都顶点都没访问过,访问过的顶点则将该顶点在辅助数组中的位置的值置为1。
- 假设起点是从顶点 2 开始,那么 2 肯定被访问过了,将 visited[2] 值置为 1。
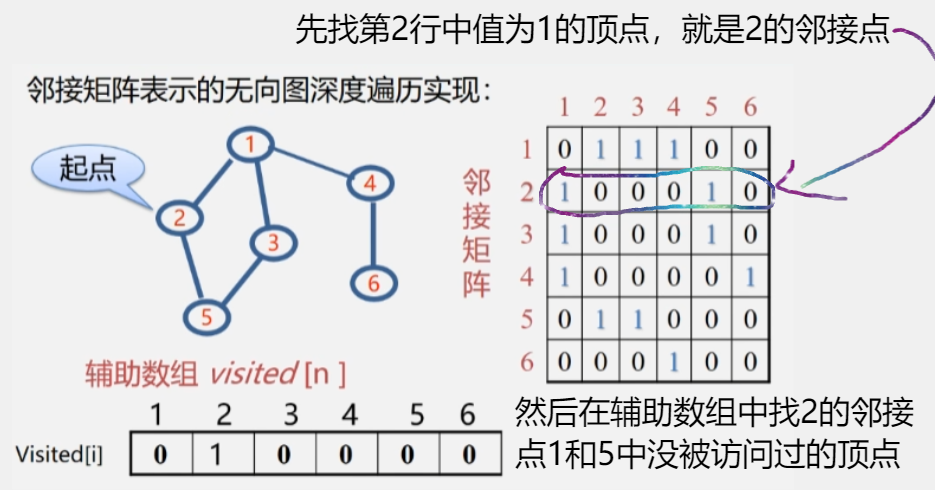
- 然后去看 2 的邻接点有哪些没被访问过,然后去访问在数组对应位置上为 0 的顶点 2 邻接点。
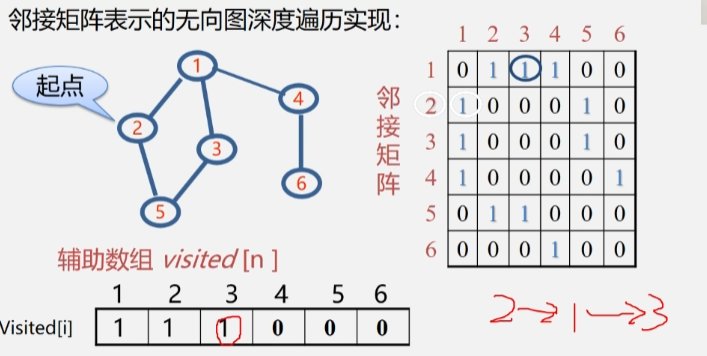
- 找邻接点:2 号顶点的邻接点都在邻接矩阵中表示出来了,在行下标为 2 的一维数组中,去找值为 1 的顶点。
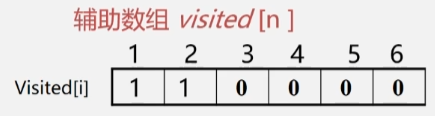
- 顶点 1 在辅助数组中的值为 0,访问它,然后将 visited[1] 的值改为1.
- 然后再从顶点 1 往下遍历,从邻接矩阵中一个一个找邻接点,然后从辅助数组中判断找出来的邻接点是否被访问过。
- 顶点1 的第一个邻接点 2 被访问过了,继续找下一个邻接点 3,发现还没被访问过,走 忽略。
- 然后将 visited[3] 置为1.
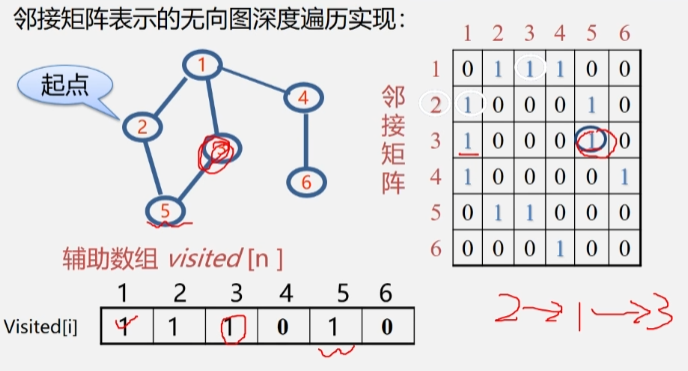
- 到了顶点 3 之后就从 3 出发继续执行深度遍历
- 从邻接矩阵中找顶点 3 的邻接点。
- 从辅助数组中判断对应的邻接点是否被访问过。
- 接下来就到了 5 号结点了,将 5 号结点的值改为 1.
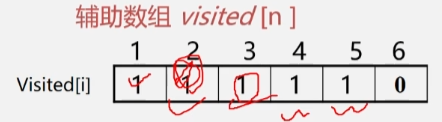
- 访问到顶点 5 时,发现它的两个邻接点都被访问过了,此时就往后退,直到退到顶点 1 时,发现顶点 1 还有个邻接点 4 没被访问过,走 忽略。
- 然后从顶点 4 开始,去访问 6 号顶点,并将 visited[6] 的值改为1.
- 到了顶点 6 时发现它的邻接点都被访问过了,此时就往后退,直到退到起点时,发现辅助数组中的元素都是1,此时遍历结束。
邻接矩阵深度优先算法
void DFS(AMGraph G,int v)//图 G 为邻接矩阵类型
{
visit(v);//访问第 v 个顶点
visited[v] = 1;访问之后立即修改辅助数组元素
for(w = 0;w < G.vexnum;w++)//从v所在行从头检索邻接点
{
//找邻接矩阵中值不为0,且辅助数组中值为0的点,然后从这个点出发继续去遍历
if((G.arcs[v][w] != 0)&&(!visited[w]))
{
DFS(G,w);//w是v的邻接带你,如果w未访问,则递归调用DFS
}
}
}
DFS算法效率分析
假设图中有 n 个顶点,e 条边
- 用邻接矩阵来表示图,遍历图中每一个顶点都要从头扫描该顶点所在行,时间复杂度是 O(n2) 。
- 用邻接表来表示图,虽然有 2e 个表结点,但只需要扫描 e 个结点即可完成遍历,加上访问 n 个头结点的时间,时间复杂度为 O(n+e)。
结论
- 稠密图适于在邻接矩阵上进行深度遍历。
- 稀疏图适于在邻接表上来进行深度遍历。
广度优先搜索(BFS)
算法思想
仿树的层次遍历,从一个顶点开始去访问它的所有邻接点。
遍历方法
- 从图中的某个顶点 V 出发。
- 依次访问该结点的所有邻接点 Vi1,Vi2,…Vin。
- 再按照这些顶点被访问的先后次序依次访问与它们相邻接的所有未被访问的顶点。
- 重复此过程,直到左右顶点均被访问为止。
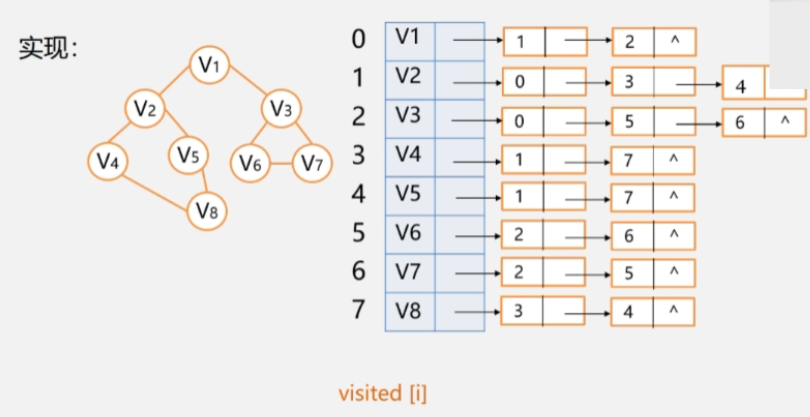
例如:
- 从顶点 V1 出发,访问 V1。
- 依次访问 V1 的各个未曾访问过的顶点 V2 和 V3。
- 依次访问 V2 的邻接点 V4 和 V5 ,以及 V3 的邻接点 V6 和 V7,最后访问 V4 的邻接点 V8。
- 由于这些顶点的邻接点均已被访问,并且图中所有的顶点都被访问,由此完成了图的遍历。得到的顶点访问序列为: V1->V2->V3->V4->V5->V6->V7->V8
再看个栗子
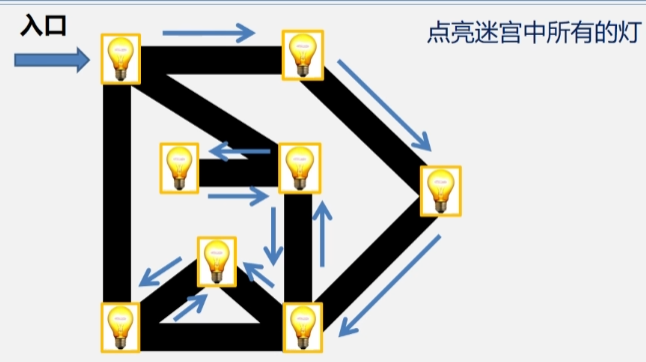
- 首先点亮入口处的灯,然后依次去点亮与这盏灯灯邻接的其余灯。
- 全部点亮之后再扩大一层,从这三盏灯开始,点亮与这三盏灯邻接的其余灯.
邻接表的广度优先算法
使用邻接表来进行遍历,任然需要一个辅助数组 visited[i] 来记录被访问的顶点。
访问一个点,然后接下来去访问它的邻接点,再然后去访问邻接点的邻接点,类似于树的层次遍历。
- 既然遍历方法类似于树的层次遍历,那么算法当然也可以。
算法步骤
广度优先算法需要借助队列
- 从图中某个顶点 V 出发,访问 V,并将visited[V] 的值置为1,然后将 V 进队。
- 只要队列不为空,则重复以下操作。
- 队头顶点 u 出队,
- 依次检查 u 的所有邻接点 w,如果visited[w] 的值为 0,则访问 w,并将 visited[w] 的值置为1,然后将 w 进队。
算法实现
//按照广度优先非递归遍历连通图 G
void BFS(Graph G,int v)
{
cout << v;visited[v] = 1;//访问第v个顶点,并修改辅助数组对应位置的值为1
InitQueue(Q);//将辅助队列Q初始化,置空
EnQueue(Q,v);//将v进队
while(!QueueEmpty(Q));//队列非空
{
DeQueue(Q,u);//将对头元素出队并置为u
//依次检查 u 的所有邻接点 w,FirstAdjVex(G,u)表示u的第一个邻接点
//NextAdjVex(G,u,w)表示u相对于w的下一个邻接点,w>=0表示存在邻接点
for(W = FirstAdjVex(G,u);w >= 0;w = NextAdjVex(G,uw))
{
if(!visited[w])//w为u的尚未访问的邻接顶点
{
cout << w;//访问w
visited[w] = 1;//将w在辅助数组中的值为1
EnQueue(Q,w);//将w进队
}
}
}
}
BFS算法效率分析
假设图中有 n 个顶点,e 条边
- 如果使用邻接矩阵,则BFS对一每一个被访问到的顶点,都要循环检测矩阵中国的整整一行(n 个元素),总的时间代价为 O(n2)。
- 用邻接表来表示图,虽然有 2e 个表结点,但是只需要扫描e个结点即可完成遍历,加上访问 n 个头结点的时间,时间复杂度为 O(n+e)。
DFS与BFS算法效率比较
- 空间复杂度相同,都是 O(n)(借用了堆栈和队列)。
- 时间复杂度只与存储结构(邻接矩阵和邻接表)有关,而与搜索路径无关。