力扣98.验证二叉搜索树

题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true
示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

算法思路

基于二叉搜索树的性质：中序遍历一棵二叉搜索树将获得一个递增序列
采用中序遍历的思路，对该二叉树进行中序遍历，每次遍历到的值与前一次遍历到的值比较，如果不是递增的，就返回false表示这不是一棵二叉搜索树
时间复杂度O(n)

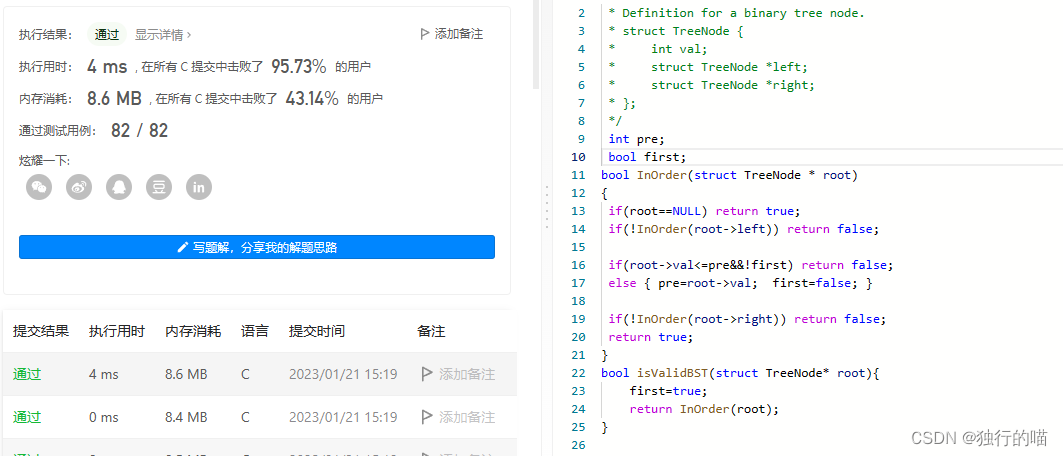
代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
 int pre;//前一次遍历到的值
 bool first;//是否是第一次遍历的标志
bool InOrder(struct TreeNode * root)
{
 if(root==NULL) return true; 
 if(!InOrder(root->left)) return false;//若左子树不是二叉搜索树，返回false；

 if(root->val<=pre&&!first) return false;//若当前遍历的值没有比前一个大，返回false
 else { pre=root->val;  first=false; }//更新pre
 
 if(!InOrder(root->right)) return false;//若右子树不是二叉搜索树，返回false；
 return true;
}
bool isValidBST(struct TreeNode* root){
    first=true;
    return InOrder(root);
}