在普通 PID 控制中引入积分环节的目的，主要是为了消除静差，提高控制精度。但在过程的启动、结束或大幅度增减设定时，短时间内系统输出有很大的偏差，会造成PID运算的积分积累，致使控制量超过执行机构可能允许的最大动作范围对应的极限控制量，引起系统较大的超调，甚至引起系统较大的振荡。这在生产中是绝对不允许的。
积分分离控制基本思路是:当被控量与设定值偏差较大时，取消积分作用，以免由于积分作用使系统稳定性降低，超调量增大;当被控量接近给定值时，引入积分控制，以便消除静差，提高控制精度。其具体实现步骤如下:
(1)根据实际情况,人为设定阈值>0;
(2）当|error(k) |>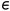 
时，采用PD控制，可避免产生过大的超调，又使系统有较快的响应;
(3）当|error(k)|≤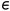时，采用PID控制，以保证系统的控制精度。
积分分离控制算法可表示为：
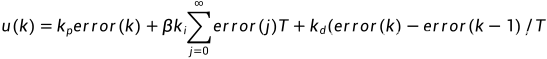
式中，T为采样时间；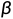
为积分项的开关系数。
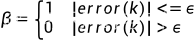
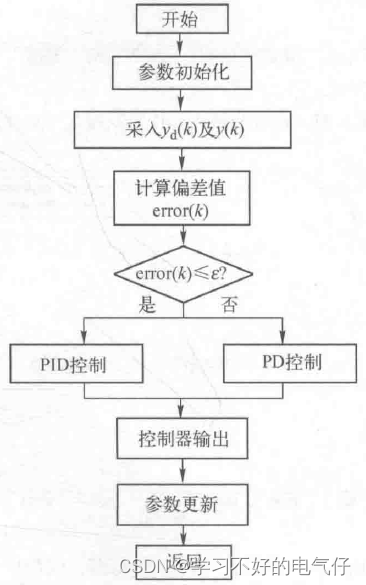
根据积分分离式PID控制算法得到其程序框图如图所示。
例：
设被控对象为一延迟对象：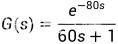
采样时间为20s，延迟时间为4个采样时间，即80s，被控对象离散化为：
y(k)=-den(2)y(k -1)+ num(2)u(k-5)
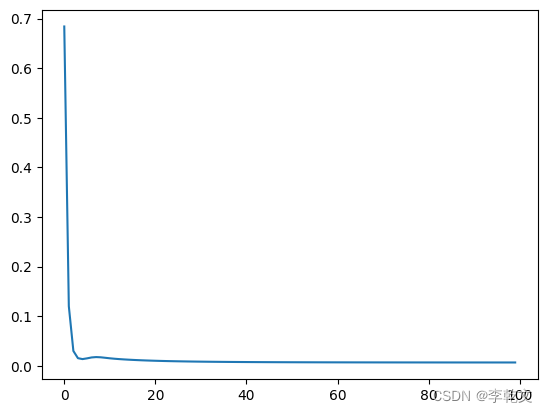
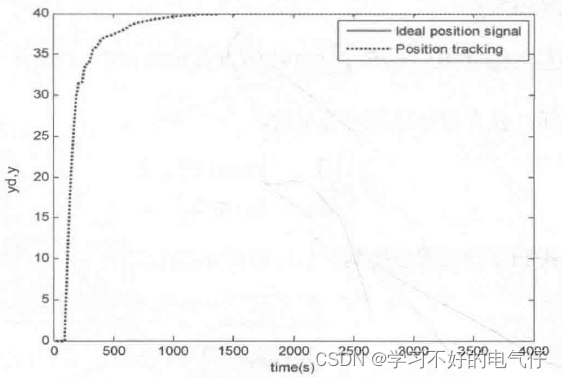
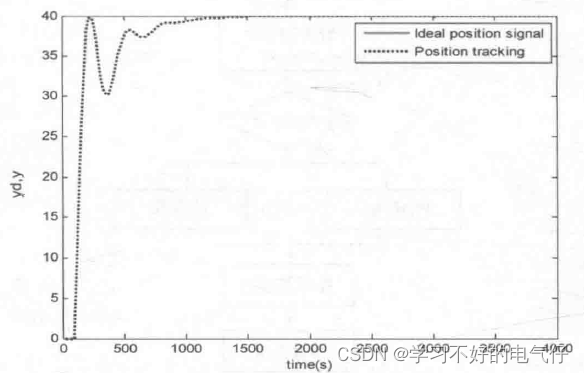
取M=1，采用积分分离式 PID控制器进行阶跃响应，对积分分离式PID控制算法进行改进，采用分段积分分离方式，即根据误差绝对值的不同，采用不同的积分强度。仿真中指令信号为y,(k)=40，控制器输出限制在[-110,110]，其阶跃式跟踪结果如图所示。取M=2，采用普通PID控制，其阶跃式跟踪结果如图所示。
仿真程序：
%Integration Separation PID Controller
clear all;
close all;
ts=20;
%Delay plant
sys=tf([1].[60,1],"inputdelay',80);
dsys=c2d(sys,ts,'zoh');
[num,den]=tfdata(dsys,'V);
u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;
y_1=0;y_2=0;y3=0;
error_1=0;error 2=0;
ei=0;
for k=1:1:200
time(k)=k*ts;
%Delay plant
y(k)=-den(2)*y_1+num(2)*u_5;
%l separation
yd(k)=40;
error(k)=yd(k)-y(k);
ei=ci+error(k)*ts;
M=2;
if M==1
%Using integration separation
if abs(error(k))>=30
beta=0.0;
clseif abs(error(k))>=20&abs(error(k))-30
beta=0.6;
elseif abs(error(k))>-10&abs(error(k))<-20
beta=0.9;
else
beta=1.0;end
elseif M==2
beta=1.0； %Not using integration separation
end
kp=0.80;
ki=0.005;
kd=3.0;
u(k)=kp*error(k)+kd*(error(k)-error_1)/ts+beta*ki*ei;
if u(k)>=110 % Restricting the output of controller
u(k)=110;
endif u(k)<=-110
u(k)=-110;
end
u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_l;u_1=u(k);
y_3=y_2;y_2=y_1；y_1=y(k);
error_2=error_l;
error_1=error(k);
end
figure(1);
plot(time,yd,'r,time,y,'k:'. linewidth',2);
xlabel('time(s)');ylabel('yd,y);
legend('Ideal position signal','Position tracking');
figure(2);
plot(time,u,'t,linewidth',2);
xlabel('time(s)');ylabel('Control input');
由仿真结果可以看出，采用积分分离方法控制效果有很大的改善。值得注意的是，为保证引入积分作用后系统的稳定性不变，在输入积分作用时比例系数k可作相应变化。此外，β值应根据具体对象及要求而定，若β过大，则达不到积分分离的目的;若β过小,则会导致无法进入积分区。如果只进行PD控制，会使控制出现余差。
