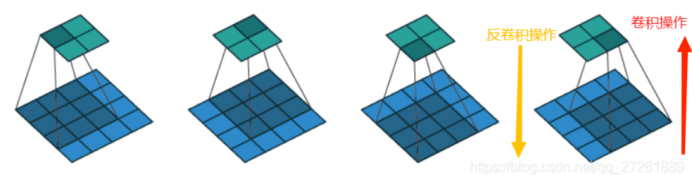
上图是一个卷积操作（蓝色为输入，绿色为输出）。

输入的特征图为x：( 4，4 ，channels_in）其中channels_in表示通道数。

卷积核设置：无padding， kernel size为3*3， 步长stride 为1,

输出的特征图为y，(2 ,2  channels_out)，channels_out也是通道数。

逆卷积操作就是跟卷积操作的输入输出正好相反（绿色是输入，蓝色是输出）。输入变为特征图y, 卷积核设置同上。输出是上面的特征图x。

再来看一个例子（蓝色为输入，绿色为输出）：

我们可以这样想，蓝色的特征图是经过encoder不断卷积后的图片，我们现在要做的是将其尺寸放大，channel数量也变大。这时，就需要用到nn.ConvTranspose2d了。

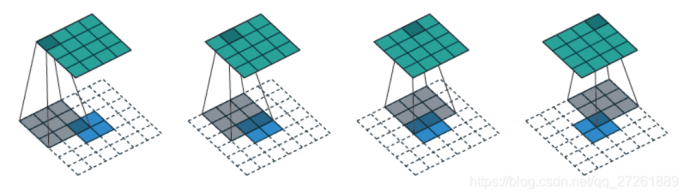
这里说一下这个新的特征图是怎么得到的：我们在输入的特征图基础加上一些东西，专业名词叫做interpolation，也就是插值。

这就涉及到两个问题，①插在哪里，②插什么。

插什么？插的就是0。

插在哪里？在原先高度方向的每两个相邻中间插上"S t r i d e − 1 Stride-1Stride−1"。

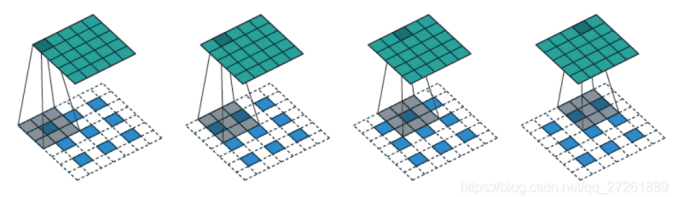
对图的说明（蓝色为输入，绿色为输出）：

输入特征图A：(3,3,in_channel)

输入卷积核K：kernel为3 ∗ 3 3*33∗3， stride为2， padding为1

新的特征图B： 3 + ( 3 − 1 ) ∗ ( 2 − 1 ) = 3 + 2 = 5 3 + (3-1)*(2-1) = 3+2 = 53+(3−1)∗(2−1)=3+2=5