复合类型与结构体
数据抽象
数据类型标志
嵌套结构体
复合类型与结构体
在编程语言中,最基本的,不可再分的数据类型称为基本类型,例如整型,浮点型;根据语法规则由基本类型组合而成的类型称为复合类型,例如字符串是由很多字符组成的。有些场合下要把复合类型当作一个整体来用,而另外一些场合下需要分解组成这个复合类型的各种基本类型,复合类型的这种两面性为数据抽象奠定了基础。在学习一门编程语言时要特别注意以下三个方面:
1.这门语言提供了哪些Primitive,比如基本类型,比如基本运算符,表达式和语句。
2.这门语言提供了哪些组合规则,比如基本类型如何组成复合类型,比如简单的表达式和语句如何组成复杂的表达式和语句。
3.这门语言提供了哪些抽象机制,包括数据抽象和过程抽象
本章以结构体为例讲解数据类型的组合和数据抽象。至于过程抽象,我们在if/else语句已经见过最简单的形式,就是把一组语句用一个函数名封装起来,当作一个整体使用,本章节将介绍更复杂的过程抽象。
现在我们用C语言表示一个复数,从直角坐标系来看,复数由实部和虚部组成,从极坐标系来看,复数由模和幅角组成,两种坐标系可以相关转换。
如果用实部和虚部表示一个复数,我们可以写成由两个double型组成的结构体:
struct complex_struct {
double x, y;
};这一句定义了标识符complex_struct,这种标识符在C语言中称为Tag,struct complex_struct{double x,y;} ;整个可以看作一个类型名,就像int或double一样,只不过它是一个复合类型,如果用这个类型名来定义变量,可以这样写:
struct complex_struct {
double x, y;
} z1, z2;这样z1和z2就是两个变量名,变量名定义后面带个;号是我们早已经习惯的。但即使像先前的例子那样只定义complex_struct这个Tag而不定义变量,}后面的;号也不能少。这一点一定要注意,类型定义也是一种声明,声明都要以;号结尾,结构体类型定义的}后面少;号是初学者常犯的错误。不管是用上面两种形式的哪一种定义了complex_struct这个Tag,以后都可以直接用struct complex_struct来代替类型名了。例如可以这样定义另外两个复数变量:
struct complex_struct z3, z4;如果在定义结构体类型的同时定义了变量,也可以不写Tag,例如:
struct {
double x, y;
} z1, z2;但这样就没办法再次引用这个结构体类型了,因为它没有名字。每个复数变量都有两个成员x和y,可以用.运算符来访问,这两个成员的存储空间是相邻的,合在一起组成复数变量的存储空间。
定义和访问结构体
int main()
{
struct complex_struct { double x, y; }z;
double x = 3.0;
z.x = x;
z.y = 4.0;
if (z.y > 0)
{
printf("z.x=%f z.y=%f\n", z.x, z.y);
}
else {
printf("error");
}
return 0;
}注意上例中的变量x和变量z的成员x的名字并不冲突,因为变量z的成员x只能通过表达式z.x来访问,编译器可以从语法上来区分哪个x是变量x,哪个x是变量z的成员x,这里在后面的章节变量的存储布局中会讲到这两个标识符x属于不同命名空间。结构体Tag也可以定义在全局作用域中,这样定义的Tag在其定义之后的函数中都可以使用。例如:
struct complex_struct { double x, y; };
int main(void)
{
struct complex_struct z;
....
}结构体变量也可以在定义时初始化,例如:
struct complex_struct z = { 3.0, 4.0 };Initializer中的数据依次赋给结构体的各成员。如果Initializer中的数据比结构体的成员多,编译器会报错,但如果只是末尾多个逗号则不算错。如果Initializer中的数据比结构体的成员少,未指定的成员将用0来初始化,就像未初始化的全局变量一样。例如以下几种形式的初始化都是合法的:
double x = 3.0;
struct complex_struct z1 = { x, 4.0, }; /* z1.x=3.0, z1.y=4.0 */
struct complex_struct z2 = { 3.0, }; /* z2.x=3.0, z2.y=0.0 */
struct complex_struct z3 = { 0 }; /* z3.x=0.0, z3.y=0.0 */注意,z1必须是局部变量才能用另一个变量x的值来初始化它的成员,如果是全局变量就只能用常量表达式来初始化。这也是C99的新特性,C89只允许在{}中使用常量表达式来初始化,无论是初始化全局变量还是局部变量。
{}这种语法不能用于结构体的赋值,例如这样是错误的:
struct complex_struct z1;
z1 = { 3.0, 4.0 };以前我们初始化基本类型的变量所使用的Initalizer都是表达式,表达式当然也可以用来赋值,但现在这种由{}括起来的Initalizer并不是表达式,所以不能用来赋值。
Initializer->表达式
Initalizer->{初始化列表}
初始化列表->Designated-lnitializer,Designated-Initializer....
Designated-lnitializer->Initializer
Designated-lnitializer->.标识符=Initalizer
Designated-lnitializer->[常量表达式]=Initalizer
Designated-lnitializer是C99引入的新特性,用于初始化稀疏结构体和稀疏数组很方便。有些时候结构体或数组中只有某一个或某几个成员需要初始化,其他成员都用0初始化即可,用Designated Initializer语法可以针对每个成员做初始化,很方便。
struct complex_struct z1 = { .y = 4.0 }; /* z1.x=0.0, z1.y=4.0 */数组的Memberwise Initialization语法将在下一张介绍。
结构体类型用在表达式中有很多限制,并不像基本类型那么自由,比如+-*/等算术运算符和&&||!等逻辑运算符都不能作用于结构体类型,if语句,while语句中的控制表达式的值也不能是结构体类型。严格来说,可以做算术运输的类型称为算术类型,算术类型包括整型和浮点型。可以表示零和非零,可以参与逻辑与,或,非运算或者做控制表达式的类型称为标量类型,标量类型包括算术类型和以后要讲的指针类型。
结构体变量之间用赋值运算符是允许的,用一个结构体变量初始化另一个结构体变量也是允许的,例如:
struct complex_struct z1 = { 3.0, 4.0 };
struct complex_struct z2 = z1;
z1 = z2;同样地,z2必须是局部变量才能用变量z1的值来初始化。既然结构体变量之间可以相互赋值和初始化,也就可以当作函数的参数和返回值来传递:
struct complex_struct add_complex(struct complex_struct z1, struct
complex_struct z2)
{
z1.x = z1.x + z2.x;
z1.y = z1.y + z2.y;
return z1;
}这个函数实现了两个复数相加,如果在main函数中这样调用:
struct complex_struct z = { 3.0, 4.0 };
z = add_complex(z, z);那么调用传参的过程如下图所示:
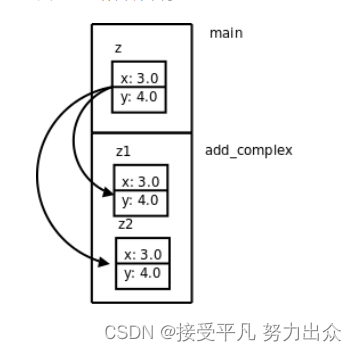
变量z在main函数的栈帧上,参数z1和z2在add_complex函数的栈帧上,z的值分别赋给z1和z2。在这个函数里,z2的实部和虚部被累加到z1中,然后return z1;可以看成是:
1.用z1初始化一个临时变量
2.函数返回并释放栈帧
3.把临时变量的值赋给变量z,并释放临时变量。
由.运算符组成的表达式能不能做左值取决于.运算符左边的表达式能不能做左值。在上面的例子中,z是一个变量,可以做左值,因此表达式z.x也可以做左值,但表达式add_complex(z,z).x只能做右值而不能做左值,因此表达式add_complex(z,z)不能做左值。
数据抽象
现在我们来实现一个完整的复数运算程序。在上一节我们已经定义了复数的结构体类型,现在需要围绕它定义一些函数。复数可以用直角坐标或极坐标表示,直角坐标做加减法比较方便,极坐标做乘除法比较方便。如果我们定义的复数结构体是直角坐标的,那么应该提供极坐标的转换函数,以便在需要的时候可以方便地取它的模和副角:
#include <math.h>
struct complex_struct {
double x, y;
};
double real_part(struct complex_struct z)
{
return z.x;
}
double img_part(struct complex_struct z)
{
return z.y;
}
double magnitude(struct complex_struct z)
{
return sqrt(z.x * z.x + z.y * z.y);
}
double angle(struct complex_struct z)
{
return atan2(z.y, z.x);
}此外,我们还应该提供两个函数用来构造复数变量,既可以提供直角坐标也可以提供极坐标,在函数中自动做相应的转换然后返回构造的复数变量:
struct complex_struct make_from_real_img(double x, double y)
{
struct complex_struct z;
z.x = x;
z.y = y;
return z;
}
struct complex_struct make_from_mag_ang(double r, double A)
{
struct complex_struct z;
z.x = r * cos(A);
z.y = r * sin(A);
return z;
}在此基础上就可以实现复数的加减乘除运算:
struct complex_struct add_complex(struct complex_struct z1, struct
complex_struct z2)
{
return make_from_real_img(real_part(z1) + real_part(z2),
img_part(z1) + img_part(z2));
}
struct complex_struct sub_complex(struct complex_struct z1, struct
complex_struct z2)
{
return make_from_real_img(real_part(z1) - real_part(z2),
img_part(z1) - img_part(z2));
}
struct complex_struct mul_complex(struct complex_struct z1, struct
complex_struct z2)
{
return make_from_mag_ang(magnitude(z1) * magnitude(z2),
angle(z1) + angle(z2));
}
struct complex_struct div_complex(struct complex_struct z1, struct
complex_struct z2)
{
return make_from_mag_ang(magnitude(z1) / magnitude(z2),
angle(z1) - angle(z2));
}可以看出,复数加减乘除运算的实现并没有直接访问结构体complex_struct的成员x和y,而是把它看成一个整体,通过调用相关函数来取它的直角坐标和 极坐标。这样就可以非常方便的替换掉结构体complex_struct的存储表示,例如改为用极坐标来存储:
#include <math.h>
struct complex_struct {
double r, A;
};
double real_part(struct complex_struct z)
{
return z.r * cos(z.A);
}
double img_part(struct complex_struct z)
{
return z.r * sin(z.A);
}
double magnitude(struct complex_struct z)
{
return z.r;
}
double angle(struct complex_struct z)
{
return z.A;
}
struct complex_struct make_from_real_img(double x, double y)
{
struct complex_struct z;
z.A = atan2(y, x);
z.r = sqrt(x * x + y * y);
}
struct complex_struct make_from_mag_ang(double r, double A)
{
struct complex_struct z;
z.r = r;
z.A = A;
return z;
}虽然结构体complex_struct的存储表示做了这样的改动,add_complex,sub_complex,mul_complex,div_complex这几个复数运算的函数却不需要做任何改动,仍然可以用,原因在于这几个函数只把结构体complex_struct当作一个整体来使用,而没有直接访问它的成员,因此也不依赖于它有哪些成员。我们结合一下图具体分析。
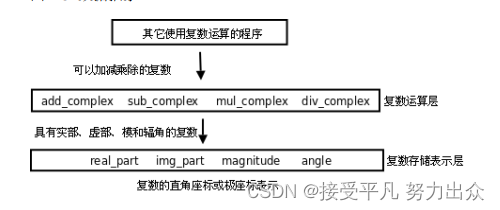
这里是一种抽象的思想。其实抽象这个概念并没有这么抽象,简单的说就是"提取公因式":ab+ac=a(b+c),如果a变了,ab和ac这两项都要改,但如果写成a(b+c)形式就只需要改动其中一个因子就行。
在我们的复数运算程序中,复数有可能用直角坐标或极坐标来表示,我们把这个有可能变动的因素提取出来组成复数存储表示层。这一层看到的数据是结构体的两个成员x和y,或者r和A,如果改变了结构体的实现就要改变这一层函数的实现,但函数接口不改变,因此调用这一层函数接口的复数运算层也不需要改变。复数运算层看到的数据只是一个抽象的"复数"的概念,知道它有直角坐标和极坐标,可以调用复数存储表示层的函数得到这些坐标。再往上看,其他使用复数运算的程序看到的数据时一个更为抽象的"复数"的概念,只知道它是一个数,像整数,小数一样可以加减乘除,甚至连他有直角坐标和极坐标也不需要知道。
这里的复数存储表示层和复数运算层称为抽象层,从底层往上层来看,复数越来越抽象了,把所有这些层组合在一起就是一个完整的系统。组合使得系统可以任意复杂,而抽象使得系统的复杂性可以控制,任何改动都只局限在某一层,而不会涉及到整个系统。
数据类型标志
在上一节中,我们通过一个复数存储表示抽象层把complex_struct结构体的存储格式和上层的复数运算函数隔开,complex_struct结构体既可以采用直角坐标也可以采用极坐标存储。但有时候需要同时支持两种存储格式,比如先前已经采集了一些数据存在计算机中,有些数据是以极坐标存储的,有些数据是以直角坐标存储的,如果要把这些数据都存到complex_struct结构体中怎么办?一种方法就是规定complex_struct结构体采用直角坐标格式,直角坐标的数据可以直接存入complex_struct结构体,而极坐标的数据先转成直角坐标再存,但由于浮点数的精度有限,,转换总是会损失精度的。这里介绍一种方法,complex_struct结构体由一个数据类型标志和两个浮点数组成,如果数据类型标志为0,那么两个浮点数就表示直角坐标,如果数据类型标志为1,那么两个浮点数就表示极坐标。这样,直角坐标和极坐标的数据都可以适配到complex_struct结构体中,无需转换和损失精度:
enum coordinate_type { RECTANGULAR, POLAR };
struct complex_struct {
enum coordinate_type t;
double a, b;
};enum关键字的作用和struct关键字类似,把coordinate_type这个标识符定义为一个Tag,struct complex_struct表示一个结构体类型,而enum_coordinate_type表示一个枚举类型。枚举类型的成员是常量,他们的值由编译器自动分配,例如定义了上面的枚举类型之后,RECTANGULAR就表示常量0,POLAR表示常量1.如果不希望从0开始分配,可以这样定义:
enum coordinate_type { RECTANGULAR = 1, POLAR };这样,RECTANGULAR就表示常量1,而POLAR就表示常量2.枚举常量也是一种整型,其值在编译时确定,因此也可以出现在常量表达式中,可以用于初始化全局变量或者作为case分支的判断条件。
有一点需要注意,虽然结构体的成员名和变量名不在同一个命名空间中,但枚举的成员名却和变量名在同一个命名空间中,所以会出现命名冲突。例如这样是不合法的:
int main(void)
{
enum coordinate_type { RECTANGULAR = 1, POLAR };
int RECTANGULAR;
printf("%d %d\n", RECTANGULAR, POLAR);
return 0;
}complex_struct结构体的格式变了,就需要修改复数存储表示层的函数,但只要保持函数接口不变就不会影响到上层函数。例如:
struct complex_struct make_from_real_img(double x, double y)
{
struct complex_struct z;
z.t = RECTANGULAR;
z.a = x;
z.b = y;
return z;
}
struct complex_struct make_from_mag_ang(double r, double A)
{
struct complex_struct z;
z.t = POLAR;
z.a = r;
z.b = A;
return z;
}嵌套结构体
结构体也是一种递归定义:结构体的成员具有某种数据类型,而结构体本身也是一种数据类型。换句话说,结构体的成员可以是另一种结构体,即结构体可以嵌套定义。例如我们在复数的基础上定义复平面上的线段:
struct segment {
struct complex_struct start;
struct complex_struct end;
}从复合类型与结构体讲的语法可以看出,Initalizer也可以嵌套,因此嵌套结构体可以嵌套地初始化,例如:
struct segment s = {{ 1.0, 2.0 }, { 4.0, 6.0 }};也可以平坦地初始化,例如:
struct segment s = { 1.0, 2.0, 4.0, 6.0 };甚至可以把两种方式混合使用:
struct segment s = {{ 1.0, 2.0 }, 4.0, 6.0 };利用C99的新特性也可以做Memberwise Initialization,例如
struct segment s = { .start.x = 1.0, .end.x = 2.0 };访问嵌套结构体的成员要用到多个.运算符,例如:
s.start.t = RECTANGULAR;
s.start.a = 1.0;
s.start.b = 2.0;