标量
简单操作

长度
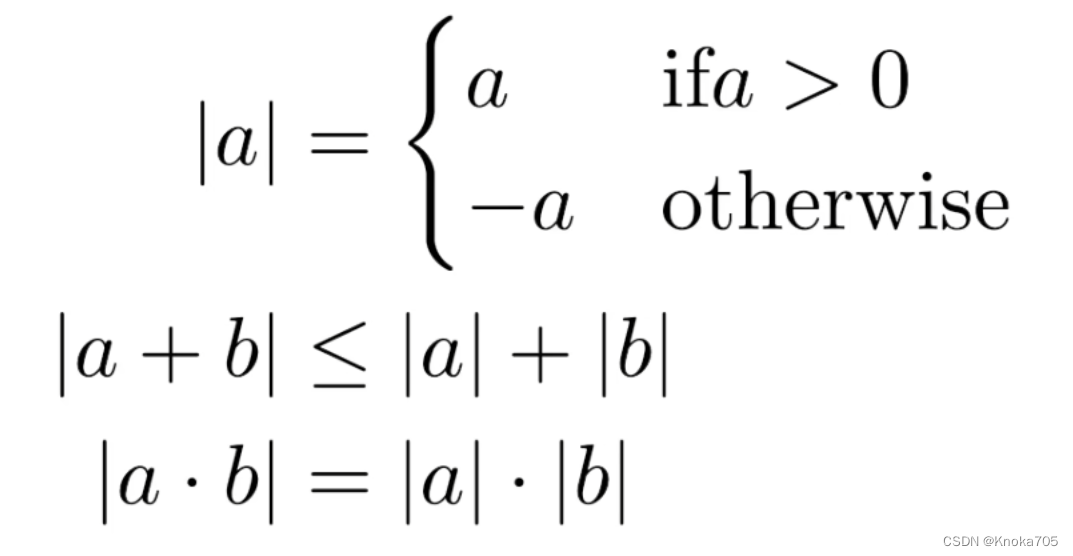
向量
简单操作


长度

其他操作

矩阵
简单操作

乘法(矩阵*向量)

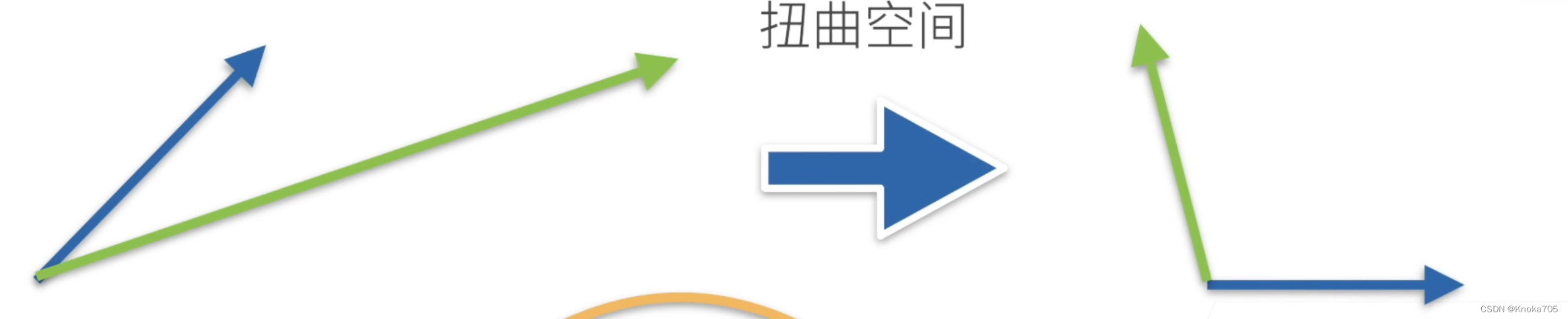
乘法(矩阵*矩阵)

范数

取决于如何衡量b和c的长度
常见范数
矩阵范数:最小的满足的上面公式的值
Frobenius范数

特殊矩阵
对称和反对称

正定

正交矩阵

置换矩阵

特征向量和特征值
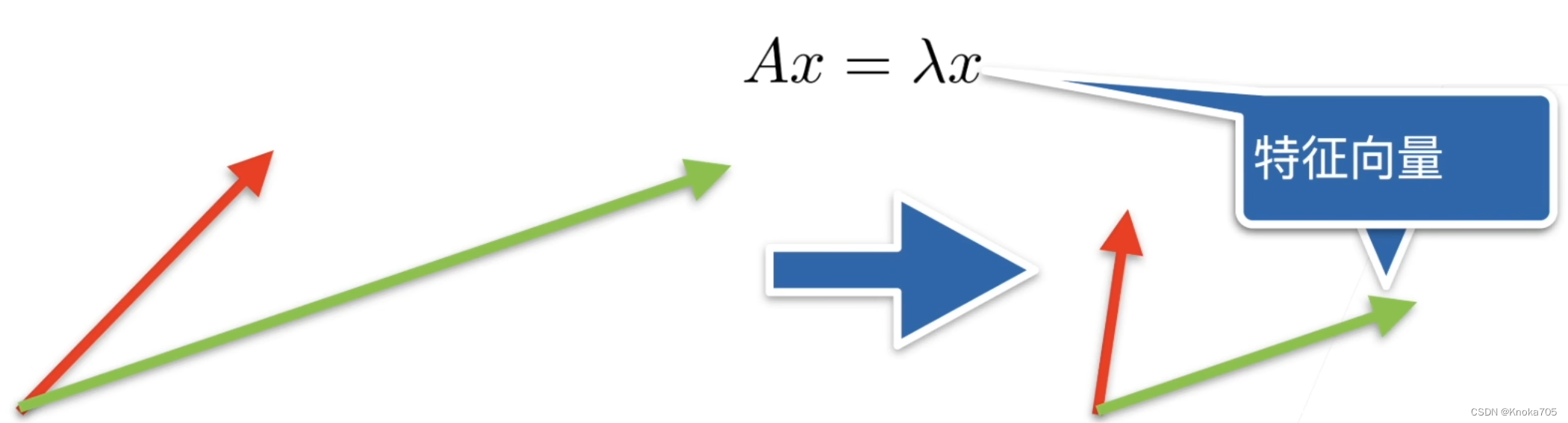
不被矩阵改变方向的向量
对称矩阵总是可以找到特征向量
线性代数实现
标量由只有一个元素的张量表示

可以将向量视为表标量值组成的列表

通过张量的索引来访问任一元素

访问张量的长度

只有一个轴的张量,形状只有一个元素

通过指定两个分量m和n来创建一个形状为m*n的矩阵

矩阵的转置

对称矩阵A等于其转置
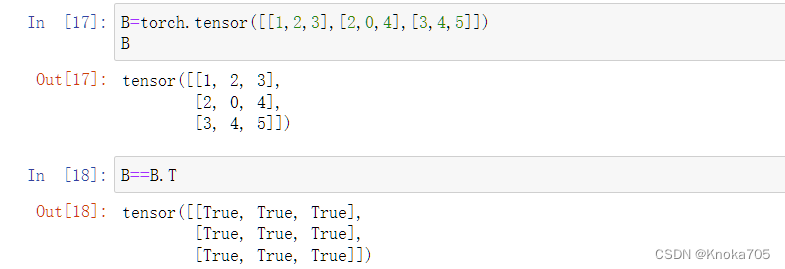
可以构建具有更多轴的数据结构

给定具有任何形状的两个张量,任何按元素二元运算的结果都将是相同形状的张量

两个矩阵的按元素乘法称为哈达玛积

计算其元素的和

表示任意形状张量的元素和

指定求和汇总张量的轴
维度原本是(2, 5, 4),按axis=0求和,即按第一个维度求和,结果维度就是(5, 4)

维度原本是(2, 5, 4),按axis=1求和,即按第二个维度求和,结果维度就是(2, 4)

也可以同时指定两个维度

一个与求和相关的量是 平均值

计算总和或均值时候保持轴数不变

通过广播将A除以sum_A

某个轴计算A元素的累积总和

点积是相同位置的按元素乘积的和

可以通过执行按元素乘法,然后进行求和来表示两个向量的点积

矩阵向量积Ax是一个长度为m的列向量

可以将矩阵-矩阵乘法AB看做是简单的执行m次矩阵-向量积,并将结果拼接在一起,形成一个n*m的矩阵

范数
L1范数

L2范数

矩阵

注意有无keepdims=True的区别