一、前言

本文主要讲了BFS如何判重和双向广搜。

二、BFS判重

BFS = 队列
BFS：逐步扩展下一层，把扩展出的下一层状态放进队列中处理。
如果这些状态有相同的，只需搜一次，只需要进入队列一次。
必须判重。

Python 判重方法：set、字典

1、set 判重

set() 函数创建一个无序、不重复元素集
关系测试，删除重复数据，计算交集、差集、并集、补集。

a=set()
a.add("678");print(a)
a.add("123");print(a)
a.add("678")    #第二个"678"加不进集合了
print(a)
b=sorted(a);print(b);print()
s=set("aabc");print(s);print()  #a,b,c的输出顺序不定的,输出 {'a','b','c'}
s=set(["aabc","bca"]);print(s);print()      #输出{"aabc","bca"}

b=set()
b.add(678);print(b)
b.add(123);print(b)
b.add(678);print(b);print()

a=set([1,1,2,3,5]);print(a)
b=set([1,2,3,4]);print(b)
print(a-b)  #差，在集合a中但不在集合b中的元素
print(b-a)  #差
print(a&b)  #交，同时在集合a和b中的共同元素
print(a|b)  #并，包括集合a和b中所有元素

2、字典判重

字典：无序、可变、有索引的集合。
字典：用花括号定义，有键和值。

a={5:"xy"}
a[1]="cb"
a[2]="kd"
a[2]="af"
print(a);print()

b=sorted(a.items());print(b)
b=sorted(a.items(),key=lambda x:x[0]);print(b)  #按键排序
b=sorted(a.items(),key=lambda x:x[1]);print(b)  #按值排序
print()

a={"food":"xy","price":555}
a[3]=899
print(a)

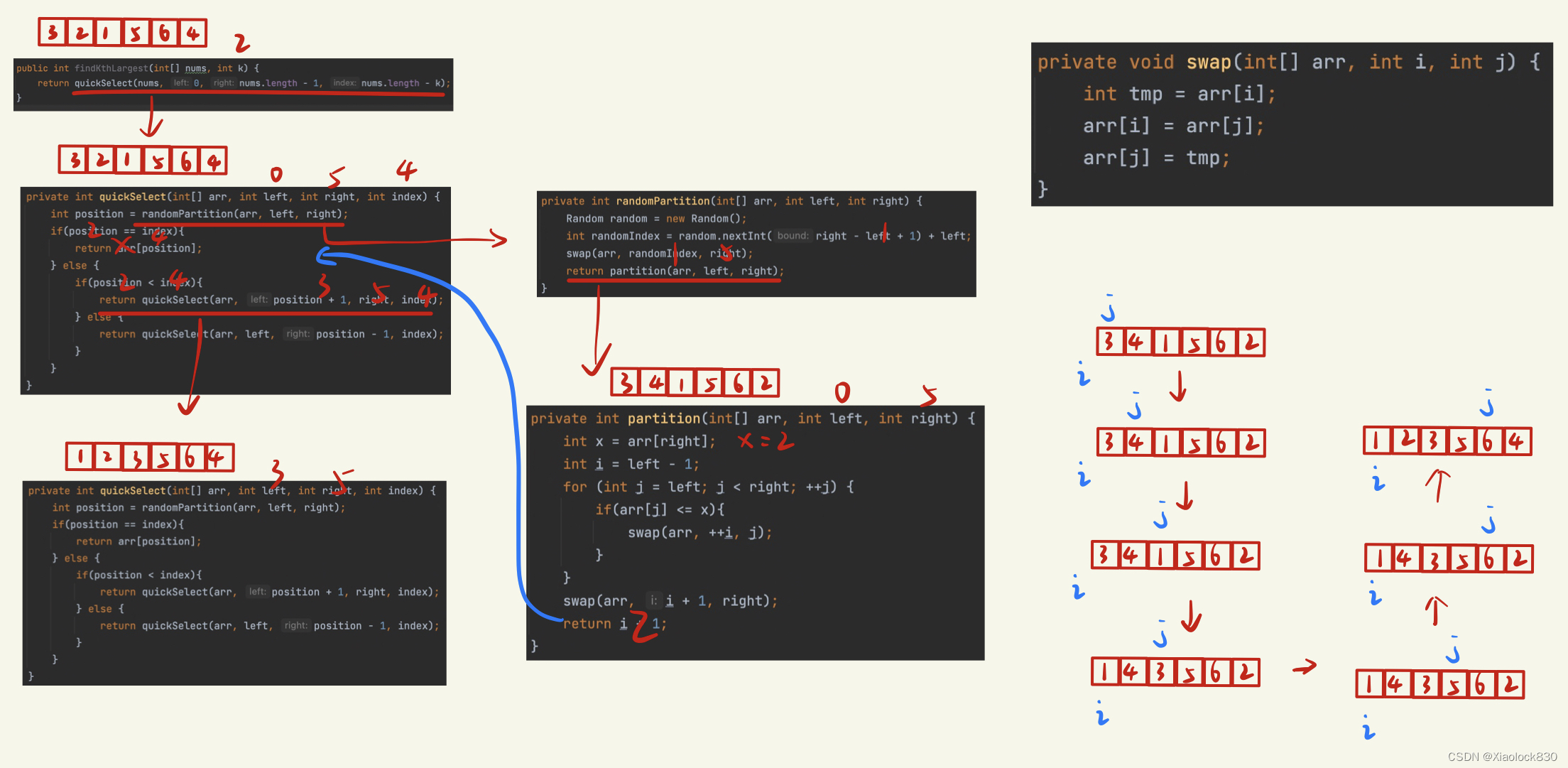
3、跳蚱蜢（2017年省赛，lanqiaoOJ题号642）

【题目描述】

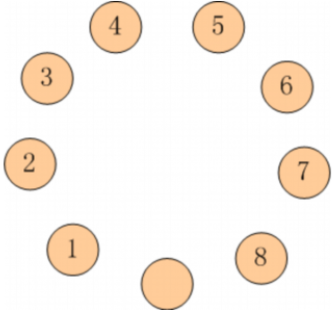
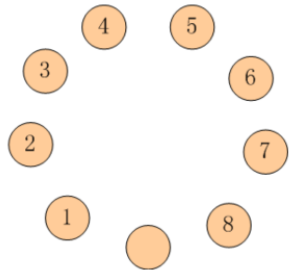
有 9 只盘子，排成 1 个圆圈。其中 8 只盘子内装着 8 只蚱蜢，有一个是空盘。

把这些蚱蜢顺时针编号为1~8。

每只蚱蜢都可以跳到相邻的空盘中，也可以再用点力，越过一个相邻的蚱蜢跳到空盘中。请你计算一下，如果要使得蚱蜢们的队形改为按照逆时针排列，并且保持空盘的位置不变（也就是1-8换位，2-7换位，...），至少要经过多少次跳跃？

从起始状态到终止状态，求最少跳跃次数
最短路径问题
用BFS

直接让蚱蜢跳到空盘有点麻烦，因为有很多蚱蜢在跳。
反过来看，让空盘跳，跳到蚱蜢的位置，简单多了，只有一个空盘在跳。

【画圆为线】

题目是一个圆圈，不好处理，用一个建模技巧 “化圆为线”，把圆形转换为线形。
把空盘看成 0，有 9 个数字 {0,1,2,3,4,5,6,7,8}，一个圆圈上的 9 个数字，拉直成了一条线上的 9 个数字，这条线的首尾两个数字处理成相连的。
八数码问题：有 9 个数字 {0,1,2,3,4,5,6,7,8)，共有 9! = 362880 种排列，不算多。

【最短路径】

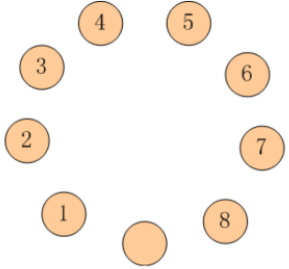
初始状态：“012345678”，目标状态：“087654321”。

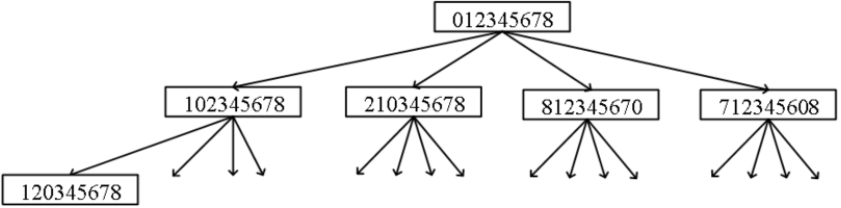
从初始状态 "012345678" 跳一次，有 4 种情况："102345678"、“210345678”、 “812345670”、 “712345608”。然后从这 4 种状态继续跳到下一种状态，一直跳到目标状态为止。

用 BFS 扩展每一层。每一层就是蚱蜢跳了一次，扩展到某一层时发现终点 “087654321”，这一层的深度就是蚱蜢跳跃的次数。

【去重】

如果不去重？
第 1 步到第 2 步，有 4 种跳法；第 2 步到第 3 步，有 4*4 种；...；第 20 步，有 4^20 = 1万亿种。

判重：判断有没有重复跳，如果跳到一个曾经出现过的情况，就不用往下跳了。一共只有 9! =362880 种情况。
代码的复杂度：在每一层，能扩展出最少 4 种、最多 362880 种情况，最后算出的答案是 20 层，那么最多算 20*362880=7,257,600 次。在代码中统计实际的计算次数，是 1451452 次。
队列：最多有 9!=362880 种情况进入队列。

（1）字典去重、用 list 实现队列

速度慢：3s

def insertQueue(q:list,dir:int,news:tuple,vis):     #q是列表，vis是字典，dir是方向
    pos=news[1]         #0的位置
    status=news[0]      #字符串
    insertPos=(pos+dir+9)%9     #新的0的位置
    #将字符串转为列表比较好处理
    t=list(status)      #先转换成列表
    t[pos],t[insertPos]=t[insertPos],t[pos]
    addStatus="".join(t)    #再由列表转换为一个字符串,join完是返回一个字符串
    if addStatus not in vis:
        vis[addStatus]=1    #向字典添加，去重
        q.append((addStatus,insertPos,news[2]+1))

q=[("012345678",0,0)]   #列表，用于实现队列，比较慢
vis={"012345678":1}     #字典，用于去重
while q:
    news=q.pop(0)   #news是一个元组
    if news[0]=="087654321":     #到达了目标状态，输出最少步数
        print(news[2])
        break
    insertQueue(q,-2,news,vis)  #拓展下一层的4种情况
    insertQueue(q,-1,news,vis)
    insertQueue(q,1,news,vis)
    insertQueue(q,2,news,vis)

（2）set() 去重、用 list 实现队列

def insertQueue(q:list,dir:int,news:tuple,vis):     
    pos=news[1]         #0的位置
    status=news[0]      
    insertPos=(pos+dir+9)%9     #新的0的位置
    #将字符串转为列表比较好处理
    t=list(status)      
    t[pos],t[insertPos]=t[insertPos],t[pos]
    addStatus="".join(t)    
    if addStatus not in vis:
        vis.add(addStatus)      #判重 
        q.append((addStatus,insertPos,news[2]+1))

q=[("012345678",0,0)]   
vis=set()
vis.add("012345678")    #判重
while q:
    news=q.pop(0)  
    if news[0]=="087654321":     
        print(news[2])
        break
    insertQueue(q,-2,news,vis) 
    insertQueue(q,-1,news,vis)
    insertQueue(q,1,news,vis)
    insertQueue(q,2,news,vis)

（3）set() 去重、用 deque 实现队列

速度快：1.4s

from collections import *
def insertQueue(q:deque,dir:int,news:tuple,vis:set):     
    pos=news[1]         #0的位置
    status=news[0]      
    insertPos=(pos+dir+9)%9     #新的0的位置
    #将字符串转为列表比较好处理
    t=list(status)      
    t[pos],t[insertPos]=t[insertPos],t[pos]
    addStatus="".join(t)    
    if addStatus not in vis:
        vis.add(addStatus)      
        q.append((addStatus,insertPos,news[2]+1))   #deque的append

q=deque()
q.append(("012345678",0,0))   
vis=set()
vis.add("012345678")    #判重
while q:
    news=q.popleft()  
    if news[0]=="087654321":     
        print(news[2])
        break
    insertQueue(q,-2,news,vis) 
    insertQueue(q,-1,news,vis)
    insertQueue(q,1,news,vis)
    insertQueue(q,2,news,vis)

三、双向广搜

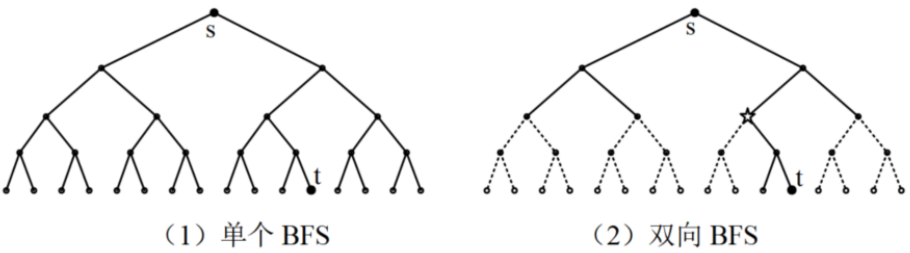
应用场景：有确定的起点 s 和终点 t；把从起点到终点的单向搜索，变换为分别从起点出发和从终点出发的“相遇”问题。
操作：从起点 s（正向搜索）和终点 t（逆向搜索）同时开始搜索，当两个搜索产生相同的一个子状态 v 时就结束，v 是相遇点。得到的 s-v-t 是一条最佳路径。
队列：一般用两个队列分别处理正向 BFS 和逆向 BFS.

【双向广搜的复杂度】

当下一层扩展的状态很多时，双向广搜能大大优化，减少大量搜索

【重新思考上面的例题】

队列 q1：正向搜索
队列 q2：逆向搜索

from queue import *
cnt=0
meet=False
def extend(q,m1,m2):    # m1和m2是字典
    global cnt
    global meet
    s=q.get()
    for i in range(len(s)):
        if s[i]=='0':
            break
    for j in range(4):
        cnt+=1          #统计计算个数
        news=list(s)    #用list比较方便
        if j==0:
            news[(i-2+9)%9],news[i]=news[i],news[(i-2+9)%9]
        if j==1:
            news[(i-1+9)%9],news[i]=news[i],news[(i-1+9)%9]
        if j==2:
            news[(i+1+9)%9],news[i]=news[i],news[(i+1+9)%9]
        if j==3:
            news[(i+2+9)%9],news[i]=news[i],news[(i+2+9)%9]
        a="".join(news) #重新转换成字符串
        if a in m2:
            print(m1[s]+1+m2[a])
            print(cnt)  #打印计算次数
            meet=True
            return
        if a not in m1:
            q.put(a)
            m1[a]=m1[s]+1   #向字典中添加
    meet=False

q1=Queue()
q2=Queue()
q1.put("012345678")
q2.put("087654321")
mp1={'012345678':0}
mp2={'087654321':0}     #定义字典，用于判重
while not q1.empty() and not q2.empty():
    if q1.qsize()<=q2.qsize():
        extend(q1,mp1,mp2)
    else:
        extend(q2,mp2,mp1)
    if meet==True:
        break

由于起点和终点的串不同，正向 BFS 和逆向 BFS 扩展的下一层数量也不同，也就是进入 2 个队列的串的数量不同，先处理较小的队列，可以加快搜索速度。

from queue import *
cnt=0
meet=False
def extend(q,m1,m2):    # m1和m2是字典
    global cnt
    global meet
    s=q.get()
    for i in range(len(s)):
        if s[i]=='0':
            break
    for j in range(4):
        cnt+=1          #统计计算个数
        news=list(s)    #用list比较方便
        if j==0:
            news[(i-2+9)%9],news[i]=news[i],news[(i-2+9)%9]
        if j==1:
            news[(i-1+9)%9],news[i]=news[i],news[(i-1+9)%9]
        if j==2:
            news[(i+1+9)%9],news[i]=news[i],news[(i+1+9)%9]
        if j==3:
            news[(i+2+9)%9],news[i]=news[i],news[(i+2+9)%9]
        a="".join(news) #重新转换成字符串
        if a in m2:
            print(m1[s]+1+m2[a])
            print(cnt)  #打印计算次数
            meet=True
            return
        if a not in m1:
            q.put(a)
            m1[a]=m1[s]+1   #向字典中添加
    meet=False

q1=Queue()
q2=Queue()
q1.put("012345678")
q2.put("087654321")
mp1={'012345678':0}
mp2={'087654321':0}     #定义字典，用于判重
while not q1.empty() and not q2.empty():
    if q1.qsize()<=q2.qsize():
        extend(q1,mp1,mp2)
    else:
        extend(q2,mp2,mp1)
    if meet==True:
        break