题目链接
leetcode在线oj题——数组中第k个最大的元素
题目描述
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
题目示例
输入: [3,2,1,5,6,4], k = 2
输出: 5
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
题目提示
- 1 <= k <= nums.length <= 105
- -104 <= nums[i] <= 104
解题思路
由于我们的题目要求时间复杂度为O(N),因此我们不能使用小根堆来解决这个问题(其时间复杂度为O(NlogN))
可以考虑使用快速排序来解决这个问题,其核心思想是,选定一个基准值,然后遍历整个数组,如果nums[i]比基准值小,那么就将nums[i]移动到基准值的左面,否则就移动到基准值的右边,将所有元素都遍历到后,基准值的位置就是排序好后的位置,我们就可以递归基准值的右侧的所有元素和基准值左侧的所有元素
需要注意的是,由于这道题是让我们找到数组中第k个最大的元素,因此当我们的基准值最后找到的位置是倒数第k个时,这时基准值就是数组中第k个最大的元素
如果我们选择数组中最左侧的元素作为基准值,假设数组十分特殊,本身是从大到小排列的,那么我们每一次递归都需要将基准值移动到最右侧,最终时间复杂度达到了O(N^2),因此我们不能草率的将最左侧或者最右侧的元素定义为基准值。在这里采用将最右侧元素和数组中随机一个元素互换位置后,再将最右侧元素作为基准值
详细代码
class Solution {
public int findKthLargest(int[] nums, int k) {
return quickSelect(nums, 0, nums.length - 1, nums.length - k);
}
private int quickSelect(int[] arr, int left, int right, int index) {
int position = randomPartition(arr, left, right);
if(position == index){
return arr[position];
} else {
if(position < index){
return quickSelect(arr, position + 1, right, index);
} else {
return quickSelect(arr, left, position - 1, index);
}
}
}
private int randomPartition(int[] arr, int left, int right) {
Random random = new Random();
int randomIndex = random.nextInt(right - left + 1) + left;
swap(arr, randomIndex, right);
return partition(arr, left, right);
}
private int partition(int[] arr, int left, int right) {
int x = arr[right];
int i = left - 1;
for (int j = left; j < right; ++j) {
if(arr[j] <= x){
swap(arr, ++i, j);
}
}
swap(arr, i + 1, right);
return i + 1;
}
private void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
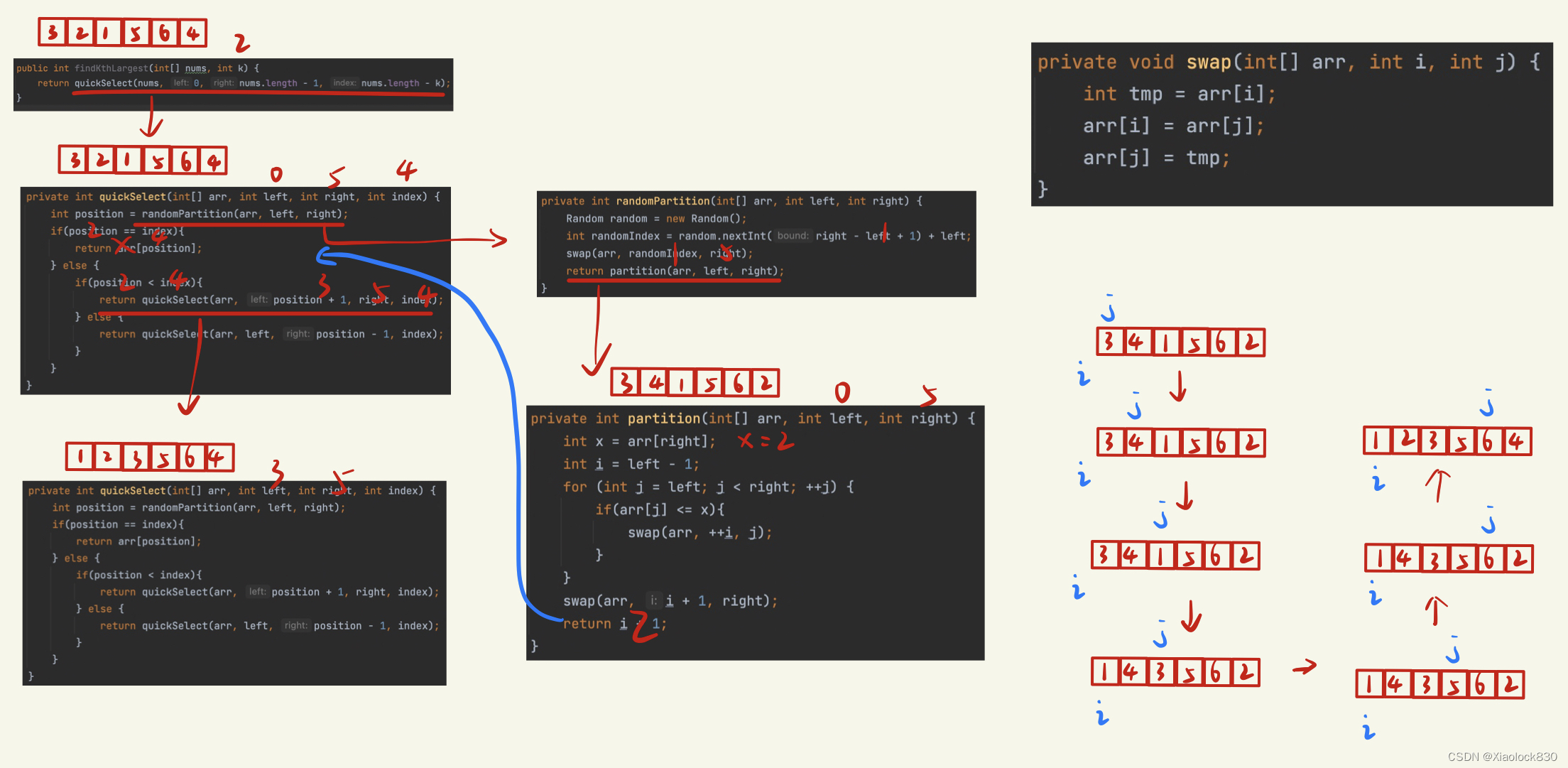
代码执行流程图
可以对照上面的代码来看一下流程图,这里选择的随机位置是1,对应的基准值为2