目录​​​​​​​

77. 组合：

问题描述：

实现代码与解析：

递归（回溯）：

原理思路：

剪枝优化版：

原理思路：

216. 组合总和 III：

问题描述：

实现代码与解析：

回溯：

原理思路：

剪枝版：

---

77. 组合：

问题描述：

        给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

实现代码与解析：

递归（回溯）：

class Solution {
public:
    vector<int> path;//记录路径
    vector<vector<int>> result;//记录结果
    void backtrack(int n,int k,int start)
    {
        //终止条件
        if(path.size()==k)
        {
            result.push_back(path);
            return;
        }
        for(int i=start;i<n+1;i++)
        {
            path.push_back(i);
            backtrack(n,k,i+1);//递归
            path.pop_back();//回溯
        }
    }
    vector<vector<int>> combine(int n, int k) 
    {
       backtrack(n,k,1);
       return result;  
    }
};

原理思路：

        回溯的经典题，在遇到循环次数不确定的问题时，通常都是用递归回溯来解决，而递归的终止条件便就是循环结束的条件，通常也就是我们获取结果的时候。

       首先确定终止条件，显然就是路径path已经搜集了k个值，我们就将其放入result中，这里还是很好理解的。

        然后我们就开始循环，毕竟我们要解决的就是这种嵌套循环问题，循环里我们将当前值录入path，递归下一层，最重要的是下面的回溯。

path.pop_back();//回溯

        简单理解，就拿例一举例（n=4，k=2），我们取完【1，2】这个结果，就该取【1，3】了，若这时2不弹出path，显然是取不到【1，3】和其他结果的。其实这里和二叉树的某些题思路一样，只不过二叉树我们要搜集结果可能就把path路径放入参数中了，而参数是值传递，在递归返回时，自动就弹出了，而这里我们用的全局变量，需要我们手动弹出。

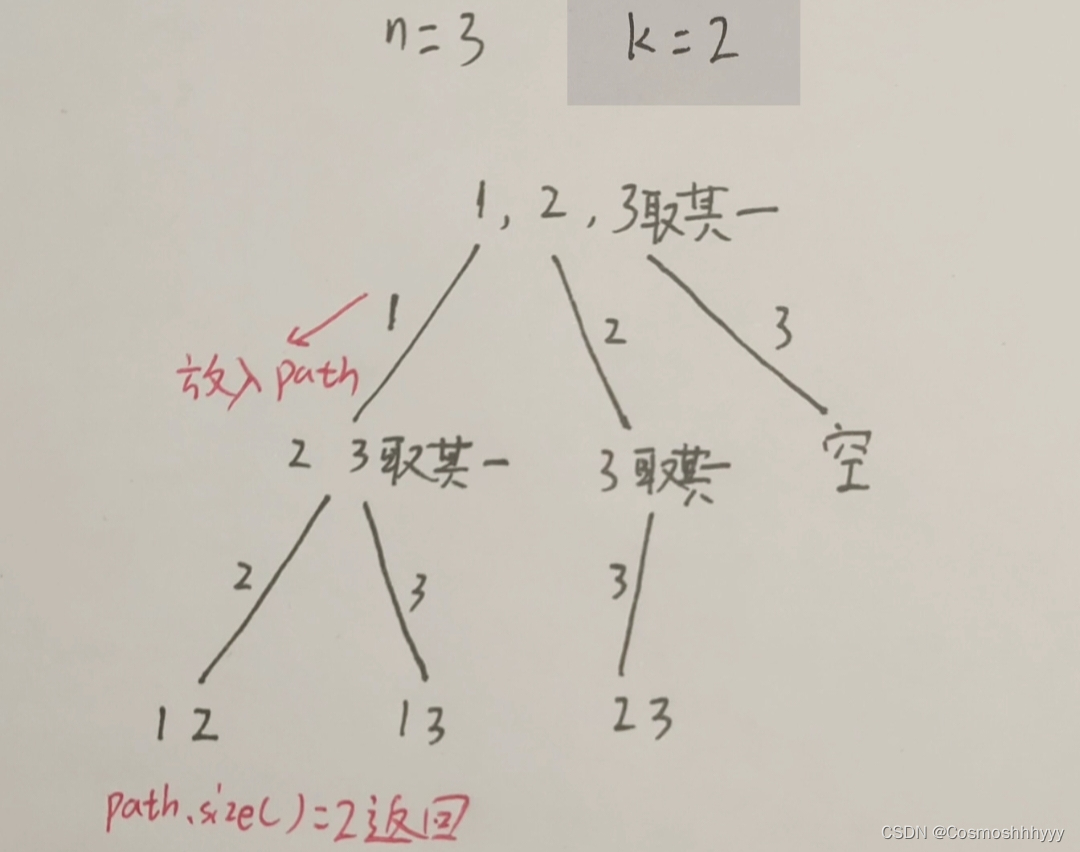
        方便大家进一步理解，我们可以想象为一颗树，叶子结点的值就为路径，如下图：

剪枝优化版：

class Solution {
public:
    vector<int> path;//记录路径
    vector<vector<int>> result;//记录结果
    void backtrack(int n,int k,int start)
    {
        //终止条件
        if(path.size()==k)
        {
            result.push_back(path);
            return;
        }
        for(int i=start;i<=n-(k-path.size())+1;i++)
        {
            path.push_back(i);
            backtrack(n,k,i+1);//递归
            path.pop_back();//回溯
        }
    }
    vector<vector<int>> combine(int n, int k) 
    {
       backtrack(n,k,1);
       return result;  
    }
};

原理思路：

        其实就改了一处而已，就是循环条件。

for(int i=start;i<=n-(k-path.size())+1;i++)

        在实际循环的时候我们会发现，其实有的循环最后是不会得到结果的无效循环，例如n=3，k=3的时候，显然只有一个结果【1，2，3】，我们第一层循环显然只用取1就可以了，后面循环2，3的时候显然是不可能再有结果了，第一层2，3的循环就是无效的，当然实际情况会复杂一定，剪枝也可以发生在第二层或则其他层里，这就是剪枝的原理，其实还是很简单的。

216. 组合总和 III：

问题描述：

        找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

• 只使用数字1到9
• 每个数字 最多使用一次 

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

实现代码与解析：

回溯：

class Solution {
public:
    vector<int> path;//记录路径
    int pathSum=0;//记录路径和
    vector<vector<int>> result;
    void backstack(int n,int k,int startIndex)
    {
        //符合返回条件
        if(path.size()==k)
        {
            //返回记录条件
            if(pathSum==n)
            {
                result.push_back(path);
            }
            return;
        }      
        for(int i=startIndex;i<=9;i++)
        {
            path.push_back(i);
            pathSum+=i;
            backstack(n,k,i+1);
            path.pop_back();//回溯
            pathSum-=i;//回溯
        }
        return;
    }
    vector<vector<int>> combinationSum3(int k, int n) 
    {
        backstack(n,k,1);
        return result;
    }
};

原理思路：

        与上面一题思路完全一致，就多了个判断和，过于简单就不再解释了。

        这里同样给出剪枝版的代码。

剪枝版：

class Solution {
public:
    vector<int> path;//记录路径
    int pathSum=0;//记录路径和
    vector<vector<int>> result;
    void backstack(int n,int k,int startIndex)
    {
        //符合返回条件
        if(path.size()==k)
        {
            //返回记录条件
            if(pathSum==n)
            {
                result.push_back(path);
            }
            return;
        }      
        for(int i=startIndex;i<=9-(k-path.size())+1;i++)//剪枝
        {
            path.push_back(i);
            pathSum+=i;
            backstack(n,k,i+1);
            path.pop_back();//回溯
            pathSum-=i;//回溯
        }
        return;
    }
    vector<vector<int>> combinationSum3(int k, int n) 
    {
        backstack(n,k,1);
        return result;
    }
};