python3 tuple类型的使用

1. 基本知识

a. 元组（tuple）与列表类似, 不同之处在于元组的元素(项)不能修改。
b. 元组写在小括号 () 里，元素之间用逗号隔开。
c. 元组中的元素类型也可以不相同。
d. 构造包含0个或1个元素的元组比较特殊, 所以有一些额外的语法规则：
  tuple1= () # 空元组
  tuple2= (20, ) # 一个元素, 需要在元素后面加逗号, 逗号至关重要, 必须要写
e. tuple()函数：它将一个序列作为参数，并将其转换为元组。如果参数已经是元组，就原封不动地返回它。

t1 = (1,2,3)
t2 = (4,5,6)

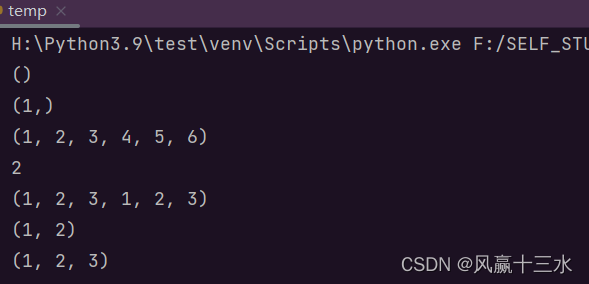
print(())       # 空元组
print((1,))     # 含有一个元素的元组
print(t1+t2)    # 相加
print(t1[1])    # 索引获取项
print(t1*2)     # 相乘
print(t1[0:2])  # 截取
print(t1[:])    # 截取

---

tuple()函数：

print(tuple("HelloWorld"))
print(tuple([1,2,3]))
print(tuple((1,2,3)))

---

成员资格运算符：

print(1 in tuple([1,2,3]))

2. 删除元组

元组中的元素值是不允许删除的，但我们可以使用del语句来删除整个元组。
(1) 单独删除元组项，报错

t = (1,2,3,4,5,6)
del t[1]

(2) 删除整个元组

t = (1,2,3,4,5,6)
del t

3. 脚本操作符

print(len((1,2,3,4,5,6)))   # 元素个数
print((1,1,2)+(2,3,4))      # 连接
print((1,2)*3)              # 复制
print(11 in (1,2,3))        # 成员运算符
for num in (1,2,3,4):       # 迭代
    print(num)

4. 元组不可变

（1）元组的项是不能够改变的，否则报错。

t = (1,2,3,4)

t[0] = 111

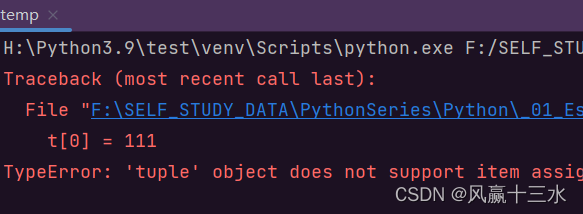
（2）内存改变

t = (1,2,3,4)
print(id(t))
t = (1)
print(id(t))

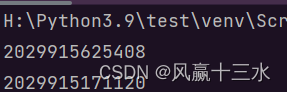
可以很清晰的看到，两次t的内存是不一样的。
从以上实例可以看出，重新赋值的元组t，绑定到新的对象了，不是修改了原来的对象。

5. 内置函数

len(tuple)：计算元组元素个数。
max(tuple)：返回元组中元素最大值。
min(tuple)：返回元组中元素最小值。
tuple(iterable)：将可迭代系列转换为元组。

t = (1,2,35,6,7,8)

print(len(t))
print(max(t))
print(min(t))
print(tuple([1,2,3,4]))