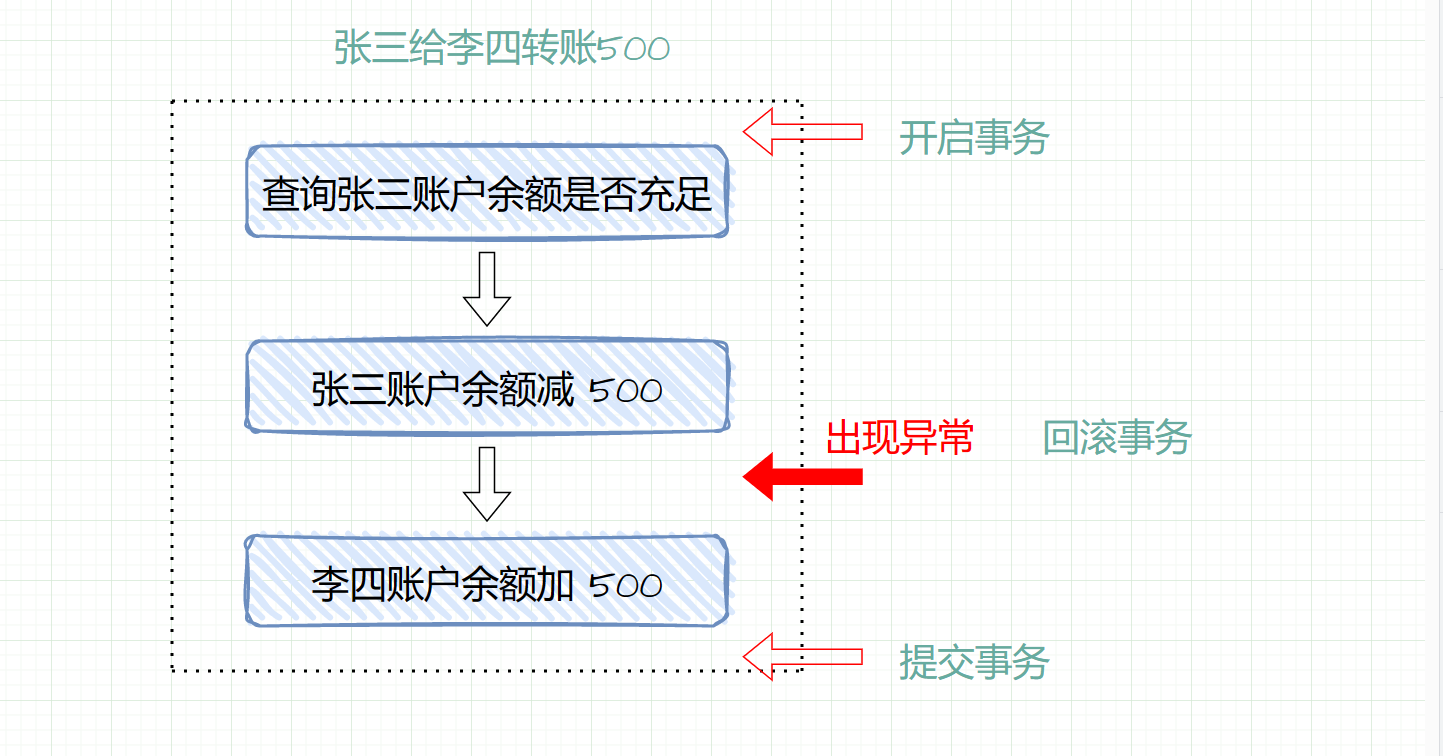
1. chmod 语法

chmod为修改文件/文件夹权限，有以下两种操作，其中-R表示递归修改

• chmod {ugoa} {+-=} {rwx} [文件或目录] -R
• chmod [mode=421] [文件或目录] -R

2. chmod {ugoa} {+-=} {rwx} [文件或目录] -R

• u：文件或目录的所有者，g：所属组，o：其它用户，a：所有用户(all users)
• +-= : 可以通过该操作分别给 {ugoa} 增加 / 减少 / 赋值 {rwx}权限
• r：可读，w：可写，x：可执行权限
• 若想一次性执行多条操作，可用逗号分割，如 【chmod u+x, g-w 文件名】

见下面示例：

初始化，只包含一个hello.txt文件，且权限为：-rw-rw-r--

liu@SLR:/hd1/Dling/lane/Wmq/test$ ls -l
total 8
-rw-rw-r-- 1 liu liu 4290 1月  19 22:21 hello.txt

执行 chmod u+x hello.txt，为所有者增加可执行权限，权限更新为：-rwxrw-r--

liu@SLR:/hd1/Dling/lane/Wmq/test$ chmod u+x hello.txt
liu@SLR:/hd1/Dling/lane/Wmq/test$ ls -l
total 8
-rwxrw-r-- 1 liu liu 4290 1月  19 22:21 hello.txt

3. chmod [mode=421] [文件或目录] -R

最常用的是这种方式。其中421分别代表 r, w, x， rwx=4+2+1=7，rw- = 4+2+0=6。因此 rwxrw-r-- 的数字表示就是764

当前目录结构为，一个文件dir1包含两个子文件

| --------dir1

|------------------t1.txt

|------------------t2.txt

 通过下图可知，dir1的权限为 rwxrwxr-x，两个txt文件的权限为 rw-rw-r--

liu@SLR:/hd1/Dling/lane/Wmq/test$ ls -l
total 4
drwxrwxr-x 2 liu liu 4096 1月  20 12:52 dir1

liu@SLR:/hd1/Dling/lane/Wmq/test$ cd dir1/
liu@SLR:/hd1/Dling/lane/Wmq/test/dir1$ ls -l
total 0
-rw-rw-r-- 1 liu liu 0 1月  20 12:52 t1.txt
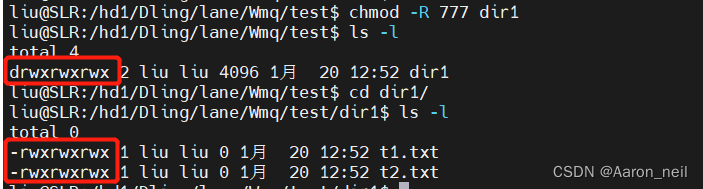
-rw-rw-r-- 1 liu liu 0 1月  20 12:52 t2.txt

递归更改dir文件极其子文件的权限均为 rwx，用 chmod -R 777 dir1，可看到权限均发生了变化

4. 注意事项！！

文件和文件夹对于 rwx 权限的定义和范围是不同的，如下

	权限定义	对于文件	对于文件夹
r	读权限	可以查看文件内容	可以列出目录中的内容
w	写权限	可以修改文件内容	可以在目录中创建、删除文件
x	执行权限	可以执行文件	可以进入目录

对于一个目录的的w权限表示可以在目录中创建、删除文件。因此能够删除目录下某一文件的前提并不是对该文件有写权限，因为对该文件的写权限只是可以修改文件内容，如果能够删除该文件则是对该文件所在目录有写权限，而不是对该文件有写权限。如果我想看一个文件内容，前提就是能够进入该文件所在的文件夹目录，也就是能够对文件夹有x权限。如果一个文件夹什么权限都没有，那么该文件夹下任意文件的权限也没有任何意义。