链式法则

简单的说链式法则就是原本y对x求偏导，但是由于过程较为复杂，我们需要将函数进行拆分，通过链式进行分别求导，这样会使整个计算更为简单。

假设f = k ( a + b c ) f = k(a + bc)f=k(a+bc)

通俗来说，链式法则表明，知道z相对于y的瞬时变化率和y相对于x的瞬时变化率，就可以计算z相对于x的瞬时变化率作为这两个变化率的乘积。其实就是求复合函数导数的过程。
在这里插入图片描述
用链式法则（将这些梯度表达式链接起来相乘。）分别对变量a、b、c进行求导：

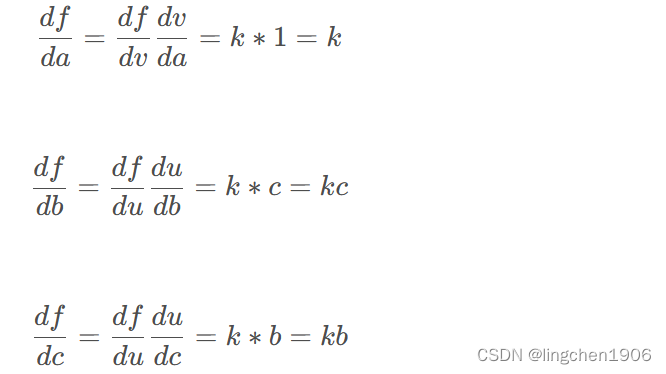
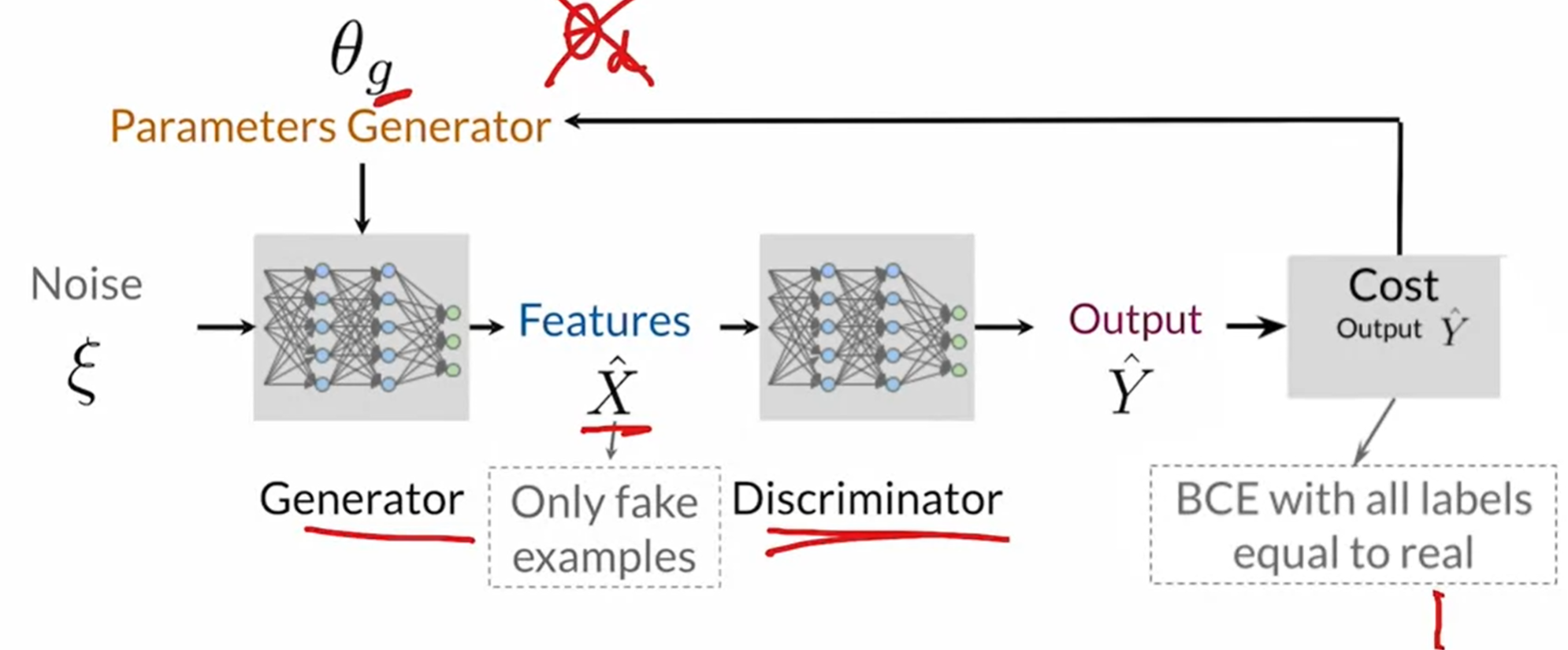
前向传播

前向传播（forward propagation或forward pass）指的是：按顺序（从输入层到输出层）计算和存储神经网络中每层的结果。

对于中间变量：
在这里插入图片描述
W为参数权重，b为函数偏置，函数结果经过激活函数C（常见的激活函数有Sigmoid、tanh、ReLU）

假设损失函数为l，真实值为h，我们可以计算单个数据样本的损失项，

在不考虑优化函数，单个神经元从输入到输出结束，后面需要对误差进行反向传播，更新权值，重新计算输出。

反向传播

反向传播（backward propagation或backpropagation）指的是计算神经网络参数梯度的方法。简言之，该方法根据微积分中的链式规则，按相反的顺序从输出层到输入层遍历网络。该算法存储了计算某些参数梯度时所需的任何中间变量（偏导数）。

（1）梯度下降
在说反向传播算法前，先简单了解一些梯度下降，对于损失函数(这里假设损失是MSE，即均方误差损失)
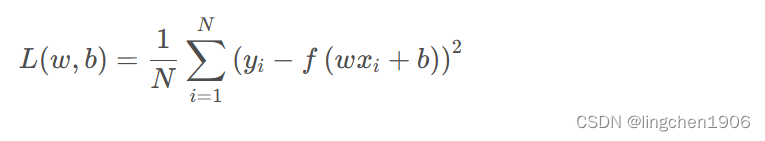
在这里插入图片描述

除此以外还有一些再次基础上优化的其他梯度下降方法：小批量样本梯度下降（Mini Batch GD)、随机梯度下降（Stochastic GD)等。
（2）反向传播
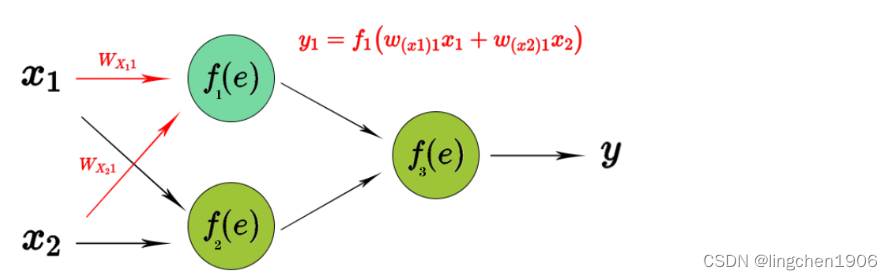
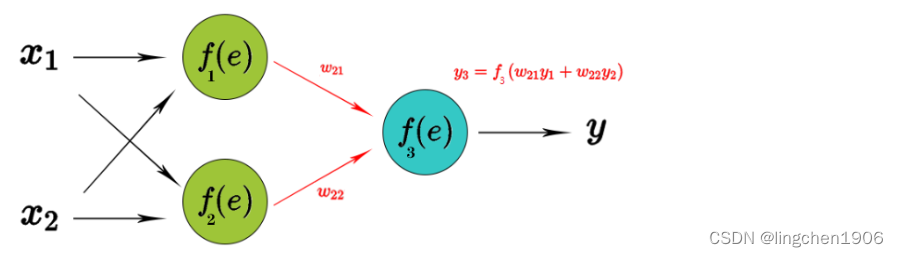
反向传播计算损失函数相对于单个输入-输出示例的网络权重的梯度，为了说明这个过程，使用了具有2个输入和1个输出的2层神经网络，如下图所示：
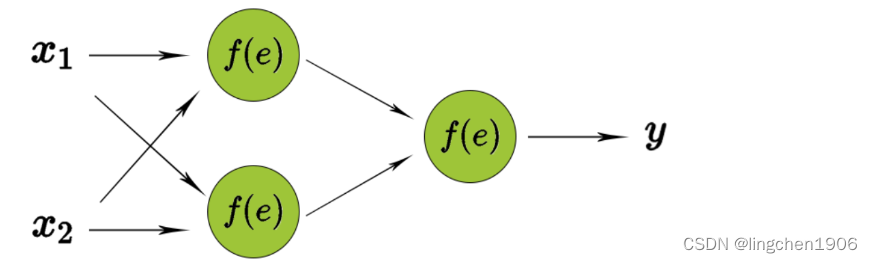
在这里插入图片描述
不考虑优化算法，单个神经结构如下图所示，第一个单元将权重系数和输入信号的乘积相加。第二单元为神经元激活函数（反向传播需要在网络设计时激活函数可微的），如下图所示：

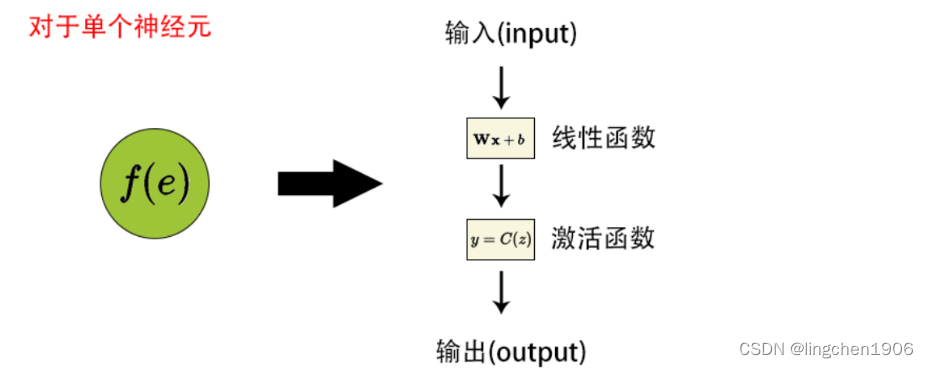
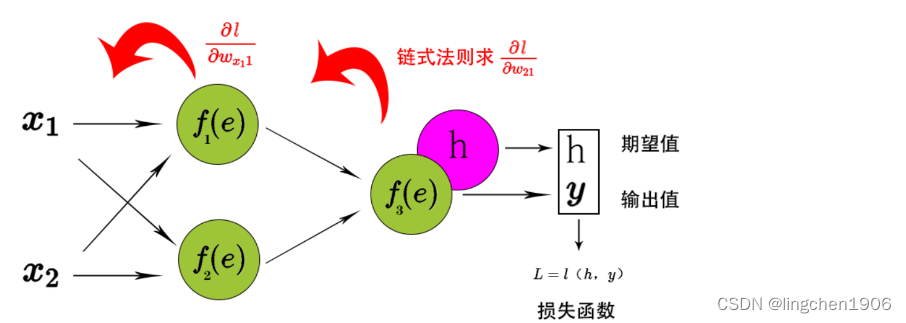
根据链式法则求出所有的更新后的权重W WW梯度，偏值使用同样的方法。通过反向传播，计算损失函数与当前神经元权重的最陡下降方向。然后，可以沿最陡下降方向修改权重，并以有效的方式降低损失。
（3）反向传播代码

def optimize(w, b, X, Y, num_iterations, learning_rate):
    costs = []

    for i in range(num_iterations):

        # 梯度更新计算函数
        grads, cost = propagate(w, b, X, Y)

        # 取出两个部分参数的梯度
        dw = grads['dw']
        db = grads['db']

        # 按照梯度下降公式去计算
        w = w - learning_rate * dw
        b = b - learning_rate * db

        if i % 100 == 0:
            costs.append(cost)
        if i % 100 == 0:
            print("损失结果 %i: %f" % (i, cost))
            print(b)
    params = {"w": w,
              "b": b}
              
    grads = {"dw": dw,
             "db": db}
    return params, grads, costs

def propagate(w, b, X, Y):
    m = X.shape[1]

    # 前向传播
    A = basic_sigmoid(np.dot(w.T, X) + b)
    cost = -1 / m * np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))

    # 反向传播
    dz = A - Y
    dw = 1 / m * np.dot(X, dz.T)
    db = 1 / m * np.sum(dz)

    grads = {"dw": dw,
             "db": db}

    return grads, cost