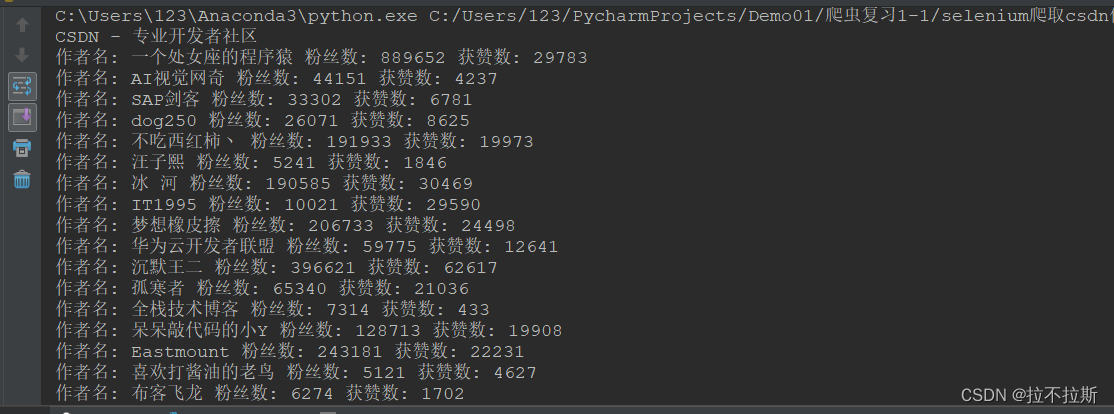
一 卡方分布

定义

设$X_1,X_2,...,X_n$ 独立同分布于标准正态分布N(0, 1), 则${\chi }^2=X_1^2+...+X_n^2$的分布称为 自由度为 n 的${\chi }^2$分布， 记为${\chi }^2$ ~ ${\chi }^2(n)$

${\chi }^2$ 分布又称为卡方分布。
卡方分布的期望 E(${\chi }^2$) = n, 方差D(${\chi }^2$) = 2n.

就是说来自于独立的标准正态分布的随机变量的平方和 叫做 卡方分布。

二 F分布

定义

设$X_1$ ~ ${\chi }^2$(m), $X_2$ ~ ${\chi }^2$(n), $X_1$ 与$X_2$独立， 则称
$F=\frac{\frac{X_1}{m}}{\frac{X_2}{n}}$ 的分布是自由度为m与n 的F分布， 记为F ~ F(m, n). 其中m称为分子自由度， n称为分母自由度。

三 t分布

定义

设$X_1$与$X_2$独立， 且$X_1$~N(0, 1), $X_2$~${\chi }^2(n)$, 则称 $t=\frac{X_1}{\sqrt{\frac{X_2}{n}}}$ 的分布为自由度为n的 t 分布, 记为 t ~ t(n)

四 三大抽样分布

三大抽样分布

五 光说不练假把式， 看例题

题1
设总体 X~N(0, ${\sigma }^2$), $X_1,X_2,$ … $X_n$ 为来自X的样本， $\overline{x}$ 为样本均值， $s^2$为样本方差， 则 $\frac{\overline{x}}{x/\sqrt{n}}$ ~ __________.

解: 因为X服从正态分布， 所以

$\frac{\overline{x}-\mu }{s/\sqrt{n}}=\frac{\overline{x}}{s/\sqrt{n}}$ ~ $t(n-1)$