先简单了解一下树的概念,从而进一步了解二叉树,最后进行代码测试。
树概念及结构(了解)
在认识而二叉树之前我们首先了解一下树的概念。
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它
叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
我们与之前学过的 顺序表、单链表、双链表、栈和队列,都是线性结构,及必须访问了前一个或者后一个才能访问目标节点,而我们今天了解的数据结构(树)是非线性结构,可以跳过部分节点直接访问目标节点。
树:顾名思义长得像现实生活的树(倒着的)。

数据结构(树)
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
注意:我们如果把A看成’1‘层的话,那么‘ 0 ’层表示没有树;如果把A用数组的下标表示的化就是’0‘,哪儿买没有树就是’-1‘(这个表达有点怪)。
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B
的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节
点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
这里其实我们可以用我们现实生活中的复杂的亲戚关系作类比。
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的多颗树的集合称为森林;(数据结构中的学习并查集本质就是
一个森林)
树的表示
我们发现如果我们把它设置成一个静态的,就不能够实现。
我们假设树有许多孩子。那么我们可以尝试把代码写成这样:
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _firstChild2; // 第二个孩子结点
struct Node* _firstChild3; // 第三个孩子结点
//...
DataType _data;
};
我们发现这样是不行的。这里其实我们如过运用c++里的知识,可以想象一下,我们如果可以自由的开辟空间,那么有再多的‘孩子’其实也无所谓。
struct TreeNode
{
int data;
vector<struct TreeNode*> childs;
};但是我们的目的是打算用C语言实现,我们能不能用“左孩子右兄弟”的方式来解决呢?
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};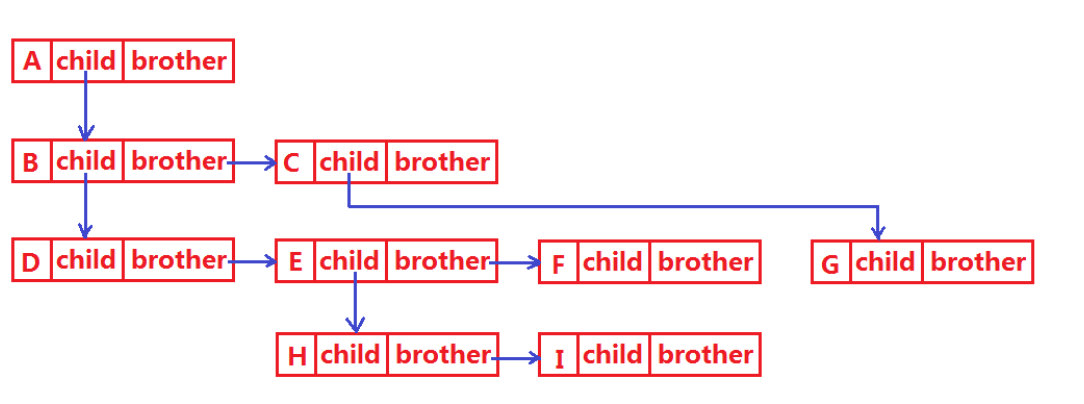
“左孩子右兄弟”的实现原理
其实通过存“父亲的下标”也能够实现。(其实并查集就是用的方法,一般树不用该方法)

树的应用
我们常用的文件夹结构就是这样:
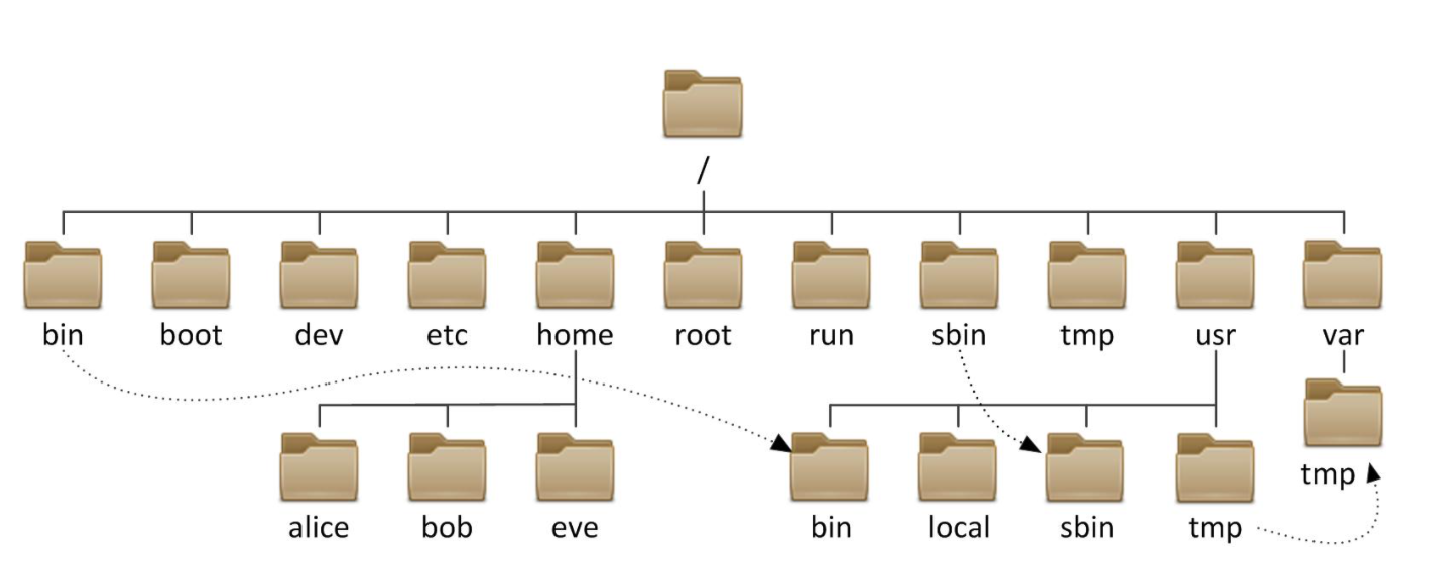
文件夹(Linux)
二叉树的组成部分
根节点
左子树
右子树
分 治 算 法 : 分 而 治 之 , 大 问 题 分 成 类 似 子 问 题 , 子 问 题 再 分 成 子 问 题 .
直 到 子 问 题 不 可 再 分 割
我们对数的概念有所了解以后再来了解二叉树。
二叉树
前序顺序
原理:根节点,左子树和右子树。

顺序:A B D NULL NULL NULL C E NULL NULL F NULL NULL
这里有个窍门,就是把一侧全部数完,再来数另一侧的,跟递归一样。
中序顺序
原理:左子树,根节点和右子树。
一样的图。依照我们之前学的套路。
顺序就是:NULL D NULL B NULL A NULL E NULL C NULL F NULL
那么知道后序顺序的原理——左子树,右子树和根节点。我们写出后序顺序应该不难,大家可以自己尝试一下,有问题欢迎大家评论区讨论。
测试
我们讲了这么多。我们用代码简单实现一下前序顺序。
按照我们之前讲的套路,初始化就是这样。
typedef char BTDateType;
typedef struct BinaryTree
{
struct BinaryTree* left;
struct BinaryTree* right;
BTDateType data;
}BTDnode;那么访问就是这样实现。
//访问
void PreOrder(BTDnode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%c ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}当然如果大家想实现中序的话就是这样的。
//访问
void PreOrder(BTDnode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PreOrder(root->right);
//中序就是先走左边
printf("%c ", root->data);
PreOrder(root->left);
}这里其实我们可以用我们之前学的单链表直接调用,但是这样有点繁琐,我们完全可以自己做一个静态简易版链表。
int main()
{
//链表
BTDnode* A = (BTDnode*)malloc(sizeof(BTDnode));
A->data = 'A';
A->left = NULL;
A->right= NULL;
BTDnode* B = (BTDnode*)malloc(sizeof(BTDnode));
B->data = 'B';
B->left = NULL;
B->right = NULL;
BTDnode* C = (BTDnode*)malloc(sizeof(BTDnode));
C->data = 'C';
C->left = NULL;
C->right = NULL;
BTDnode* D = (BTDnode*)malloc(sizeof(BTDnode));
D->data = 'D';
D->left = NULL;
D->right = NULL;
BTDnode* E= (BTDnode*)malloc(sizeof(BTDnode));
E->data = 'E';
E->left = NULL;
E->right = NULL;
return 0;
}然后我们再来链接在一块就是了。
int main()
{
BTDnode* A = (BTDnode*)malloc(sizeof(BTDnode));
A->data = 'A';
A->left = NULL;
A->right= NULL;
BTDnode* B = (BTDnode*)malloc(sizeof(BTDnode));
B->data = 'B';
B->left = NULL;
B->right = NULL;
BTDnode* C = (BTDnode*)malloc(sizeof(BTDnode));
C->data = 'C';
C->left = NULL;
C->right = NULL;
BTDnode* D = (BTDnode*)malloc(sizeof(BTDnode));
D->data = 'D';
D->left = NULL;
D->right = NULL;
BTDnode* E= (BTDnode*)malloc(sizeof(BTDnode));
E->data = 'E';
E->left = NULL;
E->right = NULL;
A->left = B;
A->right = C;
B->left = D;
B->right = E;
PreOrder(A);
printf("\n");
return 0;
}但是有些同学递归学的有点迷糊,就难以理解是如何实现的。这里我再来画一幅图。

我们接下来再来画一下递归图。
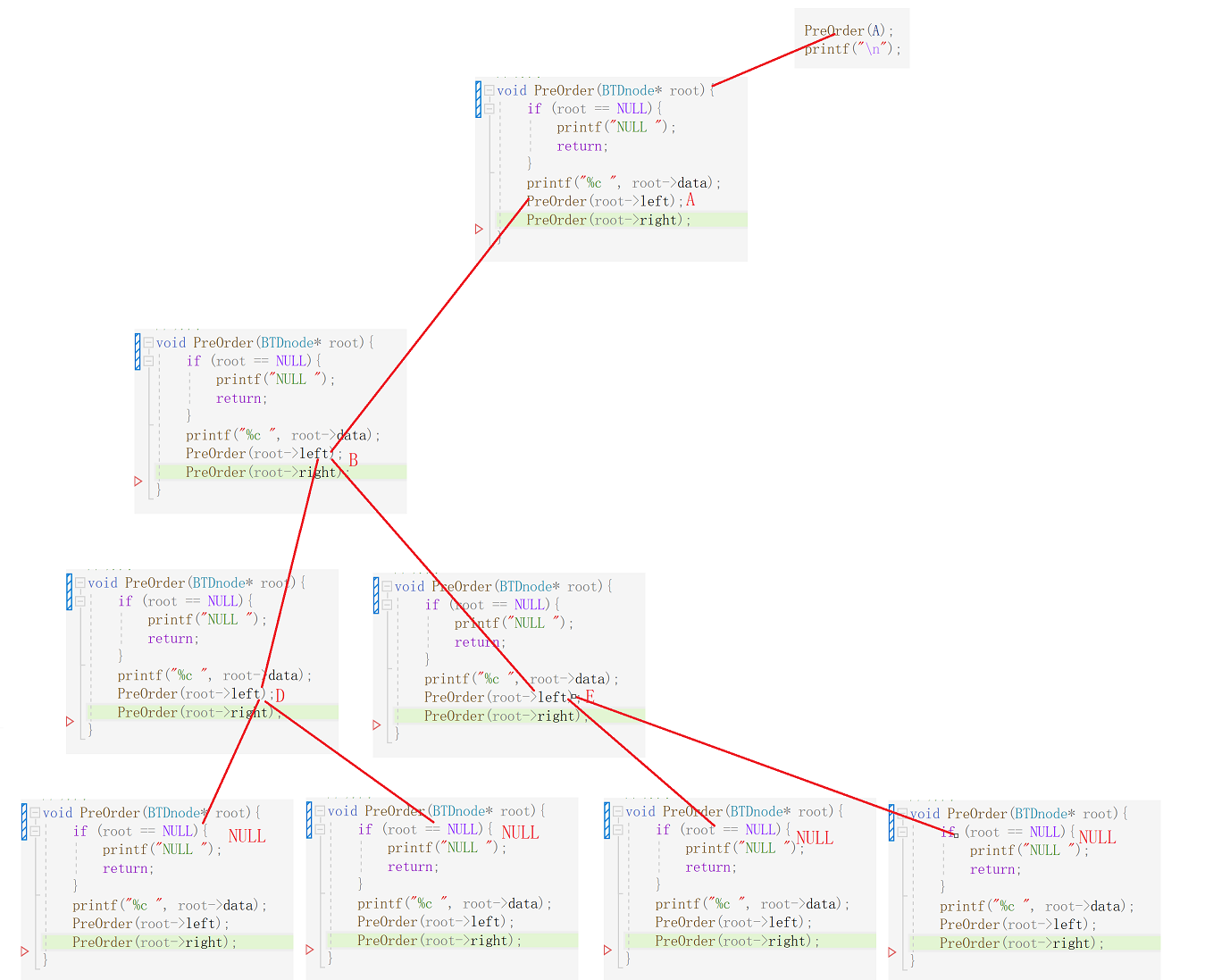
递归原理(左图)
其实画完比较复杂的左图,相对简单的右图完全可以想象出来,各位小伙伴可以自己动手试一下。
总结
我们一起探讨了,数的结构和概念,从而引出本节重点——二叉树,简单了解完其概念和原理以后,我们就对其做了测试,为了进一步理解二叉树的原理,我再用递归的方式对二叉树做了原理图,我们发现递归的原理图和二叉树长得很像。
下一节我们将进一步学习二叉树的原理。
欢迎大家的评论和点赞!