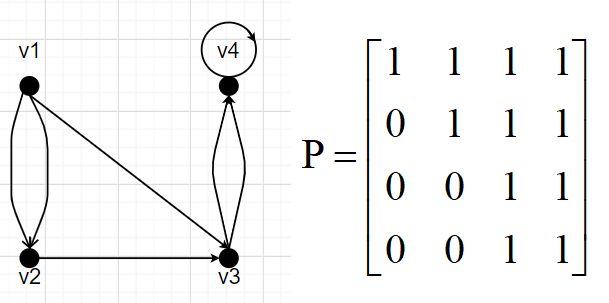
图的基本概念

1 图

1.1 图的定义

定义1： 一个无向图G是一个有序的二元组<V,E>，其中
（1）V是一个非空有穷集，称为顶点集，其元素称为顶点或结点。
（2）E是无序积V&V的有穷多重子集，称为边集，其元素称为无向边，简称边。

定义2： 一个有向图D是一个有序的二元组<V,E>，其中
（1）V是一个非空有穷集，称为顶点集，其元素称为顶点或结点。
（2）E是笛卡尔积VXV的有穷多重子集，称为边集，其元素称为有向边，简称边。

在图G中,

• 如果每条边都是有向边, 该图称为有向图(Directed Graph)
• 若每条边都是无向边, 该图G称为无向图(Undirected Graph)
• 如果有些边是有向边, 另一些边是无向边, 图G称为混合图(Mixed Graph)

定义3：
（1）无向图和有向图统称为图，但有时把无向图简称为图，统常用G表示无向图，D表示有向图。
（2）顶点数称作图的阶，n个顶点的图称为n阶图。
（3）一条边也没有的图称为零图，n阶零图记作$N_n$,一阶零图$N_1$称为平凡图(平凡图只有一个顶点，没有边)。
（4）将有向图的各条有向边改成无向边后所得到的无向图称为这个有向图的基图。
（5）设G=<V,E>为无向图，$e_k=(v_i,v_j)$∈E，称$v_i,v_j$为$e_k$的端点，$e_k$与$v_i,v_j$关联。

• 若$v_i\ne v_j$,则称$e_k$与$v_i,v_j$的关联次数是1。
• 若$v_i=v_j$,则称$e_k$与$v_i,v_j$的关联次数是2，并称$e_k$为环。
• 如果顶点$v_i,v_j$不与边$e_k$关联，则称$e_k$与$v_i,v_j$的关联次数是0。
• 若两个顶点$v_i与v_j$之间有一条边连接，则称这两个顶点相邻，若两条边至少有一个公共端点，则称这两条边相邻。

（6）图(无向的或有向的)中没有边关联的顶点称为孤立点。
（7）在无向图中，如果关联一对顶点的无向边多于一条，则称这些边为平行边，平行边的条数称为重数。（平行边的条数是n-1）在有向图中，如果关联一对顶点的有向边多于1条，并且这些边的始点终点相同(它们的方向相同)，则称这些边为平行边，含平行边的图称为多重图，即不含平行边也不含环的图称为简单图。

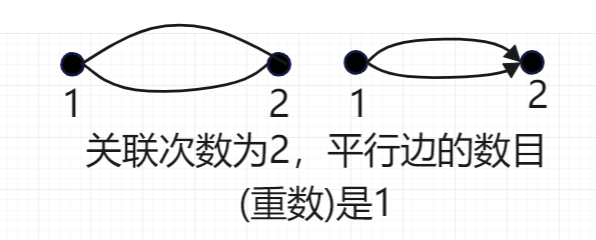
（8）设G=<V,E>为无向图，$\forall v$∈V，称$v$作为边的端点的次数为$v$的度数，简称度，记作$d(v)$。设D=<V,E>为有向图，$\forall v$∈V，称$v$作为边的始点的次数为$v$的出度，记作$d^{+}(v)$,称$v$作为边的终点的次数为$v$的入度，记作$d^{-}(v)$，称$d^{+}(v)$+$d^{-}(v)$为$v$的度数，记作$d(v)$。

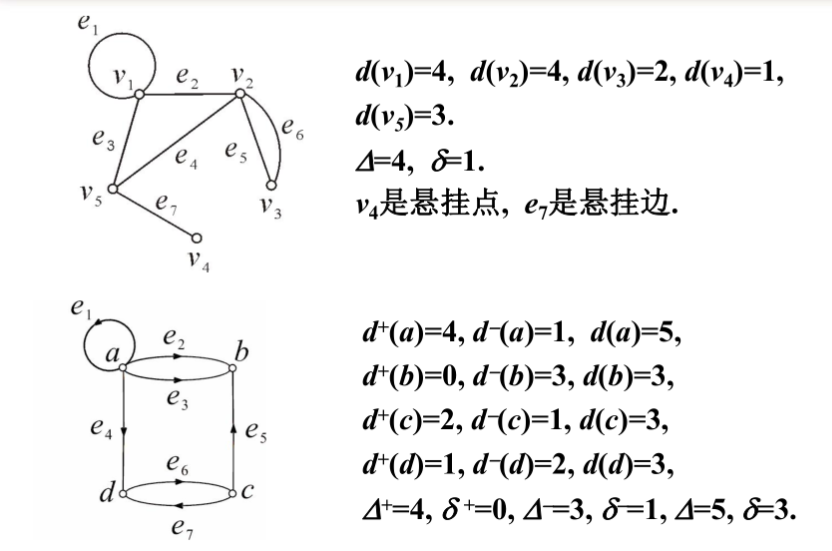
1.2 握手定理

定理1：在任何无向图中，所有顶点的度数之和等于边数的2倍。
     在任何有向图中，所有顶点的度数之和等于边数的2倍；所有顶点的入度之和等于所有顶点的出度之和，都等于边数。

$\sum _{v\in V}d(v)=2m,（其中d(v)是度数之和，m是边数）$

定理2：任何图中(无向图或有向图)中，奇度顶点的个数是偶数（要满足握手定律，偶数个奇度顶点的和为偶数，满足2倍关系）。
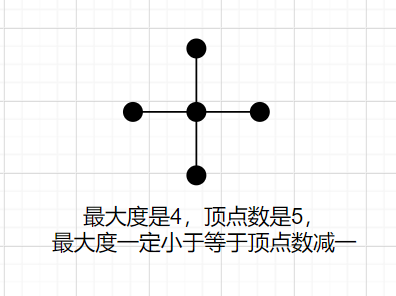
定理3：设G为任意n阶无向简单图，则$△(G)⩽n-1$。（$△(G)$代表最大度数，n代表顶点数(阶数)，一个图的最大度数一定小于等于顶点数减一）。

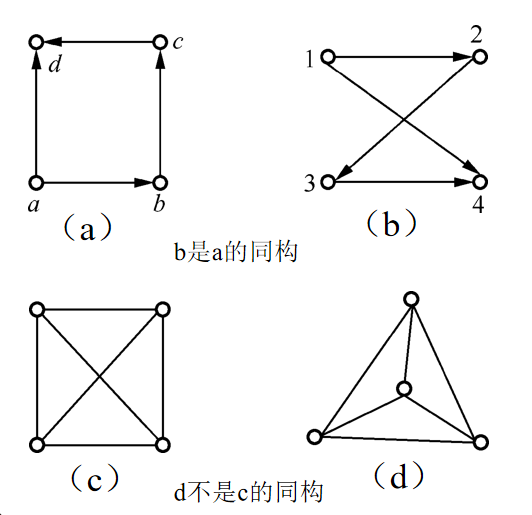
1.3 图的同构

定义：设G=(V, E),G′=(V′, E′)同为无向图或有向图, 若存在双射𝑓: V→V′, 使得:

• 对无向图, (𝑢, 𝑣)∈E⟺(𝑓(𝑢), 𝑓(𝑣))∈E′
• 对有向图, <𝑢, 𝑣>∈E⟺<𝑓(𝑢), 𝑓(𝑣)>∈E′
  且对应边重数相同, 则称G与G′是同构(Isomorphic)的, 记为G≅G′。

注意：由同构的定义可知, 不仅结点之间要具有一一对应关系, 而且要求这种对应关系保持结点间的邻接关系。对于有向图的同构还要求保持边的方向。

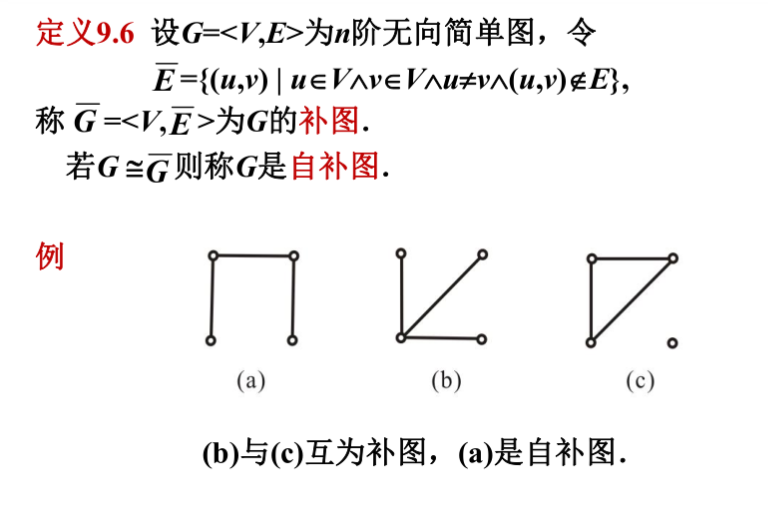
1.4 补图