“深度学习”学习日记。与学习相关的技巧 -- 参数的更新

news2025/12/5 19:14:24

2023.1.20

在神经网络的学习这一章，学习过了利用 梯度下降法 对参数进行更新，目的是找到是损失函数的值尽量小的参数；像解决这样的问题称为 最优化。

由于参数空间十分复杂、参数规模十分庞大，导致“最优化”的过程变得困难。

回忆一下随机梯度下降法（stochastic gradient descent），简称SGD

$W\leftarrow W-\eta \frac{\partial L}{\partial W}$ 、

将要更新的权重设置为W，把损失函数关于梯度几位 $\frac{\partial L}{\partial W}$ 。η 代表学习率；表示右边的值更新左边的值。

Python代码实现SGD：

class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):  # 为权重于偏置 w1，w2，b1，b2 这样的参数
        for key in params.key():
            params[key] -= self.lr * grads[key]

像这样单独实现进行最优化的类，功能的模块化变得简单：

import numpy as np
from collections import OrderedDict
from dataset.mnist import load_mnist
import sys, os

sys.path.append(os.pardir)


# 数值微分
def numerical_gradient(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)

    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])  # np.nditer() 迭代器处理多维数组
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = f(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2 * h)

        x[idx] = tmp_val  # 还原值
        it.iternext()

    return grad


# 损失函数
def cross_entropy_error(y, t):
    delta = 1e-7
    return -1 * np.sum(t * np.log(y + delta))


# 激活函数
def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x)
    return np.exp(x) / np.sum(np.exp(x))


def sigmoid(x1):
    return 1 / (1 + np.exp(-x1))


# 加法层、乘法层、激活函数层、Affine层、Softmax层
class Addyer:  # 加法节点
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y
        return out

    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1
        return dx, dy


class Mullyer:  # 乘法节点
    def __init__(self):  # __init__() 中会初始化实例变量
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = y
        self.y = x
        out = x * y

        return out

    def backward(self, dout):
        dx = dout * self.x
        dy = dout * self.y

        return dx, dy


class ReLU:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0

        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx


class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None
        self.t = None

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)

        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size

        return dx


class Affine:
    def __init__(self, w, b):
        self.w = w
        self.b = b
        self.x = None
        self.dw = None
        self.db = None

    def forward(self, x):
        self.x = x
        out = np.dot(x, self.w) + self.b

        return out

    def backward(self, dout):
        dx = np.dot(dout, self.w.T)
        self.dw = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)

        return dx


class TwoLayerNet:
    def __init__(self, input, hidden, output, weight__init__std=0.01):
        # 权重的初始化 假设一个权重
        self.params = {}
        self.params['w1'] = weight__init__std * np.random.randn(input, hidden)
        self.params['b1'] = np.zeros(hidden)
        self.params['w2'] = weight__init__std * np.random.randn(hidden, output)
        self.params['b2'] = np.zeros(output)

        # 生成层
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['w1'], self.params['b1'])
        self.layers['ReLU1'] = ReLU()
        self.layers['Affine2'] = Affine(self.params['w2'], self.params['b2'])

        self.lastlayer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    def loss(self, x, t):  # x:测试数据；t：监督数据
        y = self.predict(x)

        return self.lastlayer.forward(y, t)

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)  # 正确解标签
        if t.ndim != 1:
            t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    def numerical_grandient(self, x, t):  # x:测试数据；t：监督数据
        loss_w = lambda w: self.loss(x, t)

        grads = {}
        grads['w1'] = numerical_gradient(loss_w, self.params['w1'])
        grads['b1'] = numerical_gradient(loss_w, self.params['b1'])
        grads['w2'] = numerical_gradient(loss_w, self.params['w2'])
        grads['b2'] = numerical_gradient(loss_w, self.params['b2'])

        return grads

    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.lastlayer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        # reserved() 是 Python 内置函数之一，其功能是对于给定的序列（包括列表、元组、字符串以及 range(n) 区间），该函数可以返回一个逆序序列的迭代器（用于遍历该逆序序列）
        for layer in layers:
            dout = layer.backward(dout)

        # setting
        grads = {}
        grads['w1'] = self.layers['Affine1'].dw
        grads['b1'] = self.layers['Affine1'].db
        grads['w2'] = self.layers['Affine2'].dw
        grads['b2'] = self.layers['Affine2'].db

        return grads


# 随机梯度下降法
class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):  # 为权重于偏置 w1，w2，b1，b2 这样的参数
        for key in params.keys():
            params[key] -= self.lr * grads[key]


# 数据导入
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

networks = TwoLayerNet(input=784, hidden=50, output=10)
optimizer = SGD()

iters_num = 10000
train_size = x_train.shape[0]  # 60000
batch_size = 100  # 批处理数量
learning_rate = 0.1

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)  # mini——batch 处理
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    grads = networks.gradient(x_batch, t_batch)  # 通过误差反向传播法求梯度
    params = networks.params
    print(params, grads)
    optimizer.update(params, grads)

SGD的方法简单易于实现，但是也有缺点，现在通过一个函数来讲述：

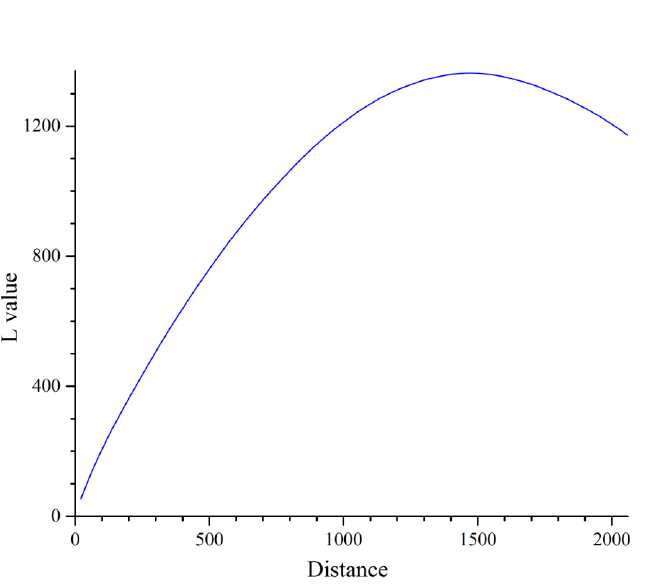
例如：函数 $f\left ( x,y\right )=\frac{1}{20}x^{2}+y^{2}$

利用Matlab绘制图像：

x = linspace(-10,10);

y = linspace(-10,10);

[X,Y] = meshgrid(x,y);

Z = (1/20)*X.^2+Y.^2;

Fig = mesh(X,Y,Z);

易得该函数的最低点在（0，0，0）处，从图中的颜色变化我们可以看到梯度特征，y轴方向上颜色变化大，意味着坡度大；x轴方向，颜色变化小，意味值梯度小；而SGD有一个重要的性质就是随机，假设从（x，y）=（-10，-10）开始搜索，SGD只会向一个梯度减少的方向前进，具体y轴方向、还是x轴方向都有可能。也就是说SGD低效的根本原因是，更新路径没有朝着最小值的方向前进。

所以现在学习一些更加高效的方法。

Momentum：

momentum是动量的意思，和物理有关：

表示方法： $v\leftarrow \alpha \upsilon -\eta \frac{\partial L}{\partial W}$ ； $W \leftarrow W +\upsilon$ ；

这里有一个新的变量 $\upsilon$ ，对应“速度”， $v\leftarrow \alpha \upsilon -\eta \frac{\partial L}{\partial W}$ 表示物体在梯度上受力，在这个力的作用下，物体的“速度”增加。

$v\leftarrow \alpha \upsilon -\eta \frac{\partial L}{\partial W}$ 中的 $\alpha \upsilon$ 这一项在物体不受力时，他承担时物体减速的任务，故 $\alpha$ 的值在[0,1] 这样的值：

代码实现：实例变量v会保存物体的速度。初始化时，self.v=None ，表示什么都不存，当update第一次执行时，v会以dict变量的形式保存于参数结构相关的数据

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]

与SGD相比，Momentum很大程度上减少了“随机”，如果SGD的更新路径是“Z”型随机，那么momentum的更新路是“S”型。因为x轴上的变化梯度很小，而y轴的变化梯度很大，可以看作x轴上受到的是恒力，而y轴上受到的是变力。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/173244.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！