c++数据结构-树（详细总结附代码，一看就懂）

news2024/10/7 8:25:07

树的定义

一棵树是由n（n>0）个元素组成的有限集合，其中：

（1）每个元素称为结点（node）

（2）有一个特定的结点，称为根结点或树根（root）

（3）除根节点外，其余节点能分成m（m>=0）个互不相交的有限集合 T(0)-T(m-1)。其中的每一个子集都是一个树，这些集合被称为这棵树的子树。

如下图是一棵树：

树的基本概念

A. 树是由递归定义的

B. 一棵树中至少有1个结点。这个节点就是根节点，他没有前驱，其余每个节点都有且只有一个前驱节点。每个节点可以有任意个后继结点。因此，树是非线性结构，但也是有序结构。

C. 一个节点的子树个数称为这个结点的度，例如上图根节点的度为2。度为0的结点被称为叶结点；度不为0的结点被称为分支结点，根以外的分支节点称为内部结点，树中各节点的度的最大值称为这棵树的度。

D. 在用图形表示的树形结构中，对两个用线段（我们称为树枝）连接的相关联的结点，称上端结点为下端节点的父节点，反之为子节点。

E. 定义一棵树的根的层次为1，其他结点的层次等于他的父节点的层次加一。一棵树中所有节点的层次的最大值称为这棵树的深度。

F. 对于树中任意两个不同的结点，从一个结点出发一定能到达另一个结点。

G.m（m>=0）棵树的结合称为森林。

树的遍历

在解决问题时，常常要按照某种次序来获取树中全部节点的信息，这种操作叫做树的遍历。

A. 先序遍历 先访问根节点，然后按照左右先后顺序遍历各子树（根左右）

B. 中序遍历 先访问左子树，然后访问根，最后访问右子树（左根右）

C. 层次遍历 按层次的大笑从小到大遍历，同一层次按照从左到右的顺序。

二叉树基本概念

二叉树（binary tree，简称BT），是一种特殊的树，它的度是2。一个节点有两个子节点，其中左边的是左子节点，右边的是右子节点。左边的叫左子树，右边的叫右子树。

二叉树的性质

（1）在二叉树的第 i 层上最多有 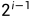个结点（i>=1）

（2）深度为 k 的二叉树至多有 个结点（k>=1）

特别的，深度为 k ，且有 个结点的二叉树称为满二叉树。

（3）对于任意一棵二叉树，如果其叶子结点数为 ，度为 2 的结点数为 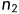，那么 。

（4）具有 n 个结点的完全二叉树的深度为 。

二叉树的实现

上面我们介绍了树和二叉树，那么我们现在研究一下二叉树的实现，注意，这里默认你有一些 C++ 基础。

首先我们来创建一个二叉树结点类 BSTNode，然后在类中创建几个 BSTNode 类型的变量，值，左子节点，右子节点，父节点。

int _key;  
BSTNode *_left;  //左子节点
BSTNode *_right; //右子节点
BSTNode *_parent;  //父节点

然后我们初始化，这里使用列表初始化。

BSTNode(int k = 0, BSTNode *l = NULL, BSTNode *r = NULL, BSTNode *p = NULL) : _key(k), _left(l), _right(r), _parent(p) {};

接下来，我们来创建一个二叉树类 BinaryTree ，来写二叉树的各种操作函数。

我们先声明函数

void insert(int _key);  //将_key节点插入到二叉树中
void PreOrder();  //前序二叉树遍历
void InOrder();  //中序二叉树遍历
void PostOrder();  //后序二叉树遍历

BSTNode *search(int _key);  //递归实现，在二叉树中查找_key节点
BSTNode *IteratorSearch(int _key);  //迭代实现，在二叉树中查找_key节点

BSTNode *successor(BSTNode *x);  //找节点(x)的后继节点。即，查找"二叉树中数据值大于该节点"的"最小节点"
BSTNode *predecessor(BSTNode *x);  //找节点(x)的前驱节点。即，查找"二叉树中数据值小于该节点"的"最大节点"

void remove(int _key);  //删除_key节点

void destroy();  //销毁二叉树

这里包括了二叉树的基本操作。

类的private部分：

BSTNode *_root;  //根节点
void PreOrder(BSTNode *tree); //前序二叉树遍历
void InOrder(BSTNode *tree);  //中序二叉树遍历
void PostOrder(BSTNode *tree);  //后序二叉树遍历

BSTNode *search(BSTNode *x, int _key);  //递归实现，在”二叉树x“中查找_key节点
BSTNode *IteratorSearch(BSTNode *x, int _key);  //迭代实现，在“二叉树x”中查找_key节点

BSTNode *minimum(BSTNode *tree);  //查找最小节点：返回tree为根节点的二叉树的最小节点
BSTNode *maximum(BSTNode *tree);  //查找最大节点：返回tree为根节点的二叉树的最大节点

void insert(BSTNode *&tree, BSTNode *z);  // 将节点(z)插入到二叉树(tree)中

BSTNode *remove(BSTNode *tree, BSTNode *z);  // 删除二叉树(tree)中的节点(z)，并返回被删除的节点

void destroy(BSTNode *&tree);  //销毁二叉树

也是声明了一些函数。

插入元素

void BinaryTree::insert(int _key)  //将_key节点插入到二叉树中
{
    BSTNode *z = new BSTNode(_key, NULL, NULL, NULL);
    if (z == NULL)
    {
        return;  
    }
    insert(_root, z); 
}
void BinaryTree::insert(BSTNode *&tree, BSTNode *z)  // 将节点(z)插入到二叉树(tree)中
{
    BSTNode *y = NULL;
    BSTNode *x = tree;
 
    while (x != NULL) 
    {
        y = x;
        if (z->_key < x->_key)
        {
            x = x->_left;
        }
        else
        {
            x = x->_right;
        }
    }
 
    z->_parent = y;
    if (y == NULL)
    {
        tree = z;
    }
    else
        if (z->_key < y->_key)
        {
            y->_left = z;
        }
        else
        {
            y->_right = z;
        }
}

首先创建一个结点，如果节点的值（key）是空（NULL）的话就结束函数，如果不为空的话就执行insert函数。insert函数的内容是循环树只要不为空，按照树的顺序找到合适的位置插入元素。

删除结点

BSTNode *BinaryTree::remove(BSTNode *tree, BSTNode *z)  // 删除二叉树(tree)中的节点(z)，并返回被删除的节点
{
    BSTNode *x = NULL;
    BSTNode *y = NULL;
 
    if (z->_left == NULL || z->_right == NULL)
    {
        y = z;
    }
    else
    {
        y = successor(z);
    }
 
    if (y->_left != NULL)
    {
        x = y->_left;
    }
    else
    {
        x = y->_right;
    }
 
    if (x != NULL)
    {
        x->_parent = y->_parent;
    }
 
    if (y->_parent == NULL)
    {
        tree = x;
    }
    else
        if (y == y->_parent->_left)
        {
            y->_parent->_left = x;
        }
        else
        {
            y->_parent->_right = x;
        }
 
    if (y != z)
    {
        z->_key = y->_key;
    }
    return y;
}
void BinaryTree::remove(int _key)  // 删除二叉树(tree)中的节点(z)，并返回被删除的节点
{
    BSTNode *z, *node;
    z = IteratorSearch(_root, _key); 
    if (z == _root){
        cout<<"Root can't be delete!"<<endl;
    }
    if (z != NULL && z->_parent != NULL && z != _root)
    {
        node = remove(_root, z);  
        if (node != NULL)
        {
            delete node;
        }
    }
}

销毁二叉树

void BinaryTree::destroy(BSTNode *&tree)  //销毁二叉树
{
    if (tree == NULL)
    {
        return; 
    }
    if (tree->_left != NULL)
    {
        return destroy(tree->_left);
    }
    if (tree->_right != NULL)
    {
        return destroy(tree->_right);
    }
    delete tree;
    tree = NULL;
}
 
 
void BinaryTree::destroy()  //销毁二叉树
{
    destroy(_root);
}

完整代码

/*
    文件创建者: 112233-星澜-imimbert
    创建日期: 2023.1.12 12:33
    功能: 二叉树
*/
#include <iostream>
using namespace std;
 
class BSTNode
{
public:
    int _key;  
    BSTNode *_left;  //左子节点
    BSTNode *_right; //右子节点
    BSTNode *_parent;  //父节点
     
    BSTNode(int k = 0, BSTNode *l = NULL, BSTNode *r = NULL, BSTNode *p = NULL) : _key(k), _left(l), _right(r), _parent(p) {};  //初始化列表
};
 
 
class BinaryTree
{
/****
    * @author 112233-imimbert-星澜
    * @since -verson: 1.0.0
    * @date 2021-01-12
    * @pre 二叉树已经创建
    * @include iostream
****/
public:
    BinaryTree();  
    ~BinaryTree();  
 
    void insert(int _key);  //将_key节点插入到二叉树中
    void PreOrder();  //前序二叉树遍历
    void InOrder();  //中序二叉树遍历
    void PostOrder();  //后序二叉树遍历
 
    BSTNode *search(int _key);  //递归实现，在二叉树中查找_key节点
    BSTNode *IteratorSearch(int _key);  //迭代实现，在二叉树中查找_key节点
 
    BSTNode *successor(BSTNode *x);  //找节点(x)的后继节点。即，查找"二叉树中数据值大于该节点"的"最小节点"
    BSTNode *predecessor(BSTNode *x);  //找节点(x)的前驱节点。即，查找"二叉树中数据值小于该节点"的"最大节点"
 
    void remove(int _key);  //删除_key节点
 
    void destroy();  //销毁二叉树
 
 
private:
    BSTNode *_root;  //根节点
    void PreOrder(BSTNode *tree);  //前序二叉树遍历
    void InOrder(BSTNode *tree);  //中序二叉树遍历
    void PostOrder(BSTNode *tree);  //后序二叉树遍历
 
    BSTNode *search(BSTNode *x, int _key);  //递归实现，在”二叉树x“中查找_key节点
    BSTNode *IteratorSearch(BSTNode *x, int _key);  //迭代实现，在“二叉树x”中查找_key节点
 
    BSTNode *minimum(BSTNode *tree);  //查找最小节点：返回tree为根节点的二叉树的最小节点
    BSTNode *maximum(BSTNode *tree);  //查找最大节点：返回tree为根节点的二叉树的最大节点
 
    void insert(BSTNode *&tree, BSTNode *z);  // 将节点(z)插入到二叉树(tree)中
 
    BSTNode *remove(BSTNode *tree, BSTNode *z);  // 删除二叉树(tree)中的节点(z)，并返回被删除的节点
 
    void destroy(BSTNode *&tree);  //销毁二叉树
};

 
BinaryTree::BinaryTree() :_root(NULL) {}; 
 
BinaryTree::~BinaryTree() 
{
    destroy();
}
 
 
void BinaryTree::insert(int _key)  //将_key节点插入到二叉树中
{
    BSTNode *z = new BSTNode(_key, NULL, NULL, NULL);
    if (z == NULL)
    {
        return;  
    }
    insert(_root, z); 
}
 
 
void BinaryTree::PreOrder(BSTNode *tree)  //前序二叉树遍历
{
    if (tree != NULL)
    {
        cout << tree->_key << " ";
        PreOrder(tree->_left);
        PreOrder(tree->_right);
    }
}
void BinaryTree::PreOrder()
{
    PreOrder(_root); 
}
 
 
void BinaryTree::InOrder(BSTNode *tree)  //中序二叉树遍历
{
    if (tree != NULL)
    {
        InOrder(tree->_left);
        cout << tree->_key << " ";
        InOrder(tree->_right);
    }
}
void BinaryTree::InOrder()
{
    InOrder(_root);  
}
void BinaryTree::PostOrder(BSTNode *tree)  //后序二叉树遍历
{
    if (tree != NULL)
    {
        PostOrder(tree->_left);
        PostOrder(tree->_right);
        cout << tree->_key << " ";
    }
}
void BinaryTree::PostOrder()
{
    PostOrder(_root);  
}
BSTNode *BinaryTree::search(BSTNode *x, int _key)  //递归实现，在”二叉树x“中查找_key节点
{
    if (x == NULL || _key == x->_key)
    {
        return x;
    }
    if (_key < x->_key)
    {
        return search(x->_left, _key);
    }
    else
    {
        return search(x->_right, _key);
    }
}
BSTNode *BinaryTree::search(int _key)
{
    return search(_root, _key);  
}
BSTNode *BinaryTree::IteratorSearch(BSTNode *x, int _key)  //迭代实现，在“二叉树x”中查找_key节点
{
    while (x != NULL && _key != x->_key)
    {
        if (_key < x->_key)
        {
            x = x->_left;
        }
        else
        {
            x = x->_right;
        }
    }
    return x;
}
BSTNode *BinaryTree::IteratorSearch(int _key)
{
    return IteratorSearch(_root, _key);  //传入根节点和待查找的关键字_key
}
BSTNode *BinaryTree::minimum(BSTNode *tree)  //查找最小节点：返回tree为根节点的二叉树的最小节点。
{
    if (tree == NULL)
    {
        return NULL;
    }
    while (tree->_left != NULL)
    {
        tree = tree->_left;
    }
    return tree;
}

BSTNode *BinaryTree::maximum(BSTNode *tree)  //查找最大节点：返回tree为根节点的二叉树的最大节点。
{
    while (tree->_right != NULL)
    {
        tree = tree->_right;
    }
    return tree;
}
BSTNode *BinaryTree::successor(BSTNode *x)  //找节点(x)的后继节点，也就是该节点的右子树中的最小节点
{
    BSTNode *y = NULL;
    if (x->_right != NULL)
    {
        return minimum(x->_right);  
    }
    y  = x->_parent;
    while (y != NULL && x == y->_right)
    {
        x = y;
        y = y->_parent;
    }
    return y;
}
 
 
BSTNode *BinaryTree::predecessor(BSTNode *x)  //找节点(x)的前驱节点是该节点的左子树中的最大节点。
{
    BSTNode *y = NULL;
    if (x->_left != NULL)
    {
        return maximum(x->_left);
    }
    y = x->_parent;
    while (y != NULL && x == y->_left)
    {
        x = y;
        y = y->_parent;
    }
    return y;
}
 
 
void BinaryTree::insert(BSTNode *&tree, BSTNode *z)  // 将节点(z)插入到二叉树(tree)中
{
    BSTNode *y = NULL;
    BSTNode *x = tree;
 
    while (x != NULL) 
    {
        y = x;
        if (z->_key < x->_key)
        {
            x = x->_left;
        }
        else
        {
            x = x->_right;
        }
    }
 
    z->_parent = y;
    if (y == NULL)
    {
        tree = z;
    }
    else
        if (z->_key < y->_key)
        {
            y->_left = z;
        }
        else
        {
            y->_right = z;
        }
}
 
 
BSTNode *BinaryTree::remove(BSTNode *tree, BSTNode *z)  // 删除二叉树(tree)中的节点(z)，并返回被删除的节点
{
    BSTNode *x = NULL;
    BSTNode *y = NULL;
 
    if (z->_left == NULL || z->_right == NULL)
    {
        y = z;
    }
    else
    {
        y = successor(z);
    }
 
    if (y->_left != NULL)
    {
        x = y->_left;
    }
    else
    {
        x = y->_right;
    }
 
    if (x != NULL)
    {
        x->_parent = y->_parent;
    }
 
    if (y->_parent == NULL)
    {
        tree = x;
    }
    else
        if (y == y->_parent->_left)
        {
            y->_parent->_left = x;
        }
        else
        {
            y->_parent->_right = x;
        }
 
    if (y != z)
    {
        z->_key = y->_key;
    }
    return y;
}
 
 
void BinaryTree::remove(int _key)  // 删除二叉树(tree)中的节点(z)，并返回被删除的节点
{
    BSTNode *z, *node;
    z = IteratorSearch(_root, _key); 
    if (z == _root){
        cout<<"Root can't be delete!"<<endl;
    }
    if (z != NULL && z->_parent != NULL && z != _root)
    {
        node = remove(_root, z);  
        if (node != NULL)
        {
            delete node;
        }
    }
}
 
 
void BinaryTree::destroy(BSTNode *&tree)  //销毁二叉树
{
    if (tree == NULL)
    {
        return; 
    }
    if (tree->_left != NULL)
    {
        return destroy(tree->_left);
    }
    if (tree->_right != NULL)
    {
        return destroy(tree->_right);
    }
    delete tree;
    tree = NULL;
}
 
 
void BinaryTree::destroy()  //销毁二叉树
{
    destroy(_root);
}


int main()
{
    /************************/
    /*          插入
    /************************/
    BinaryTree *tree = new BinaryTree();
    int array[6] = {12, 33, 18, 24, 44, 66};
    cout << "二叉树数值：" << endl;
    for (int i = 0; i < 6; i++)
    {
        cout << array[i] << " ";
        tree->insert(array[i]);  //调用插入函数，生成二叉查找树
    }
 
    cout << endl << endl;
 
 
    /************************/
    /*          遍历           
    /************************/
    cout << "前序遍历：";
    tree->PreOrder();
    cout << endl;
 
    cout << "中序遍历：";
    tree->InOrder();
    cout << endl;
 
    cout << "后序遍历：";
    tree->PostOrder();
    cout << endl << endl;
 
 
    /************************/
    /*          查找           
    /************************/
    int _keyword;  //查找节点的关键字
    cout << "请输入要查找的节点：";
    cin >> _keyword;
    cout << endl;
    BSTNode *node = tree->IteratorSearch(_keyword);  //获取数值的地址
    if (node)  //判断有没有地址
    {
        cout << "关键字为“" << _keyword << "”的节点，存在。" << endl ;
    }
    else
    {
        cout << "关键字为“" << _keyword << "”的节点，不存在。" << endl;
    }
    cout << endl << endl;
 
 
    /************************/
    /*          删除
    /************************/
    int DelNode;  //要删除的节点
    cout << "请输入要删除的节点：";
    cin >> DelNode;
    tree->remove(DelNode);
    cout << endl;
 
    cout << "删除操作后，(前序)遍历：";
    tree->PreOrder();
    cout << endl;
    cout << "删除操作后，(中序)遍历：";
    tree->InOrder();
    cout << endl;
    cout << "删除操作后，(后序)遍历：";
    tree->PostOrder();
    cout << endl << endl;
    
 
    /************************/
    /*          销毁
    /************************/
    tree->destroy();
    system("pause");
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/173057.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

上海亚商投顾：双创指数低开高走，数字经济继续活跃

上海亚商投顾：双创指数低开高走，数字经济继续活跃

上海亚商投顾前言&#xff1a;无惧大盘涨跌&#xff0c;解密龙虎榜资金&#xff0c;跟踪一线游资和机构资金动向&#xff0c;识别短期热点和强势个股。市场情绪三大指数今日低开高走&#xff0c;创业板指午后涨超1%&#xff0c;科创50指数涨超1.6%。数字经济概念继续爆发&#…
阅读更多...
算法基础（一）：时间复杂度和空间复杂度

算法基础（一）：时间复杂度和空间复杂度

算法基础&#xff08;一&#xff09;&#xff1a;时间复杂度和空间复杂度时间复杂度 O(1)O(1)O(1) O(N)O(N)O(N) O(logN)O(log N)O(logN) O(MN)O(MN)O(MN) O(NlogN)O(Nlog N)O(NlogN)、O(MlogN)O(Mlog N)O(MlogN) O(N2)O(N^2)O(N2)空间复杂度一些算法基础知识点和leetcode题解&…
阅读更多...
【网络通信】【电信运营商实战工程师】思科设备篇-思科设备企业网实战

【网络通信】【电信运营商实战工程师】思科设备篇-思科设备企业网实战

电信运营商实战工程师系列文章. 思科设备篇-思科设备企业网实战. 文章目录1. 思科设备基本开局配置2. ARP协议、交换机工作原理及广播风暴问题3. 思科设备 VLAN 及单臂路由实战4. 思科三层交换机实现 VLAN 间路由实战5. 思科设备静态默认及浮动路由实战6. 思科设备NAT实战全集1…
阅读更多...
YOLO_V8训练自己的数据集

YOLO_V8训练自己的数据集

YOLO_V8在2023年开年横空出世&#xff0c;在春节前还得卷一下。由于YOLO_V8和YOLO_V5是同一个作者&#xff0c;所以很多操作都是一样的&#xff0c;下面主要描述一下如何用自己的数据集进行训练和测试&#xff08;非命令行的方式&#xff09;。1、训练数据和模型的目录结构这里…
阅读更多...
设计模式学习（九）：Abstract Factory抽象工厂模式

设计模式学习（九）：Abstract Factory抽象工厂模式

目录 一、什么是Abstract Factory模式 二、Abstract Factory示例代码 2.1 类之间的关系 2.2 抽象的零件:ltem类 2.3 抽象的零件:Link类 2.4 抽象的零件:Tray类 2.5 抽象的产品: Page类 2.6 抽象的工厂:Factory类 2.7 使用工厂将零件组装称为产品:Main类 2.8 具体的工厂…
阅读更多...
linux三剑客之AWK

linux三剑客之AWK

目录 AWK是什么 AWK基本结构 a.txt的文本实例 AWK内置变量 a.txt的文本实例 AWK自定义变量 a.txt的文本实例 AWK内置函数 a.txt的文本实例 awk高级输出 a.txt的文本实例 排序输出 a.txt的文本实例 条件选择输出 a.txt的文本实例 控制语句 a.txt的文本实例 AWK是什…
阅读更多...
Java SE 继承和多态

Java SE 继承和多态

继承和多态 1. 继承 1.1 为什么需要继承 Java中使用类对现实世界中实体来进行描述&#xff0c;类经过实例化之后的产物对象&#xff0c;则可以用来表示现实中的实体&#xff0c;但是 现实世界错综复杂&#xff0c;事物之间可能会存在一些关联&#xff0c;那在设计程序是就需…
阅读更多...
Elasticsearch7.8.0版本高级查询—— 指定查询字段查询文档

Elasticsearch7.8.0版本高级查询—— 指定查询字段查询文档

目录一、初始化文档数据二、指定查询字段查询文档2.1、概述2.2、示例一、初始化文档数据 在 Postman 中&#xff0c;向 ES 服务器发 POST 请求 &#xff1a;http://localhost:9200/user/_doc/1&#xff0c;请求体内容为&#xff1a; {"name":"张三","…
阅读更多...
Git知识学习

Git知识学习

主要内容&#xff1a;熟练掌握Git、GitHub、GitLab、Gitee码云的使用 文章目录1.Git概述1.1版本控制1.2版本控制工具1.3Git和代码托管中心2.Git常用命令2.1设置用户签名2.2初始化本地库2.3查看本地库状态2.3.1首次查看2.3.2新增文件2.3.3再次查看2.4添加暂存区2.4.1将工作区文件…
阅读更多...
! LaTeX Error: File xxx.sty not found-统一解决办法

! LaTeX Error: File xxx.sty not found-统一解决办法

在使用一些模板时常见这个错&#xff0c;其实就是缺宏包&#xff01;解决方案如下&#xff01; 第一步&#xff1a;在网站 https://ctan.org/pkg 找到你缺失的宏包&#xff0c;下载zip文件。 第二步&#xff1a;将解压后的文件夹复制到安装路径下&#xff1a; 如&#xff…
阅读更多...
aws ecs 理解任务和容器的资源分配

aws ecs 理解任务和容器的资源分配

参考资料 如何在 Amazon ECS 中为任务分配内存&#xff1f; 关于 Amazon ECS 中的 CPU 分配&#xff0c;我需要了解哪些信息&#xff1f; Amazon ECS CloudWatch 指标 任务定义参数 在ecs中可以指定资源的分配逻辑&#xff0c;其实就是cpu和内存分配。 下面这张图对ecs任…
阅读更多...
搜索本地文件

搜索本地文件

李国春 处理大量的数据集时将文件整理到一起也是一个重要的工作。本文介绍一个将本地计算机目标文件的绝对路径汇集到一个文本文件的中的脚本。以方便后续批量处理这些文件。 启动RSD&#xff0c;在脚本编辑窗口输入图1中的代码。点击工具条上的小三角开始运行&#xff0c;提…
阅读更多...
计网必会：电子邮件、SMTP协议

计网必会：电子邮件、SMTP协议

文章目录SMTP概念SMTP的操作过程——发送邮件-接收邮件细品&#xff1a;发送邮件与HTTP的对比邮件报文格式和MIME邮件访问协议SMTP概念 SMTP是电子邮件中的主要协议&#xff0c;它能使用TCP可靠数据传输服务&#xff0c;从发送方的服务器向接收方发送邮件&#xff0c; SMTP&am…
阅读更多...
第四章必备前端基础知识-第二节1：CSS概述和选择器

第四章必备前端基础知识-第二节1：CSS概述和选择器

文章目录一&#xff1a;CSS概述&#xff08;1&#xff09;概述&#xff08;2&#xff09;语法规范&#xff08;3&#xff09;CSS引入方式二&#xff1a;选择器&#xff08;1&#xff09;基础选择器①&#xff1a;标签选择器②&#xff1a;类选择器③&#xff1a;id选择器④&…
阅读更多...
MyISAM存储引擎中的索引方案

MyISAM存储引擎中的索引方案

MyISAM存储引擎中的索引 我们知道 InnoDB存储引擎中索引即数据&#xff0c;也就是聚集索引的那棵B树的叶子节点中已经把所有完整的用户记录都包含了&#xff0c;而MyISAM引擎也使用BTree作为索引结构&#xff0c;但是却 将索引和数据分开存储&#xff0c;其特点如下&#xff1…
阅读更多...
ElasticSearch Docker 部署实例

ElasticSearch Docker 部署实例

文章目录前言基本环境构建Java安装docker安装es部署安装ES验证安装安装kibana设置密码进入es容器安装Vim修改es容器配置文件设置es访问密码设置Kibana密码理想状态方案二修改挂载安装IK分词器安装ik分词器在线安装离线安装前言 虽然说要停更&#xff0c;但是有些东西还是需要记…
阅读更多...
SpringMVC | SSM整合（SpringMVC+Spring+MyBatis）

SpringMVC | SSM整合（SpringMVC+Spring+MyBatis）

0️⃣概述&#x1f47e;SSM与三层架构对应关系SpringMVC —— 表示层&#xff08;controller、view&#xff09;Spring —— 业务逻辑层&#xff08;service&#xff09;MyBatis —— 数据访问层&#xff08;dao、pojo&#xff09;&#x1f47e;配置文件spring-config.xml ——…
阅读更多...
vue全家桶之vuex详解

vue全家桶之vuex详解

文章目录Vuex 概述1.1 组件之间共享数据的方式1.2 Vuex 是什么1.3 使用 Vuex 统一管理状态的好处什么样的数据适合存储到 Vuex 中2. Vuex 的基本使用3. Vuex 的核心概念3.1 核心概念概述3.2 State3.3 Mutation3.4 Action3.5 GetterVuex 概述 1.1 组件之间共享数据的方式 父向…
阅读更多...
NET.前端基础

NET.前端基础

均摘自C语言中文网 网页一般由三部分组成&#xff0c;分别是 HTML&#xff08;超文本标记语言&#xff09;、CSS&#xff08;层叠样式表&#xff09;和 JavaScript&#xff08;简称“JS”动态脚本语言&#xff09;&#xff0c;它们三者在网页中分别承担着不同的任务。 HTML …
阅读更多...
74. 搜索二维矩阵

74. 搜索二维矩阵

74.搜索二维矩阵一、题目描述二、解题思路2.1 二分查找行2.2 二分查找列三、提交结果一、题目描述 二、解题思路 采用两次二分的方式&#xff0c;第一次二分用于找到target在二维矩阵中的行标&#xff0c;第二次二分只需要对找到的行进行二分查找即可。 2.1 二分查找行 初始…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023