一、题目描述

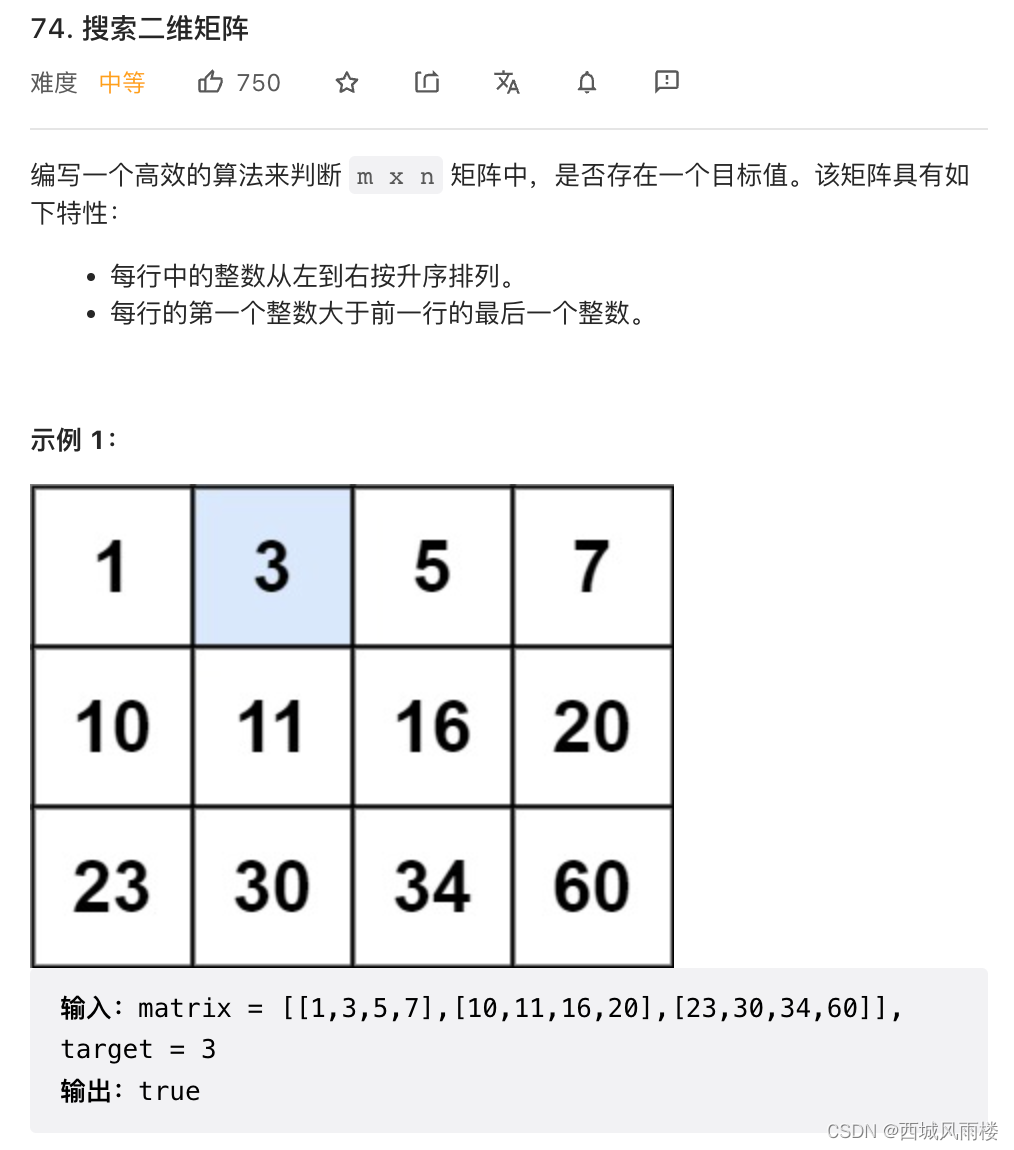
二、解题思路

采用两次二分的方式，第一次二分用于找到target在二维矩阵中的行标，第二次二分只需要对找到的行进行二分查找即可。

2.1 二分查找行

1. 初始时left = 0，表示第0行
2. right = martrix.length - 1，表示最后一行
3. 寻找left和right的中间位置mid=left + ((right - left) >> 1)
4. 令col = martrix[0].length，即col代表矩阵的列数
5. 如果martrix[mid][col - 1] < target，说明当前mid行的最后一个元素比target小，那么target一定在下一行，调整left = mid + 1
6. 如果martrix[mid][col - 1] > target，说明target要么在当前行，要么在前面的几行，此时可以再比较martrix[mid][0]和target的大小，如果比target大，那么target一定在前面几行，调整right = mid - 1
7. 否则说明target就在当前行，返回mid，如果找不到合适的行，说明不存在target

private int findRow(int[][] matrix, int target) {
        int left = 0;
        int right = matrix.length - 1;
        int col = matrix[0].length - 1;

        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (matrix[mid][col] < target) {
                left = mid + 1;
            } else if (matrix[mid][0] > target) {
                right = mid - 1;
            } else {
                return mid;
            }
        }

        return -1;
    }

2.2 二分查找列

知道目标值所在行之后，只需要对该行的数据二分查找target即可

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int row = findRow(matrix, target);
        if (row == -1) {
            return false;
        }
        return find(matrix[row], target);
    }

    private boolean find(int[] row, int target) {
        int left = 0;
        int right = row.length - 1;

        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (row[mid] == target) {
                return true;
            } else if (row[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return false;
    }

    private int findRow(int[][] matrix, int target) {
        int left = 0;
        int right = matrix.length - 1;
        int col = matrix[0].length - 1;

        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (matrix[mid][col] < target) {
                left = mid + 1;
            } else if (matrix[mid][0] > target) {
                right = mid - 1;
            } else {
                return mid;
            }
        }

        return -1;
    }
}

时间复杂度分析，如果矩阵的行为m，列为n，那么二分搜索行时间复杂度是O(logm)，确定行后，二分搜索该行元素时时间复杂度是O(logn)，所以时间复杂度是O(logm + logn)

三、提交结果