一些算法基础知识点和leetcode题解，来源于这里

时间复杂度

时间复杂度就是算法的执行效率，即：算法的执行时间与算法的输入值规模之间的关系。
一般不关心系数和小的时间。

大O表示法里面比较常见的时间复杂度：

· $O(1)$

执行时间与输入无关，没有循环

def O1(num):
	i = num  # 假设所用时间为a
	j = num * 2  # 假设所用时间为b
	return i+j  # 那么时间应该是a+b，是个常数，与nums无关，所以O(1)

· $O(N)$

def ON(num):
	total = 0
	for i in range(num):  # 有N个num
		total += i  # 假设所用时间为b
	return total  # 那么循环内部时间应该是Nb，忽略b，所以是O(N)

· $O(logN)$

常见于二分查找法

def OlogN(num):
	i = 1
	while (i<num):  # 有N个num
		i = i * 2  # 假设所用时间为a
	return i  # 循环内部循环了n次，2^n=N，所以n=log_2 N

循环内部循环了$n$次，$2^n=N$，所以$n\le lo{g}_{2}N$，比如，num=5时，i=2、4，循环了两次，所以循环内部时间应该是$alo{g}_{2}N$，最后用大O表示法就是$O(logN)$。

· $O(M+N)$

有两个循环，这两个循环不嵌套。

def OMN(num1, num2):
	total = 0
	for i in range(num1):  # 有N个num
		total += i  # 假设所用时间为b =>Nb
	for j in range(num2):  # 有M个num
		total += j  # 假设所用时间为c =>Mc
	return total  # 那么循环内部时间应该是Nb+Mc，忽略b、c，所以是O(M+N)

· $O(NlogN)$、$O(MlogN)$

常见于排序

def ONlogN(num1, num2):
	total = 0
	j = 1
	for i in range(num1):  # for循环内部是 M次
		while(j<num2):  # while循环内部是 log_2 N
			total += i + j
			j = j * 2
	return i

· $O(N^2)$

套了2个循环

def ON2(num):
	total = 0
	for i in range(num):  # N次
		for j in range(num):  # N次
			total += i + j
	return i

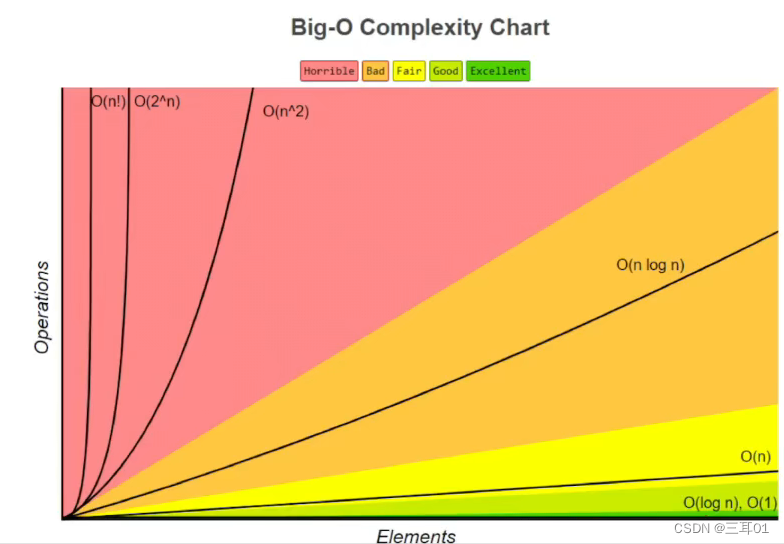
总结：其实重点就是看循环的次数

$$O(1)<O(logN)<O(N)<O(NlogN)<O(N^2)<O(2^N)<O(N!)$$

空间复杂度

也是用大O表示法表示。
空间复杂度指算法的存储空间与输入值之间的关系。

def test(num):
	total = 0  # 占了空间，空间就是一个int数字，所以O(1)
	for i in range(num):  # 不占空间，只是运行循环中的 i在循环结束的时候会被自动释放，所以可忽略。
		total += i
	return total

循环中的 i 在循环结束的时候会被自动释放，所以可忽略。所以空间复杂度就是O(1)

def test(nums):
	array = []  # 声明了变量，占空间
	for num in nums:
		array.append(num)  # nums有多大，array就有多大
	return array

存储的数据大小就是输入的大小。空间复杂度是O(N)。

空间复杂度就是找变量，如果变量是常量，那就是O(1)，所占用的空间是一定的，并不随着输入值的改变而改变。

常用的空间复杂度一般就是上面两种。
递归一般有一个O(N)的存储空间。

一般时间复杂度和空间复杂度只能选一点。工作中一般选时间复杂度最低的。