本篇仅用来记录
nn.Conv2d()中容易令人不解的几个参数
1. nn.Conv2d() 的输出维度的计算
相信大家都看过官网给出的计算方式:

直接套公式即可, 但需要注意的是, 最终计算的结果要向下取整.
2. dilation
官方解释为:
dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
翻译过来是卷积元素之间的间距. nn.Conv2d()中默认为1, 但是请注意, 1不是指卷积元素间隔为1, 而是间隔为0, 这个定义确实有点奇怪, 但也有人说如果按照stride理解就还好:

3. groups
字面意思可能不太好理解, 画个图就明白了:
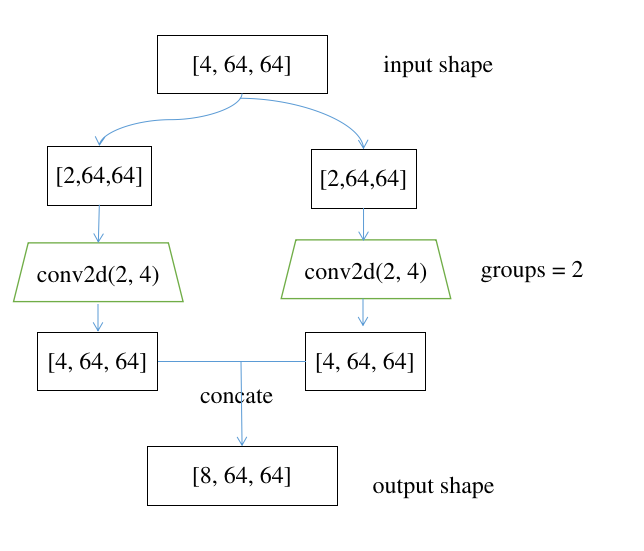
即,groups不为1时, conv2d就会拆成groups个,每一个的input channel等于原始输入的groups分之1, output channel也是原始输出的groups分之一(这也是要求groups必须能被input channel和output channel整除的原因), 最后会将各个conv2d的结果concate. groups参数并不影响最终输出的shape, 即以上跟conv2d(4, 8, groups=1)最终输出shape是一致的, 参考以下代码:
from torch import nn
x = torch.randn([4, 64, 64])
conv_grouped = nn.Conv2d(4, 8, 1, groups=2, bias=False)
output_grouped = conv_grouped(x)
print(output_grouped.shape)
conv1 = nn.Conv2d(2, 4, 1, bias=False)
conv2 = nn.Conv2d(2, 4, 1, bias=False)
output1 = conv1(x[:2,])
output2 = conv2(x[2:,])
output_manual = torch.cat((output1, output2), dim=0)
print(output_manual.shape)
输出:
torch.Size([8, 64, 64])
torch.Size([8, 64, 64])