455. 分发饼干

难度简单636

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

提示：

• 1 <= g.length <= 3 * 104
• 0 <= s.length <= 3 * 104
• 1 <= g[i], s[j] <= 231 - 1

贪心思路

本题分发饼干主要利用贪心算法,贪心算法的最主要思想就是局部最优推出全局最优.

什么意思呢 ? 举一个例子 ,现在有一堆钱,每次只能拿一张,每一个人只能拿5次,怎么拿钱数最多.

我想找这个谁都能想出来,每次拿钱都拿最大的--->局部最优, 最终拿完5次,我能拿到的最大钱数-->这个就是全局最优.  

遇到贪心问题,先要将一个大问题划分成多个小问题,然后让每一个小问题达到局部最优,最终解决了一个大问题(叠加小问题)就是全局最优

所以贪心思想可以分为如下几步

• 将一个大问题拆分成多个小问题
• 寻找合适的贪心解决方案
• 找到每一个小问题的最优解-->局部最优解
• 最终将每一个小问题的局部最优解堆叠成全局最优解.

分发饼干思路

根据题目分析,只要满足饼干尺寸大于小孩胃口尺寸就可以得到满足这个小孩的胃口,最终求的是怎样才能满足更多小孩的胃口.

我们要保证满足更多小孩的胃口,就要保证饼干不被浪费,所以可以有两种思路

第一种思路

• 大的饼干尺寸先分配给胃口大的小孩,从后往前遍历.->局部最优,尽可能分配饼干给更多的小孩->全局最优

第二种思路

• 小的饼干尺寸先分配给胃口小的小孩,从前往后遍历.->局部最优,尽可能分配饼干给更多的小孩->全局最优

局部最优解就是 让饼干不浪费,充分利用饼干尺寸喂饱一个尺寸

全局最优 : 尽可能分配饼干给更多的小孩

我使用的思路就是

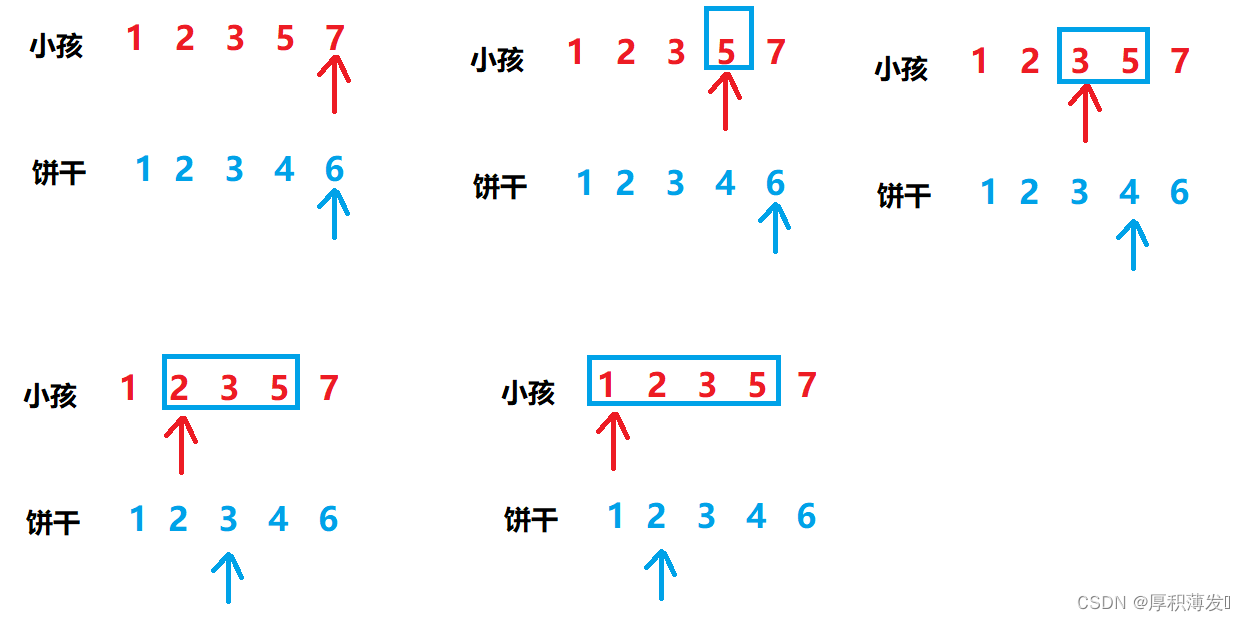
• 大饼干先满足胃口大的小孩.(因为要从后往前依次遍历,一定要给两个数组排序)

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int res = 0;
        // s:饼干尺寸s[j]  g:胃口的饼干最小尺寸g[i]  满足s[j]>=g[i]
        int i = g.length - 1;//小孩
        int j = s.length - 1;//饼干
        while(i>=0&&j>=0) {
           if(s[j]>=g[i]) {
               j--;
               i--;
               res++;
           }else {
               i--;
           }
        }
        return res;
    }
}