【数据结构】6.4 图的存储结构

news2024/9/9 7:34:21

文章目录

  • 6.4.1 邻接矩阵（数组）表示法
    • 无向图的邻接矩阵
      • 无向图邻接矩阵的特点
    • 有向图的邻接矩阵
      • 有向图邻接矩阵的特点
    • 网（有权图）的邻接矩阵
    • 采用邻接矩阵创建无向网
    • 邻接矩阵的优缺点
  • 6.4.2 邻接表（链式）
    • 无向图的邻接表
    • 有向图的邻接表
      • 邻接表
      • 逆邻接表
    • 图的邻接表存储表示
    • 采用邻接表表示法创建无向图
    • 邻接表表示法的优缺点
    • 邻接矩阵与邻接表示法的关系
  • 6.4.3 十字链表
  • 6.4.4 邻接多重表

  • 由于图的结构比较复杂，任意连个顶点之间都可能存在联系，因此无法以数据元素在存储区中的物理位置来表示元素之间的关系，即图没有顺序存储结构，但是可以借助二位数组来表示元素之间的关系，即邻接矩阵表示法。
  • 另一方面，由于图的任意两个顶点减都可能存在关系，因此，用链式存储表示图是很自然的事情，图的链式存储方式有多种，有==邻接表、十字链表、邻接多重表。

在这里插入图片描述

重点介绍：

  • 邻接矩阵（数组）表示法。
  • 邻接表（链式）表示法。

6.4.1 邻接矩阵（数组）表示法

建立一个顶点表（记录各个顶点的信息）和一个邻接矩阵（表示各个顶点之间的关系）

  • 假设图 A = (V,E) 有 n 个顶点，则：

在这里插入图片描述

  • 图的邻接矩阵是一个二维数组 A.arcs[n][n]，定义为：

在这里插入图片描述

无向图的邻接矩阵

图有 n 个顶点，这个邻接矩阵就用 n * n来表示。
因为要描述任意两个顶点之间的关系，任意两个顶点都需要描述它们两个之间有没有边。

下图有五个顶点，那么就需要一个 5*5的方阵。

  • 如果两个顶点之间存在邻接（有边）关系，那么邻接矩阵的值就是 1，反之为 0。

在这里插入图片描述

  • 先观察 V1，V1到V2、V4有边记为1，其余顶点没有边记为0。

在这里插入图片描述

  • 观察 V2，V2 到 V1、V3、V5 都有边记为1，其余记为0。

在这里插入图片描述

  • 之后再观察 V3、V4、V5 到其余各顶点的情况，最后就得到了这个图的邻接矩阵。

在这里插入图片描述

无向图邻接矩阵的特点

  1. 对角线上的值都是 0。
    • 因为对角线上都是每一个顶点和自身之间的关系，顶点没有到自身的边。

在这里插入图片描述

  1. 无向图的邻接矩阵是个对称矩阵。
    • 无向图的某两个顶点之间存在边，V1和V2之间是存在边，是邻接关系。同理V2和V1之间也存在着边，也是邻接关系。
    • 两个顶点之间如果有边，这两个顶点之间互为邻接关系。

在这里插入图片描述

  1. 顶点 i 的度 = 第 i 行（列）中为 1的个数。
    • 如：V1 所在的那一行有两个1，所以V1的度（与该顶点相关联的边的数量）为1。

特别：完全图的邻接矩阵中，对角元素为0，其余位1。

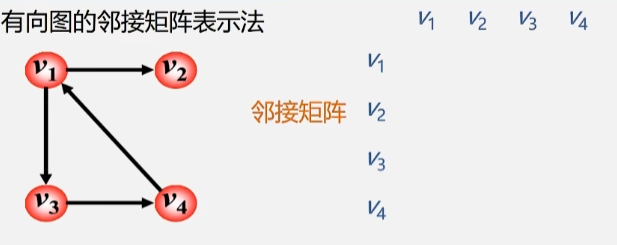
有向图的邻接矩阵

  • 首先，矩阵有几行几列任然取决于顶点的个数。
  • 在有向图中两个顶点之间的关系是有向的，顶点之间的边称作弧。

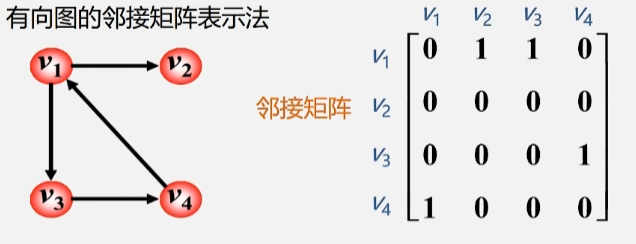
在这里插入图片描述

矩阵表示

如果存在着由当前顶点发出的弧，就在邻接矩阵当中记录一个1。没有发出弧的顶点在邻接矩阵中的值全为0。

  1. 从 V1 顶点出发，发出了两条弧，一条弧到 V2，一条弧到 V3，那么就在 V1 行的 V2 列和 V3 列记录一个1，其余记为 0。

在这里插入图片描述

  1. V2 顶点没有发出任何弧，那么从 V2 顶点到其他所有顶点的邻接矩阵的值都为0。

在这里插入图片描述

  1. 剩下的 V3 只发出来一条到 V4 的弧，V4 只发出了一条到 V1 的弧。

在这里插入图片描述

注：在有向图的邻接矩阵中

  • 第 i 行含义：以结点为 Vi 为尾的弧（即出度边）。
  • 第 i 列含义：以结点 Vi 为头的弧（即入度边）。

有向图邻接矩阵的特点

  1. 有向图的邻接矩阵可能是不对称的。
  2. 顶点的出度 = 第 i 行元素之和。顶点的入度 = 第 i 列元素之和。
    • V1 的出度就是看矩阵的第一行有多少1。
    • V1 的入度就是看矩阵的第一列有多少1。
  3. 顶点 i 的度 = 第 i 行元素之和 + 第 i 列元素之和。

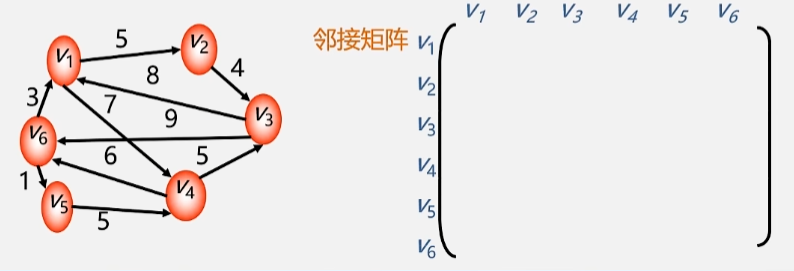
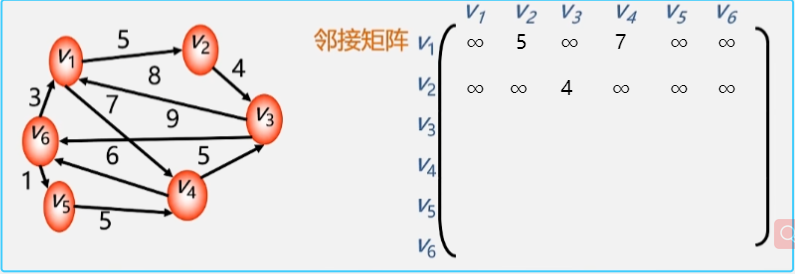
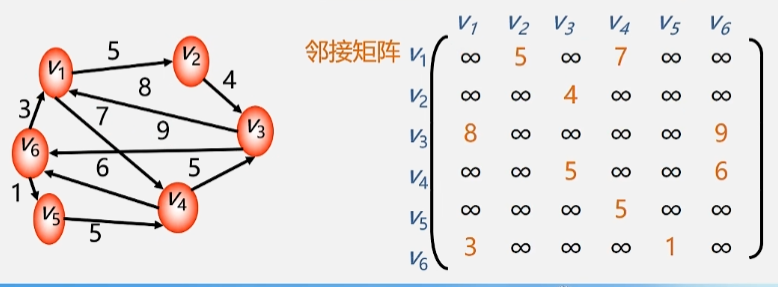
网（有权图）的邻接矩阵

网当中的边带有一个有特殊意义的值，这个值称为权值。

将网的邻接矩阵的值定义为：
在这里插入图片描述

  • 如果两个顶点之间存在着 边/弧，就在矩阵当中记录这两个顶点之间的边的权值。
  • 如果两个顶点之间不存在 边/弧，就在矩阵当中记录 ∞

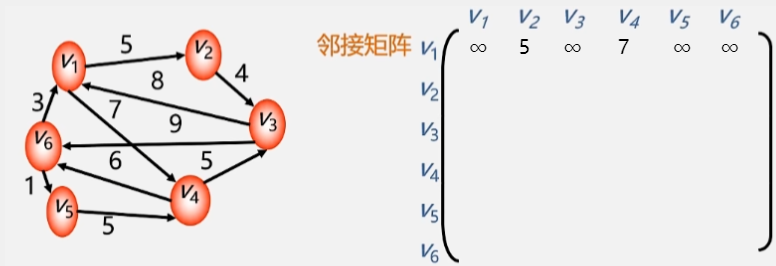
举个栗子

在这里插入图片描述

  1. 从 V1 出发的弧到各个顶点之间的权值记录为

在这里插入图片描述

  1. 从 V2 出发的弧到其余顶点的权值。

在这里插入图片描述

  1. 以此类推其余顶点到其他各个顶点的值

在这里插入图片描述

采用邻接矩阵创建无向网

邻接矩阵的存储表示：

  • 用两个数组分别存储顶点表（一维数组）和邻接矩阵（二维数组）。

形式定义

//图的邻接矩阵存储表示
#define MaxInt 32767 //表示极大值，即 ∞
#define MVNum 100   //最大顶点数

typedef char VerTexType;//假设顶点的数据类型为字符型
typedef int ArcType;//假设边的权值为整型

typedef struct
{
		VerTexType vexs[MVNum];//顶点表
		ArcType arcs[MVNum][MVNum];//邻接矩阵
		int vexnum;//图的当前点数
		int arcnum;//图的当前边数
	
}AMGraph；

无向网都搞定了的话，建立无向图、有向图、有向网只需要稍稍改动就可以了。

在这里插入图片描述

算法步骤

  1. 输入总顶点数和总边数。
  2. 依次输入点的信息存入顶点表中。
  3. 初始化邻接矩阵，使每个权值初始化为极大值。
  4. 构造邻接矩阵。依次输入每条边依附的顶点和其权值，确定两个顶点在图中的位置之后，使相应的边赋予相应的权值，同时使其对城边赋予相同的权值。

算法描述

//采用邻接矩阵表示法，创建无向网 G
Status CreatUDN(AMGrph &G)
{
		int i,j,k;
		
		cin >> G.vexnum >> G.arcnum;//输入总顶点数，总边数

		//依次输入顶点的信息
		for(i = 0;i < G.vexnum;i++)
		{
				cin >> G.vexs[i]);
		}	

		//初始化邻接矩阵，边的权值
		for(i = 0;i < G.vexnum;i++)
		{
				for(j = 0;j < G.vexnum;j++)
				{
						G.arcs[i][j] = MAXInt;每个值都先置为极大值
				}
		}		

		//构造邻接矩阵
		for(k = 0;k < G.arcnum;k++)
		{
				cin >> v1 >> v2 >> w;//输入一条边依附的顶点及权值
				//确定 v1和v2 在 G 中的位置，即顶点数组的下标
				i = LocateVex(G,v1);
				j = LocateVex(G,v2);
				G.arcs[i][j] = w;//边<v1,v2>的权值置为 w
				G.arcs[j][i] = G.arcs[i][j];//置<v1,v2>的对称边的权值为 w
		}
		return 0;
}

//补充算法，在图中查找顶点
int LocateVex(AMGraph G,VertexType u)
//在图 G 中查找顶点 u ，存在则返回顶点表中的下标，否则返回-1
{
		int i;
		for(i = 0;i <g.vexnum;i++)
		{
				if(G.vexs[i] == u)
				{
						return i;
				}
		}
		return -1;
}

算法分析

  • 该算法的时间复杂度是 O(n2)。
  • 若要建立无向图，只需要对上述算法做两处改动：
    • 一是初始化邻接矩阵时，将边的权值均初始化为 0。
    • 二是构造邻接矩阵时，将权值 w 改为常量值 1 即可。

邻接矩阵的优缺点

优点

  1. 直观、简单、好理解。
  2. 便于判断啊两个顶点之间是否有边，即根据 A[i][j] = 0 或 1来判断。
  3. 方便找人一顶点的所有 邻接点（有边直接相连的的顶点）。
  4. 便于计算各个顶点的度。
    • 对于无向图，邻接矩阵第 i 行元素之和就是顶点 i 的度；
    • 对于有向图，第 i 行元素之和就是顶点 i 出度，第 i 列元素之和就是顶点 i 的 入度。

缺点

  1. 不便于增加和删除顶点。
  2. 不便于统计边的数目，需要扫描邻接矩阵所有元素才能统计完毕，时间复杂度为 O(n2)。
  3. 空间复杂度高。
    • 如果是有向图：n 个邻接矩阵需要 n2 个单元存储边。
    • 如果是无向图：因其邻接矩阵时对称的，所以对规模较大的邻接矩阵可以采用压缩存储的方式，仅存储下三角（或上三角）的元素，这样需要 n(n-1)/2个单元即可。

6.4.2 邻接表（链式）

邻接表是图的一种链式存储结构。

  • 在邻接表中，对图中每个顶点啊 Vi 建立一个单链表，把与 VI 相邻接的顶点放在这个链表中。
  • 邻接表中每个单链表的第一个结点存放有关顶点的信息，把这一个结点看成链表的表头，其余结点存放有关边的信息，这样邻接表便由两部分组成：表头结点表和边表

在这里插入图片描述

表头结点表

由顶点构成的一维数组称为表头结点表

  • 表头结点包括数据域 (data) 和 链域（firstarc）。

在这里插入图片描述

  • 数据域用来存储顶点 Vi De 名称或其他有关信息。
  • 链域是用来指向链表中的第一个结点（即与顶点 Vi 邻接的顶点）。

边表

由表示图中顶点间关系的 2n 个边链表组成

  • 边链表中包含邻接点域 (adjvex) 和 链域 (nextarc)。

在这里插入图片描述

  • 邻接点域（adjvex）： 存放与 Vi 邻接的顶点在标表头数组中的下标，如： V1 的下一个邻接的顶点是位于数组下标 3 的 V4 顶点，然后 V1 顶点还到 位于下标 1 的 V2 有一条边。
  • 链域（nextarc）：链域指示与顶点 Vi 邻接的下一条边的结点。

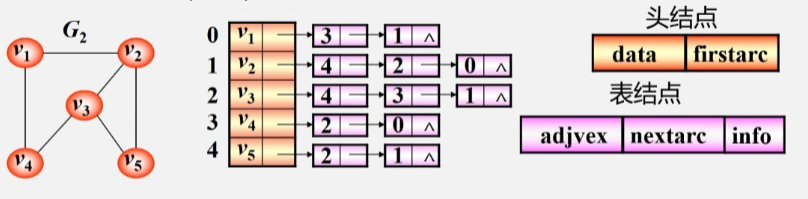
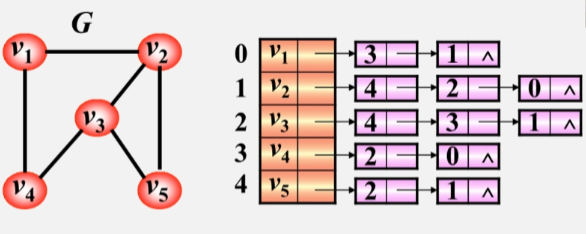
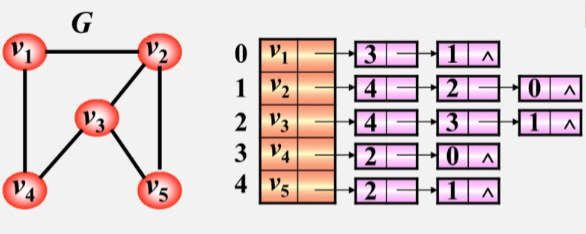
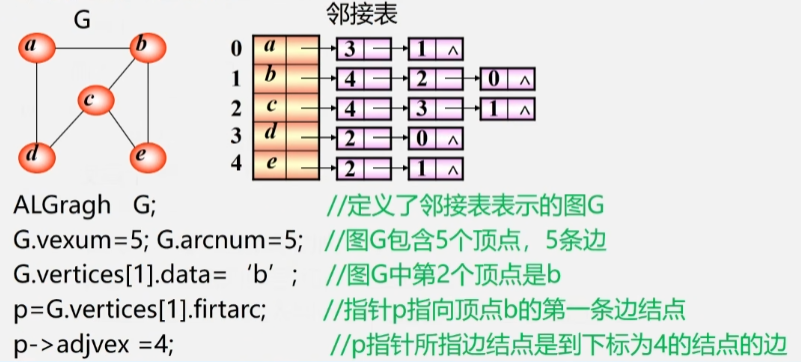
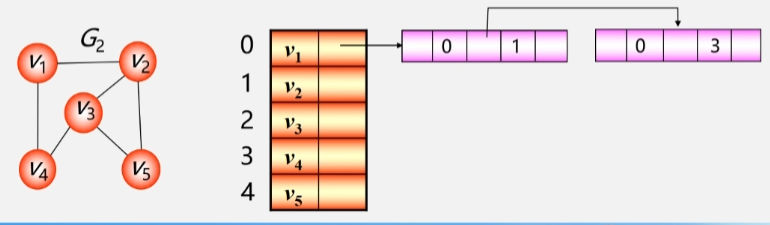
无向图的邻接表

在这里插入图片描述

  • 图 G 中有 5 个顶点，一维数组就开辟五个空间存储这些顶点。
  • 每个元素空间还有一个指针，用来指向与该顶点邻接的第一个邻接点。
  • 因为 下标 3 的 V4 是 V1 的邻接点，下标为 1 的 V2 也是 V1 的邻接点，所以 3、1 的位置是可以互换的。

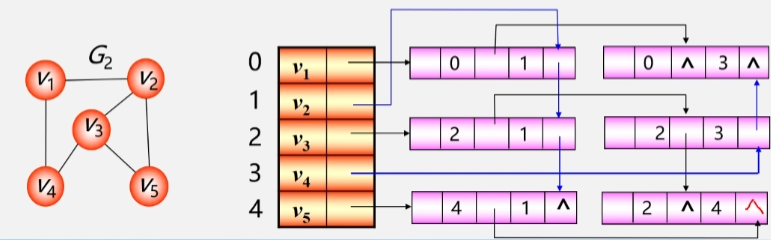
无向图邻接表的特点

在这里插入图片描述

  • 邻接表不唯一（与某个顶点连接的边的顺序是可变的）。
  • 若无向图中有 n 个顶点，e 条边。
    • 则其连接表需要 n 个头结点和 2e 个表结点。
    • 所以无向图邻接表需要 O(n + 2e) 的存储空间，适合存储稀疏图。
  • 无向图中顶点 Vi 的度为 第 i 个单链表中的结点数。
    • 每个顶点有多少个表结点，则和这个顶点关联的边就有几个。
    • 如：V1 有 2 个表结点，所以和V1 关联的边有两条，V1 的度为2

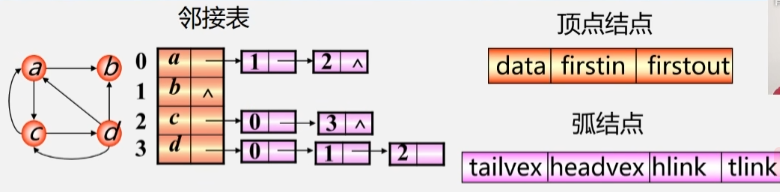
有向图的邻接表

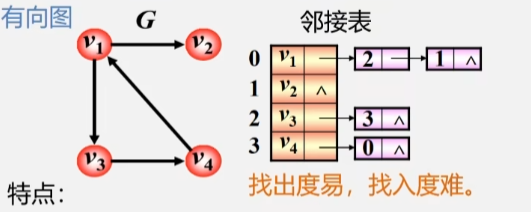
邻接表

在这里插入图片描述

在有向图中，只需要保存以当前顶点为弧尾的这一条边。没有发出弧的顶点的头结点表的链域就置为NULL。

有向图邻接表的特点

  • 顶点 Vi 的 出度为第 i 个单链表中的结点个数。
  • 顶点 Vi 的入度为整个单链表中邻接点域置是 i-1 的结点个数。

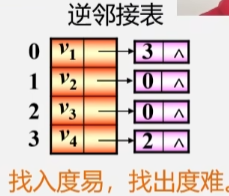
逆邻接表

既然可以用每个结点来存储顶点的出度边，那么当然也能反过来存入度边。

  • 在逆邻接表中，单链表当中的加点是入度边

在这里插入图片描述

有向图逆邻接表的特点

  • 顶点 Vi 的入度为第 i 个单链表中的结点个数。
  • 顶点 Vi 的出度为整个单链表中邻接点域是是 i-1 的结点个数。

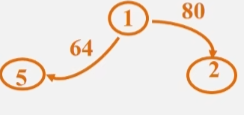
练习：请画出某网的邻接（出边）表，请画出该网络。
从出边可以得知，这是个有向网

在这里插入图片描述

  • 每一个单链表都是一个以当前顶点为弧尾。
    • 如：以顶点1为弧尾的出度弧有两条，分别邻接 2 顶点和 5 顶点。

在这里插入图片描述

  • 依次找到所有的顶点出发的到其他顶点的弧，有向网就画出来了。

在这里插入图片描述

图的邻接表存储表示

顶点的结点结构定义

在这里插入图片描述

//顶点结构定义
typedef struct VNode 
{//顶点的结构包含两个成员
		
		VerTexType data;//顶点的数据域，用来存储顶点信息
		ArcNode* firstarc;//指向边结点的一个指针
		
}VNode,AdjList[MVNum];//AdjList 表示邻接表类型
//说明：例如，AdjList v; 相当于：VNode v[MVNum]

弧（边）的结点结构定义

在这里插入图片描述

//边结点的结构定义
#define MVNum 100 //最大顶点数
typedef sturct ArcNode //边结点
{
		int adjvex;//指向相邻的邻接点位置的下标
		struct ArcNode* nextarc;//指向自身结点结构的指针
		OtherInfo info;//和边相关的信息，如：权值
		
}ArcNode;

图的结构定义

typedef struct
{
		AdjList vertices;//邻接表类型的数组，存储所有的顶点
		int vexnum;//图的当前顶点数
		int arcnum;//图的当前弧数

}ALGraph;

邻接表操作举例

在这里插入图片描述

采用邻接表表示法创建无向图

算法步骤

  1. 输入总顶点数和总边数。
  2. 建立顶点表。
    • 依次输入点的信息存入顶点表中。
    • 使每个表头结点的指针域初始为NULL。
  3. 创建邻接表
    • 依次输入每条边连接的两个顶点。
    • 查找这两个顶点的序号 i 和 j ，建立边结点。
    • 将此边结点分别插入到 Vi 和 Vj 对应的两个边链表的头部。

算法描述

//采用邻接表表示法，创建无向图 G
Status CreateUDG(ALGraph &G)
{
		cin >> G.vexnum >> G.arcnum;//输入总定点数，总边数
		
		for(i = 0;i < G.vexnum;i++)//输入各点，构造表头结点表
		{
				cin >> G.vertices[i].data;//输入顶点值
				G.vertices[i].firstarc = NULL;/初始化表头结点的指针域为 NULL
				
		}
		for(k = 0;k < G.arcnum;k++)//输入各边，构造邻接表,数组中有几个顶点就循环多少次
		{
				cin >> v1 >> v2;//输入一条边连接的两个顶点
				
				//确定 V1 和 V2 在G中的位置，即顶点G.vertices中的序号	
				i = LocateVex(G,v1);
				j = LocateVex(G,v2);
				
				p1 = nex ArcNode;//生成一个新的边结点*p1
				p1->adjvex = j;//邻接带你序号为j
				
				//将新结点*p1插入到顶点Vi的边表头部
				p1->nextarc = G.vertices[i].firstarc;
				G.vertices[i].firstarc = p1;

				p2 = nex ArcNode;//生成另一个对称的新的边结点*p2
				p2->adjvex = i;//邻接点序号为i

				//将新结点*p2插入到顶点Vj的边表头部
				p2->nextarc = G.vertices[j].firstarc;
				G.vertices[j].firstarc = p2;
		}
		
		return OK;
}

算法分析

  • 该算法的时间复杂度是O(n+e)

邻接表表示法的优缺点

优点

  1. 便于增加和删除顶点。
  2. 便于统计边的数目，按顶点表顺序扫描所有边表即可得到边的数目，其时间复杂度为 O(n+e)。
  3. 空间效率高 对于一个具有 n 个顶点 e 条边的图 G：
    • 若 G 是无向图：则在其邻接表表示中有 n 个顶点表结点和 2e 个边表结点。
    • 若 G 是有向图：则在它的邻接表表示或逆邻接表表示中均有 n 个顶点表结点和 e 个边表结点

缺点

  1. 不便于判断顶点之间是否有边，要判定 Vi 和 Vj 之间是否有边，就需要扫描第 i 个边表，最坏的情况下要耗费 O(n) 的时间。
  2. 不便于计算各个顶点的度：
    • 对于无向图：在邻接表表示中顶点 Vi 的度是第 i 个边表中的结点个数。
    • 对于有向图：在第 i 个边表上的结点个数是顶点 Vi 的出度，但是求 Vi 的入度比较困难。
      • 若有向图采用逆邻接表表示，则与邻接表表示相反，求顶点的入度容易，求出度难。

邻接矩阵与邻接表示法的关系

联系：

在这里插入图片描述

邻接表中每个链表对应于邻接矩阵中的一行，链表中接地那个数等于一行中非零元素的个数

  • 对于邻接矩阵：顶点 Vi 所在的第 i 行有几个 1，就表示顶点 Vi 有几条边。
  • 对于邻接表：顶点 Vi 的边结点有几个，则表示 Vi 有几条边。

区别：

  1. 对于任一确定的无向图，邻接矩阵是唯一的（行列号与顶点编号一直），但邻接表不唯一（链接次序与顶点编号无关）。
  2. 邻接矩阵的空间复杂度为O(n2)，而邻接表的空间复杂度为O(n+e)
  3. 用途：邻接矩阵多用于稠密图；而邻接表多用于稀疏图（边比较少）。

6.4.3 十字链表

在这里插入图片描述

  • 十字链表是有向图的另一种链式存储结构。可以看成是将有向图的邻接表以及逆邻接表结合起来得到的一种新的链表。

在这里插入图片描述

  • 同时有向图中的每个顶点在十字链表中对应有一个结点，叫做顶点结点，用来存放原来的第一个出、入度边。

在这里插入图片描述

  • 有向图中的每一条弧对应十字链表中的一个弧结点。

在这里插入图片描述

补充

在这里插入图片描述

  1. 顶点结点的第二个元素指向该顶点的入度弧，第三个元素指向该顶点的出度弧。

    • 因此顶点结点的第二个元素会指向箭头指向该顶点的那条弧。
    • 因此顶点结点的第三个元素会指向箭头来自该顶点的那条弧。

  2. 一个弧结点就代表着一条弧。

    • 第一个元素（tailvex）代表这个弧来自于哪个顶点。
    • 第二个元素（headvex）代表这条弧指向哪个顶点。
    • 第三个元素（hlink）指向下一个指向同一个顶点的弧。
    • 第四个元素（tlink）指向下一条同一个顶点发出的弧。

6.4.4 邻接多重表

在这里插入图片描述

邻接表

  • 优点：容易求得顶点和边的信息，
  • 缺点：某些操作不方便（如：删除一条边需找表示此结边的两个结点）。

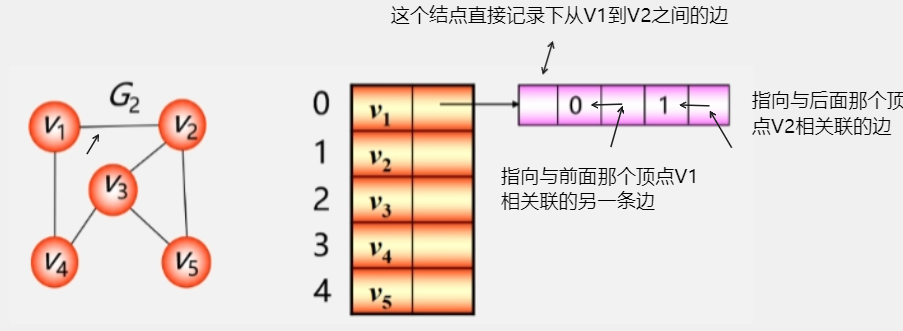
在这里插入图片描述

邻接多重表

在这里插入图片描述

在邻接多重表中，每一条边用一个边结点表示。

  • 这样一个边结点就存储了从 0 号位置的 V1 到 1号位置的 V2 之间的边。
  • 下次就不用再记录从 V2 到 V1 之间的边了，直接使用这个边结点即可。

在这里插入图片描述

  • 从 V1 到 V4 之间还有一条边，继续用一个边结点记录下来。这两条边都是从 0 号位置的 V1 开始的。
    • 想找与 V1 相关的边就只需要找到第一条边就行了。

在这里插入图片描述

  • 之后再找与 V2 相关联的边，V2 - V1 这条边已经有了，不需要再找一次了，直接拿来用，去找其余和 V2 有关联的边。

在这里插入图片描述

  • 依次类推找到所有与其余顶点相关联的边。

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/172842.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【人工智能原理自学】初识Keras：轻松完成神经网络模型搭建

【人工智能原理自学】初识Keras：轻松完成神经网络模型搭建

&#x1f60a;你好&#xff0c;我是小航&#xff0c;一个正在变秃、变强的文艺倾年。 &#x1f514;笔记来自B站UP主Ele实验室的《小白也能听懂的人工智能原理》。 &#x1f514;本文讲解初识Keras&#xff1a;轻松完成神经网络模型搭建&#xff0c;一起卷起来叭&#xff01; 目…
阅读更多...
Eureka入门

Eureka入门

Eureka入门Eureka入门什么是Eureka构建项目demo服务拆分远程调用创建Pom聚合工程Eureka使用搭建注册中心注册服务远程调用出现的问题Eureka入门 什么是Eureka Eureka是SpringCloud提供的注册中心&#xff0c;用来解决微服务之间远程调用问题&#xff0c;如&#xff1a; 消费…
阅读更多...
交通流的微观模型研究（Matlab代码实现）

交通流的微观模型研究（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…
阅读更多...
Redis原理篇（四）内存回收

Redis原理篇（四）内存回收

Redis之所以性能强&#xff0c;最主要原因是基于内存存储。但是单节点的Redis其内存大小不宜过大&#xff0c;会影响持久化或主从同步性能。 可以通过配置文件来设置最大内存 # maxmemory <bytes> maxmemory 1gb一、过期策略 可以通过expire命令给Redis的key设置TTL …
阅读更多...
【C++算法图解专栏】一篇文章带你掌握高精度加减乘除运算

【C++算法图解专栏】一篇文章带你掌握高精度加减乘除运算

✍个人博客&#xff1a;https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 &#x1f4e3;专栏定位&#xff1a;为 0 基础刚入门数据结构与算法的小伙伴提供详细的讲解&#xff0c;也欢迎大佬们一起交流~ &#x1f4da;专栏地址&#xff1a;https://blog.csdn.net/Newin…
阅读更多...
Java 异常 笔记

Java 异常 笔记

异常体系结构 异常分为Error和Exception。Error通常是灾难性错误&#xff0c;一般发生时&#xff0c;JVM选择终止程序执行&#xff1b;Exception通常可在程序中进行处理&#xff0c;尽量避免 Exception分支中有一个重要子类RuntimeException&#xff0c;运行时异常 ArrayInd…
阅读更多...
数据库，计算机网络、操作系统刷题笔记34

数据库，计算机网络、操作系统刷题笔记34

数据库&#xff0c;计算机网络、操作系统刷题笔记34 2022找工作是学历、能力和运气的超强结合体&#xff0c;遇到寒冬&#xff0c;大厂不招人&#xff0c;可能很多算法学生都得去找开发&#xff0c;测开 测开的话&#xff0c;你就得学数据库&#xff0c;sql&#xff0c;oracle…
阅读更多...
深入理解Promise

深入理解Promise

Promise的前提概念 Promise是一个构造函数&#xff0c;用来生成Promise实例 Promise构造函数接受一个函数作为参数&#xff0c;该函数有两个参数&#xff0c;分别是resolve和reject resolve&#xff1a;成功时的回调 reject&#xff1a;失败时的回调 Promise分别有三个状态 1…
阅读更多...
行人属性识别研究综述（一）

行人属性识别研究综述（一）

文章目录摘要1、简介2 问题的表述和挑战3 标准3.1 数据集3.2 评价标准4 行人属性识别的常规流程4.1 多任务学习4.2 多标签学习5 深度神经网络&#x1f407;&#x1f407;&#x1f407;&#x1f407;&#x1f407;&#x1f407;&#x1f407; 欢迎阅读 【AI浩】 的博客&#x1f…
阅读更多...
C#上位机基础学习_基于S7.Net实现读取S7-1500PLC中的字符串变量

C#上位机基础学习_基于S7.Net实现读取S7-1500PLC中的字符串变量

C#上位机基础学习_基于S7.Net实现读取S7-1500PLC中的字符串变量 如下图所示，首先在TIA博途中创建一个项目，添加一个1500PLC，添加一个DB块，在DB块中添加几个字符串变量， 如下图所示，打开Visual Studio 2019，新建一个项目，在Form1中添加一个按钮和一个文本框， 如下图…
阅读更多...
linux——高级信号

linux——高级信号

高级信号的收发发&#xff1a;siquequ收&#xff1a;sigaction() 包含三个元素num,sigaction()函数&#xff0c;备份num ->signumsigaction是一个结构体&#xff0c;需额外配置再传进来备份直接忽略&#xff0c;代表不需要备份sigaction结构体又包含四个元素sa_handler&…
阅读更多...
Git进阶：修改上次提交 git commit --amend

Git进阶：修改上次提交 git commit --amend

一、问题说明 git commit 后&#xff0c;发现刚才的备注写错了&#xff0c;或者代码漏掉了&#xff0c;这时我们肯定是想取消刚才的提交。此刻有两种方法 &#xff08;1&#xff09;使用git reset命令将刚才的提交会退掉。需要注意的是git reset --soft 和git reset --hard的区…
阅读更多...
【附源码】国内首届Discord场景创意编程开源项目

【附源码】国内首届Discord场景创意编程开源项目

以下开源项目是由环信联合华为举办的《国内首届Discord场景创意编程赛》作品&#xff0c;附源码&#xff0c;一键即用。 一、 模拟器游戏直播-新新人类 新新人类模拟器游戏直播基于环信超级社区Demo构建&#xff0c;增加以“video-x”命名的新型Channel&#xff0c;用户可在本…
阅读更多...
Java三目运算符导致 NPE

Java三目运算符导致 NPE

在三目运算符中&#xff0c;表达式 1 和 2 在涉及算术计算或数据类型转换时&#xff0c;会触发自动拆箱。当其中的操作数为 null 值时&#xff0c;会导致 NPE 。 一、基础知识 三目运算符 三目运算符是 Java 语言中的重要组成部分&#xff0c;它也是唯一有 3 个操作数的运算…
阅读更多...
Linux常用命令——tempfile命令

Linux常用命令——tempfile命令

在线Linux命令查询工具(http://www.lzltool.com/LinuxCommand) tempfile shell中给临时文件命名 补充说明 有时候在写Shell脚本的时候需要一些临时存储数据的才做&#xff0c;最适合存储临时文件数据的位置就是/tmp&#xff0c;因为该目录中所有的内容在系统重启后就会被清…
阅读更多...
LInux（三）程序地址空间、内存管理

LInux（三）程序地址空间、内存管理

目录 一、程序地址空间 二、内存管理方式 1、分段式内存管理 2、分页式内存管理 3、段页式内存管理 三、关于内存管理内容补充&#xff08;分页式&#xff09; 1、页表简单呈现 2、访问权限位 3、缺页中断 4.内存置换算法 一、程序地址空间 创建父子进程同时访问同一变量…
阅读更多...
正式发布丨Azure OpenAI Service

正式发布丨Azure OpenAI Service

Azure OpenAI 服务现已在微软全球 Azure 平台正式发布&#xff0c;这是微软人工智能大众化以及与 OpenAI 持续合作的又一里程碑。 大型语言模型正迅速成为用户无限创新、应用 AI 解决重要问题的平台。随着 Azure OpenAI 服务的正式发布&#xff0c;更多企业用户可以访问世界先…
阅读更多...
在线支付系列【5】支付安全之数字证书

在线支付系列【5】支付安全之数字证书

有道无术&#xff0c;术尚可求&#xff0c;有术无道&#xff0c;止于术。 文章目录公钥信任问题数字证书颁发流程使用流程SSL数字证书HTTPSSSL/TLS 证书如何申请SSL 证书使用keytool 生成ssl证书通信过程公钥信任问题 之前我们使用对称、非对称加密、信息摘要、数字签名&#…
阅读更多...
DPDK系列之一基础环境搭建

DPDK系列之一基础环境搭建

一、DPDK是什么 DPDK,Data Plane Development Kit&#xff0c;数据平面开发套装&#xff0c;它还有一个兄弟SPDK&#xff0c;专门用来做存储优化的。它主要运行于Linux&#xff0c;是由Intel几家公司共同开发&#xff0c;用于快速处理数据的一个网络开发工具套装。更详细的说明…
阅读更多...
python数据清洗1

python数据清洗1

数据获取——》数据清洗——》数据转换——》数据分析 通过设置步长&#xff0c;有间隔的取元素通过设置步长为-1&#xff0c;将元素颠倒 数据清洗工具 目前在Python中, numpy和pandas是最主流的工具。 Numpy中的向量化运算使得数据处理变得高效&#xff1b;Pandas提供了大量…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023