目录

前言

一、哈希切割

题目一

解法一：哈希切割

二、位图的应用

题目一：

解法一：哈希切割

解法二：双位图

 解法三：单位图（进阶版）

题目二

解法一：哈希切割

 解法二：位图

题目升华：怎么求交集？并集？差集？

思路：

问题一：交集

问题二：并集

问题三：差集

题目三

解法一：哈希切割

解法二：使用2个位图

三、布隆过滤器

题目一

精确算法：哈希切割

近似算法：布隆过滤器

题目二

解法一：计数器

---

前言

        对于大公司来说，面试考到的频率较高，请自行斟酌！

---

一、哈希切割

题目一

        给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？ 与上面条件相同， 如何找到top K的IP？

        

思考一下难点：

        通常如果忽略大小，我们可以统计每一个IP出现的次数，因为可以使用Map来统计数量。但是目前最大的问题是100G的数据太大，除非是超级计算机，否则也不乏一次性将这些数据加载到内存当中；

思路：

        既然数据太大，咱们就把他拆分成若干个小文件，但是怎么拆分呢？均分可以吗？不可以的，因为均分会出现一个情况，一个文件中最多的IP地址，不一定就是整体上最多的IP地址，所以不可以均分（均分的是数量，不是IP地址的内容均分的）。

那么换一种思路，将相同的IP存储到同一个文件中，那么只需要统计每个文件中的最大值，每一个文件都知道了，那么第topK个还是问题吗？所以最后就能实现题目要求；

解法一：哈希切割

        1.IP本身就是一个字符串，可以经过hash把IP变成一个整数；

        2.文件的下标index = 刚刚所得到的整数 % 200（相当于分成200份）如下图：

这样做的好处：

        可以把相同的字符串映射到同一个文件中；

最后：

        使用Map统计每一个文件中IP出现的次数；

---

二、位图的应用

题目一：

给定100亿个整数，设计算法找到只出现一次的整数？

思考一下难点：

        100亿个整形数据，肯定存在重复的整数，并且100亿个整数相当占40G的内存；

解法一：哈希切割

        把每个数字都哈希到对应的小文件中，一样的数字肯定是在一起的，遍历每一个小文件，统计数字出现的次数，此时，在内存中就能直到，那些数字只出现了一次；

解法二：双位图

        创建两个位图，用两个位图相同下标的的位置表示一个数字出现的次数，如果是（0，0）表示没出现，（0，1）表示出现一次，（1，0）表示出现两次，（1，1）表示出现三次或以上，例如下图：

 解法三：单位图（进阶版）

        两个位图可以用分别用两个bit位来表示，那么一个位图该怎么表示呢？一样的道理，每次拿出两个bit位来表示一个数字出现的次数，但是要注意的是，这里我们定位下标就不能在像以前那样除8模8了，而是除4模4再乘2，如下图：

题目二

给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

解法一：哈希切割

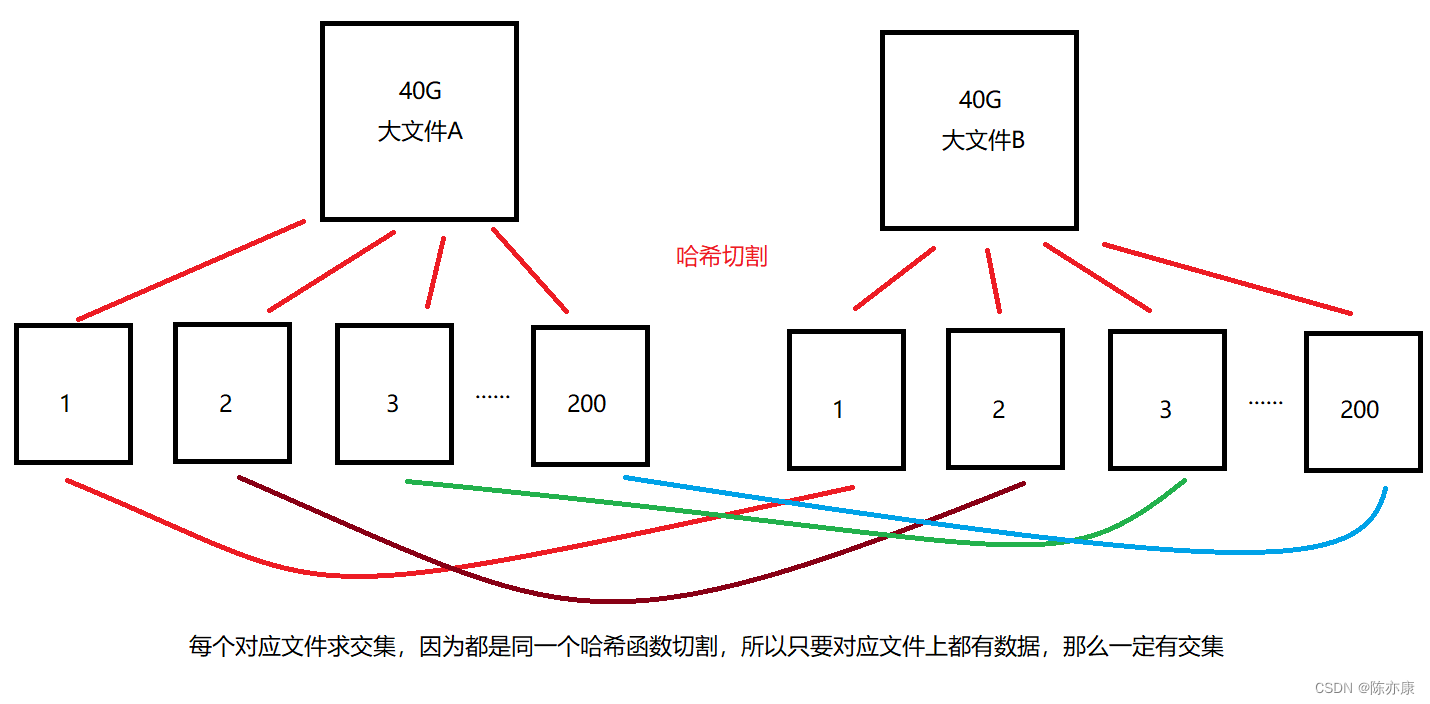
        首先，把这两个大文件都使用哈希切割分割成小文件，然后让她两分割小的文件分别对应的去求交集（哈希函数一样，若对应小文件存在数据，那么必然是交集），这样问题的就迎刃而解了，如下图：

 解法二：位图

         这个方法思路就简单多了：

        1.遍历第一个文件，将数据都读取出来放到bitSet中；

        2.再遍历第二文件，读取数据，看bitSet中是否已经存在当前读取到的数据；

        3.若存在，就是交集；

题目升华：怎么求交集？并集？差集？

思路：

        交集、并集、差集，实际上都可以用两个位图来解决，分别用两个位图去遍历存放两个文件的数据，然后进行以下操作；

问题一：交集

问题二：并集

问题三：差集

题目三

        位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

解法一：哈希切割

        这里和之前讲到的哈希切割一样，也是分成若干个小文件，通过哈希函数来映射到对应的位置，然后统计每个文件里不超过两次整数；

解法二：使用2个位图

        这里和刚刚讲到的双位图的思路是一样的，（0，0）表示没出现，（0，1）表示出现一次，（1，0）表示出现两次，（1，1）表示出现三次或以上，这道题只需要不要出现2个1的就可以，注意0次的也不要；

三、布隆过滤器

题目一

        给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和 近似算法

精确算法：哈希切割

        这里就不详细说了，上面已将讲过两次了，都是一样的方法，将两个文件分成若干小文件，再对小文件求交集；

近似算法：布隆过滤器

        使用布隆过滤器就容易很多啦，分如下两步：

        1.把第一个文件当中的query映射到布隆过滤器中；

        2.读取第2个文件，每一个query都去布隆过滤去中查找；（会存在误判）；

        注意：由于布隆过滤器只能准确判断数据一定不存在，所以，有可能会将一个没有的数据误判成了“有”；

题目二

如何扩展BloomFilter使得它支持删除元素的操作

解法一：计数器

        布隆过滤器不能直接删除数据，因为删除元素时可能会影响到其他元素；但是办法总还是有的：将布隆过滤器中的每一个bit位扩展成一个小的计数器，插入元素时给计数器加一，删除元素时给计数器减一，这是一种多占用几倍的存储空间代价来进行删除功能；

存在缺陷：

1.无法确认元素是否真正在布隆过滤器中；

2.存在计数回绕

---