目录
一、利用MATLAB进行数学模型转换
语法:
例(将传递函数写成零极点的形式):
例(将传递函数写成因子式的形式):
二、利用MATLAB求系统传递函数
串联等效:
并联等效:
反馈等效:
一、利用MATLAB进行数学模型转换
使用tf创建实值或复值传递函数模型,或转换动态系统模型传递函数形式。传递函数是线性时不变系统的频域表示。例如,考虑由传递函数表示的连续时间SISO动态系统sys(s) = N(s)/D(s),在哪里s = jw和N(s)和D(s)分别称为分子多项式和分母多项式。这tf模型对象可以表示连续时间或离散时间中SISO或MIMO传递函数。可以通过直接指定其系数或通过转换另一种类型的模型(如状态空间模型)来创建传递函数模型对象ss)转换成传递函数形式。也可以使用tf为了创建广义状态空间(genss)模型或不确定状态空间(uss(鲁棒控制工具箱))模特。
语法:
sys = tf(numerator,denominator)
sys=zpk(z,p,k);
sys = tf(numerator,denominator)创建连续时间传递函数模型,设置Numerator和Denominator属性。例如,考虑由传递函数表示的连续时间SISO动态系统sys(s) = N(s)/D(s),输入参数numerator和denominator是的系数分别为N(s)和D(s)。
sys=zpk(z,p,k)z=[ ]输入零点 ,p=[ ]输入极点;k =[ ]输入增益。
例(将传递函数写成零极点的形式):

num=[8,24,16];%分子多项式系数
den=[1,12,47,60,0];%分母多项式系数
sys=tf(num,den);
sys=zpk(sys),%转换成零极点形式输出
输出结果:

例(将传递函数写成因子式的形式):

num=[-1,-2];
den=[0,-4,-6,-25,-30];
k=10;
sys=zpk(num,den,k)%以零极点形式输出
sys1=tf(sys)%以因子式形式输出
输出结果:

二、利用MATLAB求系统传递函数
求系统串联、并联、反馈,连接方式的传递函数
串联等效:
将两个系统串联连接,串联后的传递函数可由series命令求得,其格式为:
sys=series(sys1,sys2)
[num,den]=series(num1,den1,num2,den2)
num,den(单个串联环节的分子,分母多项式系数)
例(将以下两个环节串联):


num1=[1,1];den1=[1,10];
num2=[10];den2=[1,5];
[num,den]=series(num1,den1,num2,den2);
sys1=tf(num1,den1)
sys2=tf(num2,den2)
sys=tf(num,den)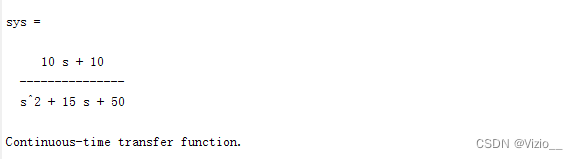
并联等效:
将两个环节并联,并联后的传递函数可由parallel命令求得,其格式为:
sys=parallel(sys1,sys2)
[num,den]=parallel(num1,den1,num2,den2)
num,den(单个串联环节的分子,分母多项式系数)
例(将以下两个环节并联):


num1=[1,1];den1=[1,10];
num2=[10];den2=[1,5];
[num,den]=parallel(num1,den1,num2,den2);
sys1=tf(num1,den1)
sys2=tf(num2,den2)
sys=tf(num,den)
反馈等效:
具有反馈连接的结构图,可以通过feedback命令求得化简后的传递函数,其格式为:
[num,den]=feedback(num1,den1,num2,den2,sign)
num,den(单个串联环节的分子,分母多项式系数)
sign为可选参数;sign=1为正反馈 sign=-1为负反馈;其默认为负反馈
例(将以下两个环节反馈连接):


num1=[1,1];den1=[1,10];
num2=[1];den2=[1,5];
[num,den]=feedback(num1,den1,num2,den2,-1);
sys1=tf(num1,den1)
sys2=tf(num2,den2)
sys=tf(num,den)
有了以上几个基本操作,可以使用MATLAB进行控制系统的结构图变换和化简