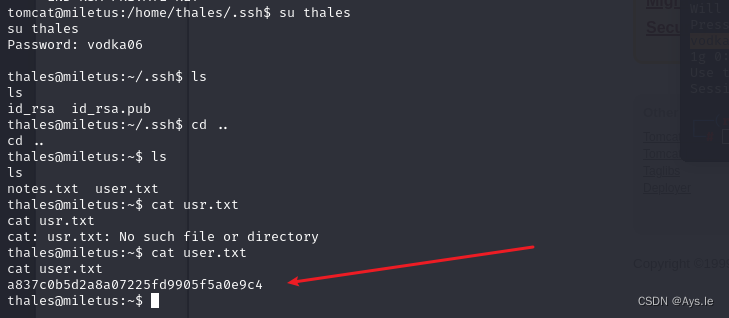
外观数列

题目描述：

「外观数列」是一个数位字符串序列，由递归公式定义：

• countAndSay(1) = "1"
• countAndSay(n) 是 countAndSay(n-1) 的行程长度编码。

行程长度编码（RLE）是一种字符串压缩方法，其工作原理是通过将连续相同字符（重复两次或更多次）替换为字符重复次数（运行长度）和字符的串联。例如，要压缩字符串 "3322251" ，我们将 "33" 用 "23" 替换，将 "222" 用 "32" 替换，将 "5" 用 "15" 替换并将 "1" 用 "11" 替换。因此压缩后字符串变为 "23321511"。

给定一个整数 n ，返回 外观数列 的第 n 个元素。

示例 1：

输入：n = 4

输出："1211"

解释：

countAndSay(1) = "1"

countAndSay(2) = "1" 的行程长度编码 = "11"

countAndSay(3) = "11" 的行程长度编码 = "21"

countAndSay(4) = "21" 的行程长度编码 = "1211"

示例 2：

输入：n = 1

输出："1"

解释：

这是基本情况。

提示：

• 1 <= n <= 30

思路分析：

        根据题意进行模拟，从起始条件 k=1 时 ans = "1" 出发，逐步递推到 k=n 的情况，对于第 k 项而言，其实就是对第 k−1项的「连续段」的描述，而求「连续段」长度，可以使用双指针实现。

代码实现注解：

class Solution {
    public String countAndSay(int n) {
        //设ans的初始值为1
        String ans = "1";
        for(int i= 2; i<=n;i++){
            //cur用来存放当前连续段
            String cur = "";
            //len为前一个连续段的长度
            int len = ans.length();
            //遍历前一个连续段得到当前描述
            for(int j = 0;j<len; ){
                //k指向当前遍历位置
                int k = j+1;
                //判断前后两数是否相同，相同则累加
                while(k<len && ans.charAt(j) == ans.charAt(k))
                    k++;
                //cnt用来记录重复数的个数
                int cnt = k-j;
                //拼接得到cur
                cur += cnt + "" + ans.charAt(j);
                //将j移动到当前遍历位置
                j = k;
            }
            ans = cur;
        }
        return ans;
    }
}