目录
- A. World Final? World Cup! (I)
- 思路
- B. World Final? World Cup! (II)
- C. 现在是,学术时间 (I)
- 思路
- D. 现在是,学术时间 (II)
- 思路
- E. 鸡算几何
- 思路
- F. 鸡玩炸蛋人
- 思路
- G. 鸡格线
- 思路
- H. 本题主要考察了DFS
- 思路
- I. 本题也主要考察了DFS
- J. 本题竟也主要考察了DFS
- K. 本题主要考察了dp
- 思路
- L. 本题主要考察了运气
- 思路
- M. 本题主要考察了找规律
- 思路
A. World Final? World Cup! (I)
思路
tag:枚举
暴力枚举,判断当前剩余场次是否足够翻盘,如果满足则继续枚举,不满足则直接break输出当前场次
void solve()
{
string s;
cin>>s;
s='#'+s;
int n=10;
int a=0,b=0;
rep(i,1,n)
{
if(i%2)
{
if(s[i]=='1')a++;
}
else
{
if(s[i]=='1')b++;
}
int x=0,y=0;
rep(j,i+1,n)
if(j%2)x++;
else y++;
if(a>b+y)
{
cout<<i<<endl;
return;
}
if(b>a+x)
{
cout<<i<<endl;
return;
}
}
if(a==b)cout<<-1<<endl;
}
B. World Final? World Cup! (II)
待补。。。
C. 现在是,学术时间 (I)
思路
tag:思维,诈骗
至少H篇论文的引用大于等于H,所以一篇论文最大贡献也是1,考虑论文数和人数一样,每个人分配一篇论文就好了,记录0的个数。
int n;
const int N=1e5+10;
int a[N];
void solve()
{
int s=0;
cin>>n;
rep(i,1,n)cin>>a[i],s+=a[i]==0;
cout<<n-s<<endl;
}
D. 现在是,学术时间 (II)
思路
tag:几何计算,暴力
我写的比较麻烦,分成了九个部分分别枚举不同情况求解,分子分母同时加一个数越接近整数1,所以尽可能选取大的面积,求出来的IOU就尽可能大。数学证明就不证了。
void solve()
{
int x,y,xp,yp;
scanf("%lld%lld%lld%lld",&x,&y,&xp,&yp);
lb res=0;
int maxx=0,maxy=0;
if(xp>=0&&xp<=x&&yp>=0&&yp<=y)
{
maxx=max(xp,abs(x-xp));
maxy=max(yp,abs(y-yp));
res=maxx*maxy*1.0/(x*y);
}
else if(xp>x&&yp<=y&&yp>=0)
{
maxx=xp;
maxy=max(abs(0-yp),abs(y-yp));
lb area1=x*maxy;
lb area2=x*y+(xp-x)*maxy;
res=area1/area2;
}
else if(xp>x&&yp>y)
{
maxx=xp;
maxy=yp;
lb area1=x*y;
lb area2=xp*yp;
res=area1/area2;
}
else if(xp>x&&yp<0)
{
maxx=xp;
maxy=y-yp;
lb area1=x*y;
lb area2=maxx*maxy;
res=area1/area2;
}
else if(xp<0&&yp<=y&&yp>=0)
{
maxx=x-xp;
maxy=max(abs(0-yp),abs(y-yp));
lb area1=x*maxy;
lb area2=x*y+(-xp*maxy);
res=area1/area2;
}
else if(xp<0&&yp>y)
{
maxx=x-xp;
maxy=yp;
lb area1=x*y;
lb area2=maxx*maxy;
res=area1/area2;
}
else if(xp<0&&yp<y)
{
maxx=x-xp;
maxy=y-yp;
lb area1=x*y;
lb area2=maxx*maxy;
res=area1/area2;
}
else if(xp>=0&&xp<=x&&yp<0)
{
maxx=max(xp,abs(x-xp));
maxy=-yp+y;
lb area1=maxx*y;
lb area2=x*y+(maxx*(-yp));
res=area1/area2;
}
else if(xp>=0&&xp<=x&&yp>0)
{
maxx=max(xp,abs(x-xp));
maxy=yp;
lb area1=y*maxx;
lb area2=x*y+maxx*(yp-y);
res=area1/area2;
}
printf("%.9Lf\n",res);
}
E. 鸡算几何
思路
tag:几何,to_left
判断是否进行了反转操作,判断叉积的正负。
几何意义:向量A与B张成的平行四边形的有向面积。B在A的逆时针方向为正。
求出两个斜边的叉积判断正负符号是否相同即可。
double len(PDD a)
{
return a.x*a.x+a.y*a.y;
}
double to_left(PDD a,PDD b)
{
return a.x*b.y-a.y*b.x;
}
PDD a,b,c,d,e,f;
PII ba,bc;
PDD ed,ef;
void solve()
{
cin>>a.x>>a.y>>b.x>>b.y>>c.x>>c.y;
cin>>d.x>>d.y>>e.x>>e.y>>f.x>>f.y;
ba={a.x-b.x,a.y-b.y},bc={c.x-b.x,c.y-b.y};
if(len(ba)==len(bc))
{
NO;
return;
}
ed={d.x-e.x,d.y-e.y},ef={f.x-e.x,f.y-e.y};
if(fabs(len(ed)-len(bc))<eps)swap(ba,bc);
int c1=to_left(ba,bc);
double c2=to_left(ed,ef);
if(c1*c2<0)YES;
else NO;
}
F. 鸡玩炸蛋人
思路
tag:并查集,思维,诈骗
如果整个地图没有炸弹,那么每个连通块的每个点都可以取起点和终点,则ans=
∑
i
=
1
s
u
m
连通块
\sum_{i=1}^{sum_{连通块}}
∑i=1sum连通块
c
n
t
i
∗
c
n
t
i
cnt_i*cnt_i
cnti∗cnti。
如果地图有炸弹,如果所有炸弹都在连通块
x
x
x内,则ans=
c
n
t
x
∗
c
n
t
x
cnt_x*cnt_x
cntx∗cntx。
否则不存在,因为图并不联通,所以没有办法全部下蛋。
int n,m;
const int N=2e5+10;
int f[N],cnt[N],s[N];
int find(int x)
{
if(x!=f[x])f[x]=find(f[x]);
return f[x];
}
void unite(int a,int b)
{
a=find(a),b=find(b);
if(a!=b)
{
f[b]=a;
cnt[a]+=cnt[b];
s[a]+=s[b];
}
}
void solve()
{
cin>>n>>m;
rep(i,1,n)f[i]=i,cnt[i]=1;
vector<PII>v;
rep(i,1,m)
{
int a,b;
cin>>a>>b;
v.pb({a,b});
}
int sum=0;
rep(i,1,n)cin>>s[i],sum+=s[i];
rep(i,0,m-1)
unite(v[i].x,v[i].y);
int res=0;
if(sum==0)
{
rep(i,1,n)
if(find(i)==i)
res+=cnt[i]*cnt[i];
}
else
{
rep(i,1,n)
if(find(i)==i)
if(s[i]==sum)
{
res=cnt[i]*cnt[i];
break;
}
}
cout<<res<<endl;
}
G. 鸡格线
思路
tag:STL+打表找规律
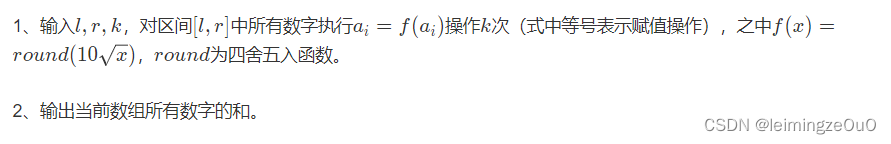
这题难在发现规律,打表不难发现,该数列分别收敛于0,99,100
那么做法就有很多了,我写了线段树和mp+二分的写法。
int n,m;
const int N=1e5+10;
int a[N];
struct node
{
int l,r;
int sum;
bool f;
}tr[4*N];
void up(int u)
{
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
tr[u].f=tr[u<<1].f&tr[u<<1|1].f;
}
void build(int u,int l,int r)
{
tr[u]={l,r};
if(l==r)
{
tr[u].sum=a[l];
return;
}
int mid=tr[u].l+tr[u].r>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
up(u);
}
void modify(int u,int l,int r,int k)
{
if(tr[u].f)return;
if(tr[u].l==tr[u].r)
{
for(int i=1;i<=k;i++)
{
int t=tr[u].sum;
tr[u].sum=round(10*sqrtl(tr[u].sum));
if(t==tr[u].sum)
{
tr[u].f=true;
break;
}
}
}
else
{
int mid=tr[u].l+tr[u].r>>1;
if(l<=mid)modify(u<<1,l,r,k);
if(r>mid)modify(u<<1|1,l,r,k);
up(u);
}
}
void solve()
{
cin>>n>>m;
rep(i,1,n)cin>>a[i];
build(1,1,n);
rep(i,1,m)
{
int op;cin>>op;
if(op==1)
{
int l,r,k;
cin>>l>>r>>k;
modify(1,l,r,k);
}
else cout<<tr[1].sum<<endl;
}
}
int n,m;
const int N=1e5+10;
int a[N];
map<int,int>mp;
void solve()
{
cin>>n>>m;
int res=0;
rep(i,1,n)cin>>a[i],res+=a[i],mp[i]=a[i];
mp[-1]=1,mp[n+1]=1;
rep(i,1,m)
{
int op;cin>>op;
if(op==2)cout<<res<<endl;
else
{
int l,r,k;
cin>>l>>r>>k;
for(auto it=mp.lower_bound(l);it->x<=r;it++)
{
int x=it->x,&y=it->y;
for(int j=1;j<=k;j++)
{
int m=round(10*sqrtl(y));
res-=y;
res+=m;
if(y==m)
{
it=mp.erase(it);
it--;
break;
}
y=m;
}
}
}
}
}
H. 本题主要考察了DFS
思路
tag:思维,诈骗
多一块权值+1,少一块权值-1,所以直接用总面积减去已知面积即可。
int n;
void solve()
{
cin>>n;
string s;
int res=n*n*10;
rep(i,1,n*n-1)
{
cin>>s;
int sum=10;
rep(j,0,3)
{
if(s[j]=='1')sum--;
else if(s[j]=='2')sum++;
}
//cout<<sum<<endl;
res-=sum;
}
cout<<res<<endl;
}
I. 本题也主要考察了DFS
待补。。。
J. 本题竟也主要考察了DFS
待补。。。
K. 本题主要考察了dp
思路
tag:贪心,构造
凑出尽可能多的一个1两个0的子串,尽量让第一个1处于最左端,否则会浪费0,所以构造出100100111这种构造方案,然后暴力check即可
int n,m;
void solve()
{
cin>>n>>m;
int zero=n-m,one=m;
vector<int>v;
rep(i,1,n)
{
if(one)
{
int k=0;
v.pb(1);one--;
while(k<2&&zero)zero--,v.pb(0),k++;
}
}
int res=0;
for(int i=0;i+2<n;i++)
{
int j=i+2;
int a=0,b=0;
for(int k=i;k<=min(n-1,j);k++)
if(v[k]==0)a++;
else b++;
if(b>a)res++;
}
cout<<res<<endl;
}
L. 本题主要考察了运气
思路
并没有思路(太菜了不会),从1到100试试运气把。
void solve()
{
cout<<32<<endl;
}
M. 本题主要考察了找规律
思路
tag: dp
和背包差不多,多了每次枚举当前给了多少仙贝。
int n,m;
const int N=510;
lb f[N][N];
void solve()
{
scanf("%lld%lld",&n,&m);
rep(i,1,m)f[1][i]=1.0*i/m;
rep(i,2,n)
{
rep(j,1,m)
{
rep(k,1,j)
{
f[i][j]=max(f[i][j],f[i-1][j-k]+1.0*k/(m-j+k));
}
}
}
lb res=0;
rep(i,1,m)res=max(res,f[n][i]);
printf("%.8Lf",res);
}



![[ROS2 入门] rqt_console 使用介绍](https://img-blog.csdnimg.cn/img_convert/c0b4a5e8372ea22d466c05937e096a36.png)