【资源限制】
内存限制:256.0MB C/C++时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s
【问题描述】
对于一棵多叉树,我们可以通过 “左孩子右兄弟” 表示法,将其转化成一棵二叉树。
如果我们认为每个结点的子结点是无序的,那么得到的二叉树可能不唯一。换句话说,每个结点可以选任意子结点作为左孩子,并按任意顺序连接右兄弟。
给定一棵包含 N 个结点的多叉树,结点从 1 至 N 编号,其中 1 号结点是根,每个结点的父结点的编号比自己的编号小。请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树,高度最高是多少。
注:只有根结点这一个结点的树高度为 0。
例如如下的多叉树:
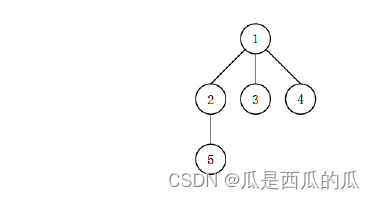
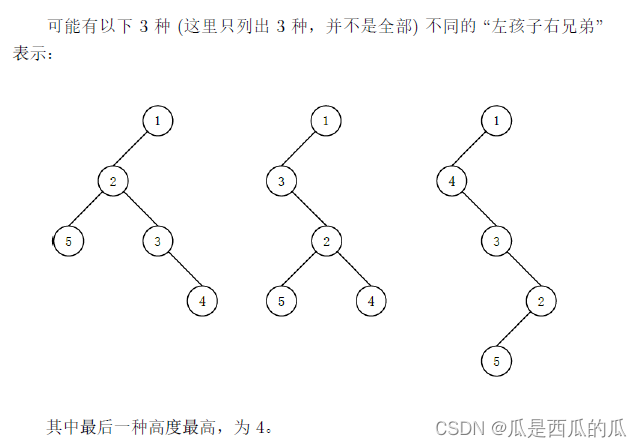
【输入格式】
输入的第一行包含一个整数 N。
以下 N−1 行,每行包含一个整数,依次表示 2 至 N 号结点的父结点编号。
【输出格式】
输出一个整数表示答案。
【样例输入】
5
1
1
1
2
【样例输出】
4
【评测用例规模与约定】
对于 30% 的评测用例,1≤N≤20;
对于所有评测用例,1≤N≤100000。
【基础知识要求】
首先要知道何为“左孩子右兄弟”表示法,不然这个题是要直接pass的。
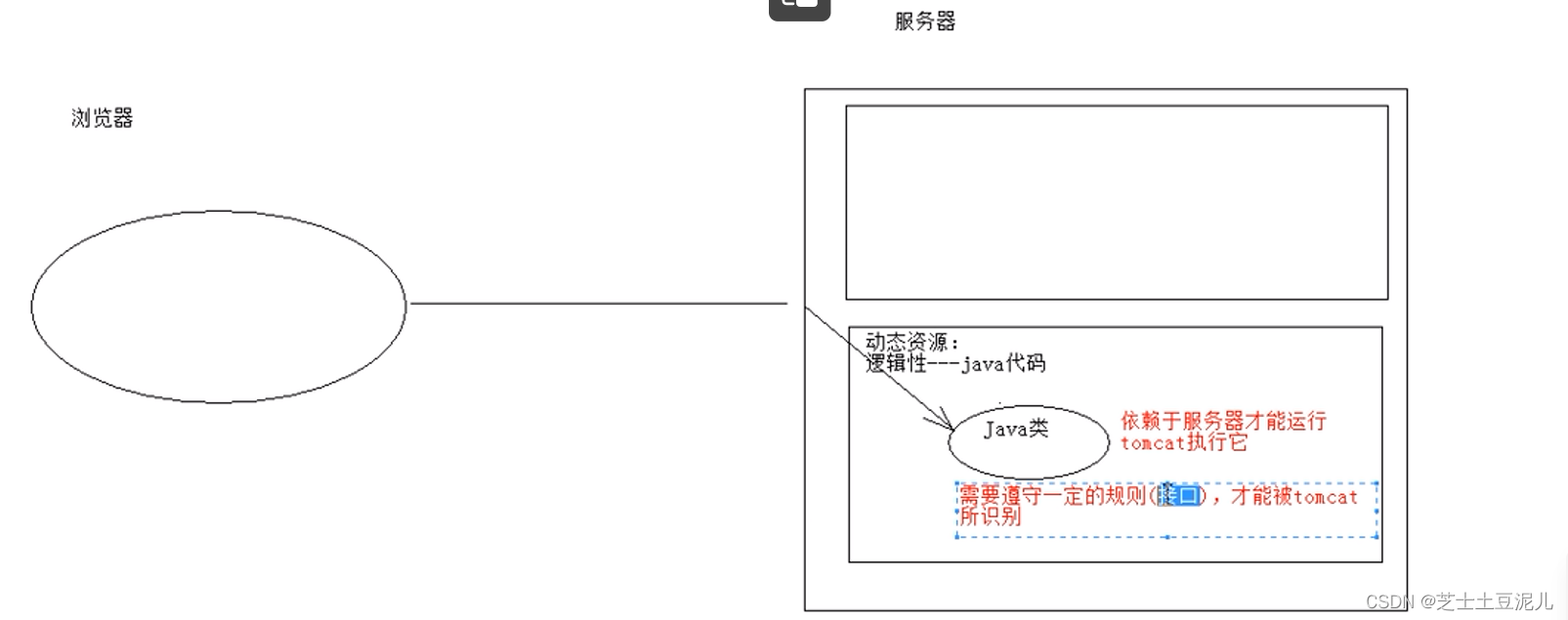
何为“左孩子右兄弟”表示法?
答:大家都知道,在树结构中,同一层的节点互为兄弟节点。上层与下层相连的节点为父子节点。那么,所谓的“孩子兄弟表示法”,指的是用将整棵树用二叉链表存储起来,从树的根节点开始,依次存储各个结点的孩子结点和兄弟结点。
因此,各个节点又包含了三部分内容:
1.节点的值;
2.指向孩子结点的指针;
3.指向兄弟结点的指针;

而通过孩子兄弟表示法,任意一棵普通树都可以相应转化为一棵二叉树,它们之间是一一对应的。因此,孩子兄弟表示法可以作为将普通树转化为二叉树的最有效方法,通常又被称为"二叉树表示法"或"二叉链表表示法"。
【思路与分析】
从根节点向下看,当前节点的最深深度 = 当前节点的子节点(一个在左,其他的节点都在右侧。因为左孩子右兄弟的原则) + 所有子节点距离当前子节点的最深深度。也就是说,树的最大高度=父节点孩子的数目+以它的孩子为父节点的子树的最大高度。
同样,题内有一个细节需要我们注意:根结点这一个结点的树高度为 0。
【代码】
import java.util.*;
public class Main {
//声明一个数据类型,模拟二叉树
public static Map<Integer,ArrayList<Integer>> erTree = new HashMap<>();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//使用Integer这一包装类而不使用int的原因为:Integer是对象,int仅表示值
Integer n = sc.nextInt();
for(int i = 2; i <= n; i++) {
Integer fa = sc.nextInt();
//判断是否存在该父节点,没有则添加
if(!erTree.containsKey(fa)) {
ArrayList<Integer> list = new ArrayList<>();
erTree.put(fa,list);
}
erTree.get(fa).add(i);
}
System.out.println(shen(1));
}
public static int shen(int n) {
//通过判断舍弃无效数据,优化运算量
if(!erTree.containsKey(n)) {
return 0;
}
//获得子树
ArrayList<Integer> list = erTree.get(n);
//获得以1为父节点的孩子节点的数目
int size = list.size();
int max = 0;
//遍历子树,获得以n为父节点的子树的最大高度
for(Integer i : list) {
max = Math.max(max,shen(i));
}
return size + max;
}
}