目录
什么是扫描线算法?
扫描线简单应用
更多的扫描线
什么是扫描线算法?
在计算几何中,扫描线算法(scan line algorithm)一般用来解决几何图形的面积交并,周长交并问题,扫描线算法的核心思想是利用扫描线(通常是水平线或垂直线)在几何空间中“扫描”对象,以确定哪些对象与扫描线相交。
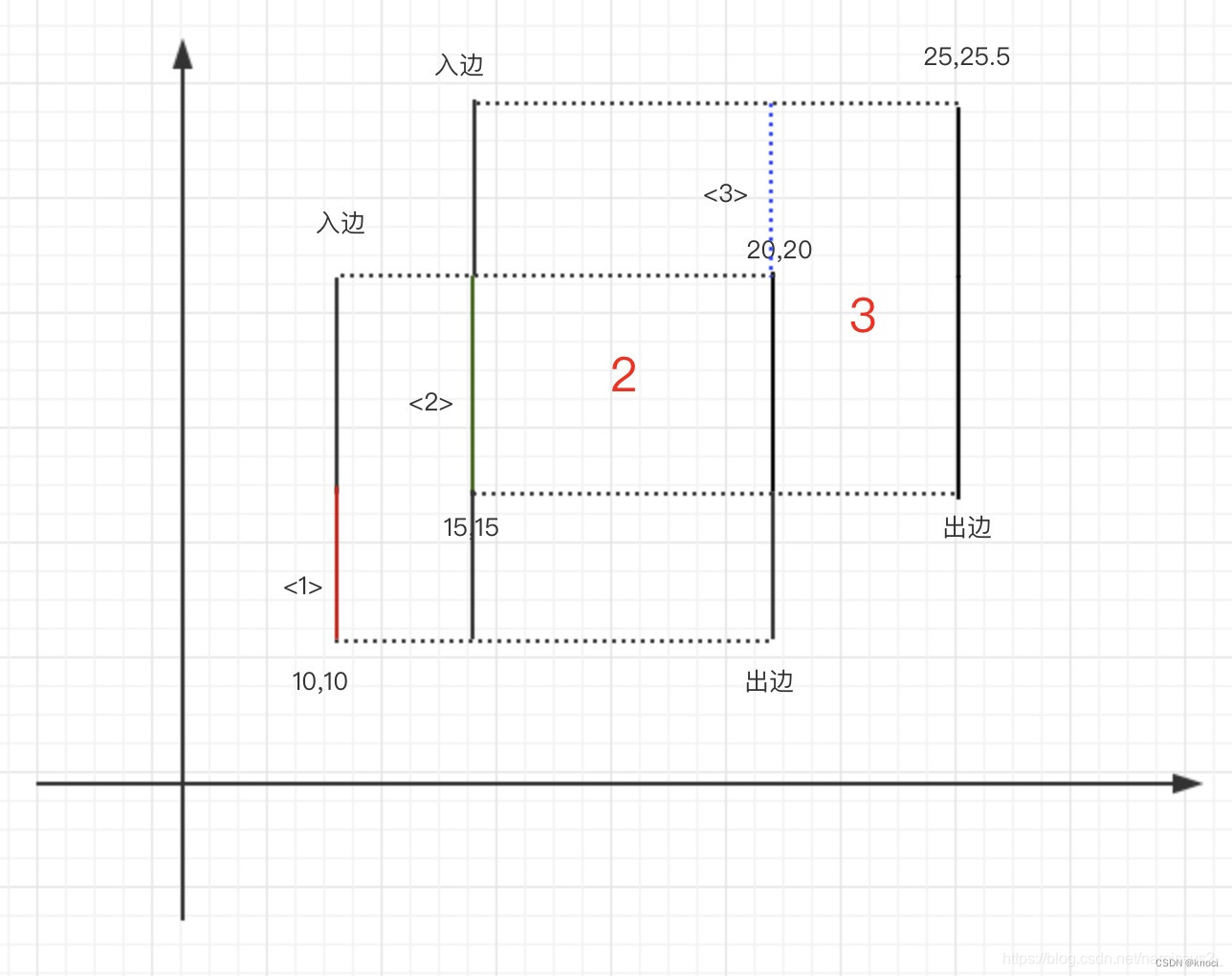
下面我们就来通过求矩形的面积并来介绍扫描线算法。先来看看怎么求下面图形的面积并:
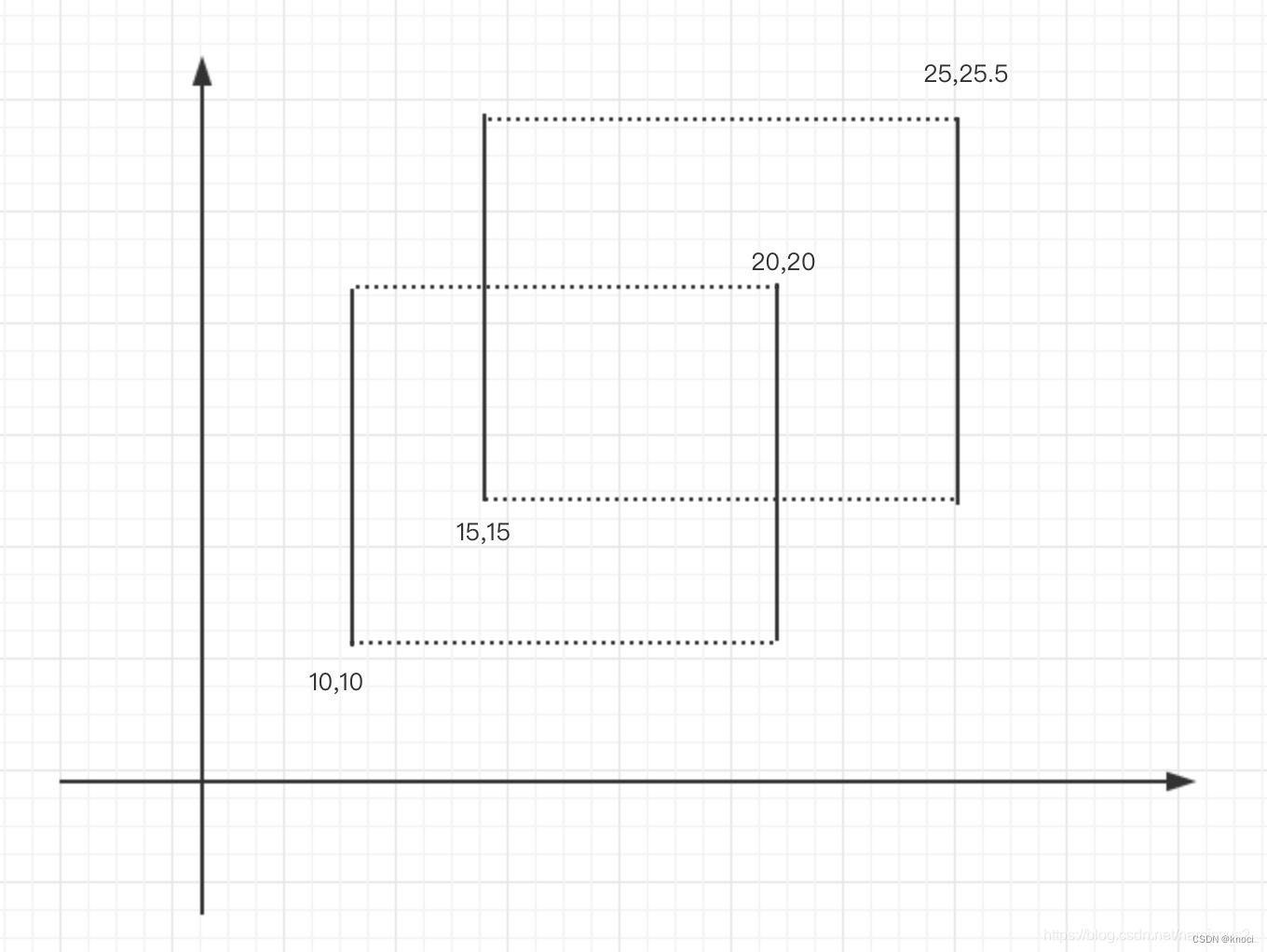
传统算法是两个矩形面积相加减去重合的面积:
(20−10)∗(20−10)+(25−15)∗(25.5−15)−(20−15)∗(20−15)=180.0
但是这样算非常的耗费时间,因为每个矩形都需要两两配对,查看互相之间是否有交集。
那么我们接下来就想着把矩形分成三部分:
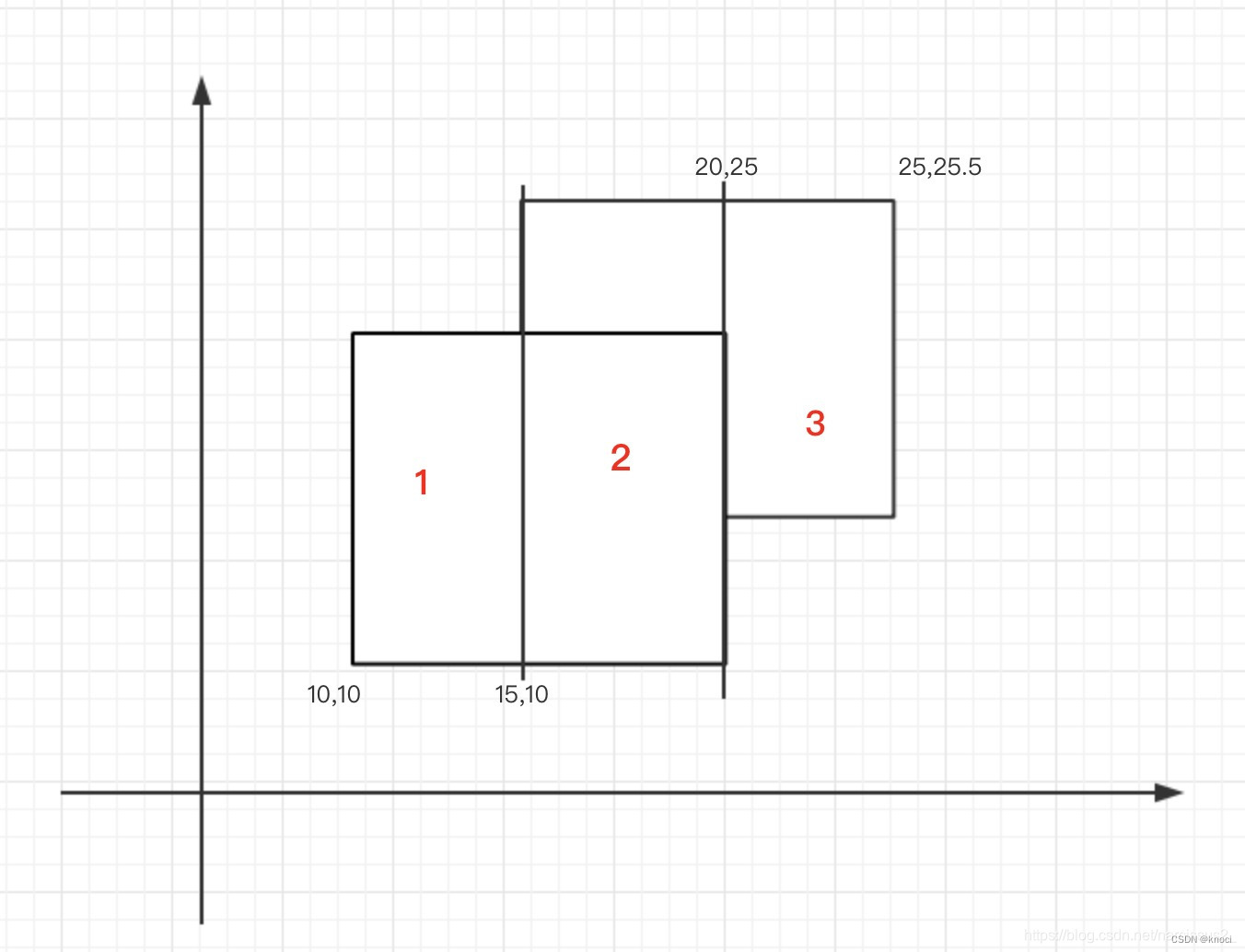
于是现在就变成了
( 20 − 10 ) ∗ ( 15 − 10 ) + ( 25.5 − 10 ) ∗ ( 20 − 15 ) + ( 25.5 − 15 ) ∗ ( 25 − 20 ) = 180
采取这个方法的好处就是只需要从左往右扫,一步一更新即可,而这个从左往右,或者从下往上扫的思想就是扫描线。
扫描线简单应用
我们看看上面的图,显然,计算面积需要两个信息
- 每个新矩形的的高度。
- 每个新矩形的宽度。
那么我们先从计算宽度说起,其实计算宽度很简单。我们把垂直于x的边单独挑出来然后按照x的大小排个序,隔位相减就可以得到。如kuan[0] = 15 - 10; kuan[1] = 20 -15;......
然后来计算矩形的高度,这是整个扫描线最难理解的地方。
首先思考一个问题:为什么二号矩形的高是(10+(25.5−10))呢?很直观的回答就是:那是因为得算上1号矩形高,再加上2号矩形多出来的部分
那为什么三号矩形的高是(25.5−5)呢?那是因为得用2号矩形的高那部分减去,减掉2号矩形下面多出来的部分
那为什么有时候“多出来”是加上一个值,有时候“多出来”是减掉一个值呢?这个问题其实也是得到高度最核心的问题,就是“入边”和“出边”的问题。
定义:在同一个矩形内,从左往右看,第一条看到的边为“入边”,第二条看到的边为“出边”其实所谓的从左往右(也可以是从上往下),就是扫描线的方向。当从左往右扫,遇到入边的线,则对入边区间扫到进行+1操作,遇到出边,那么对出边区间进行-1操作,这样子就可以解释“有时候“多出来”是加上一个值,有时候“多出来”是减掉一个值”这个问题了
凭借这个知识,我们来思考步骤
- 第一条为入边,区间为[10,20],则区间[10,20] +1(此时区间[10,20] = 1)
- 查看整个域的区间,只有[10,20]有值,则Kuan[0]*10 = 50
- 第二条边为入边,区间为[15,25.5],则[15,25.5]+1(此时区间[10,15]=1,[15,20]=2,[20,25.5]=1)
- 查看整个域区间,从[10,25.5]有值,则Kuan[1]*(25.5-10) = 77.5
- 第三条边为出边,区间从[10,20],则[10,20]-1(此时区间为[15,25.5] = 1)
- 查看整个区间,从[15,25.5]有值,则Kuan[2]*(25.5-15) = 52.5
- 第四条边为出边,区间从[15,25.5],此时-1,区间值变为0
- 区间无值,遍历结束。
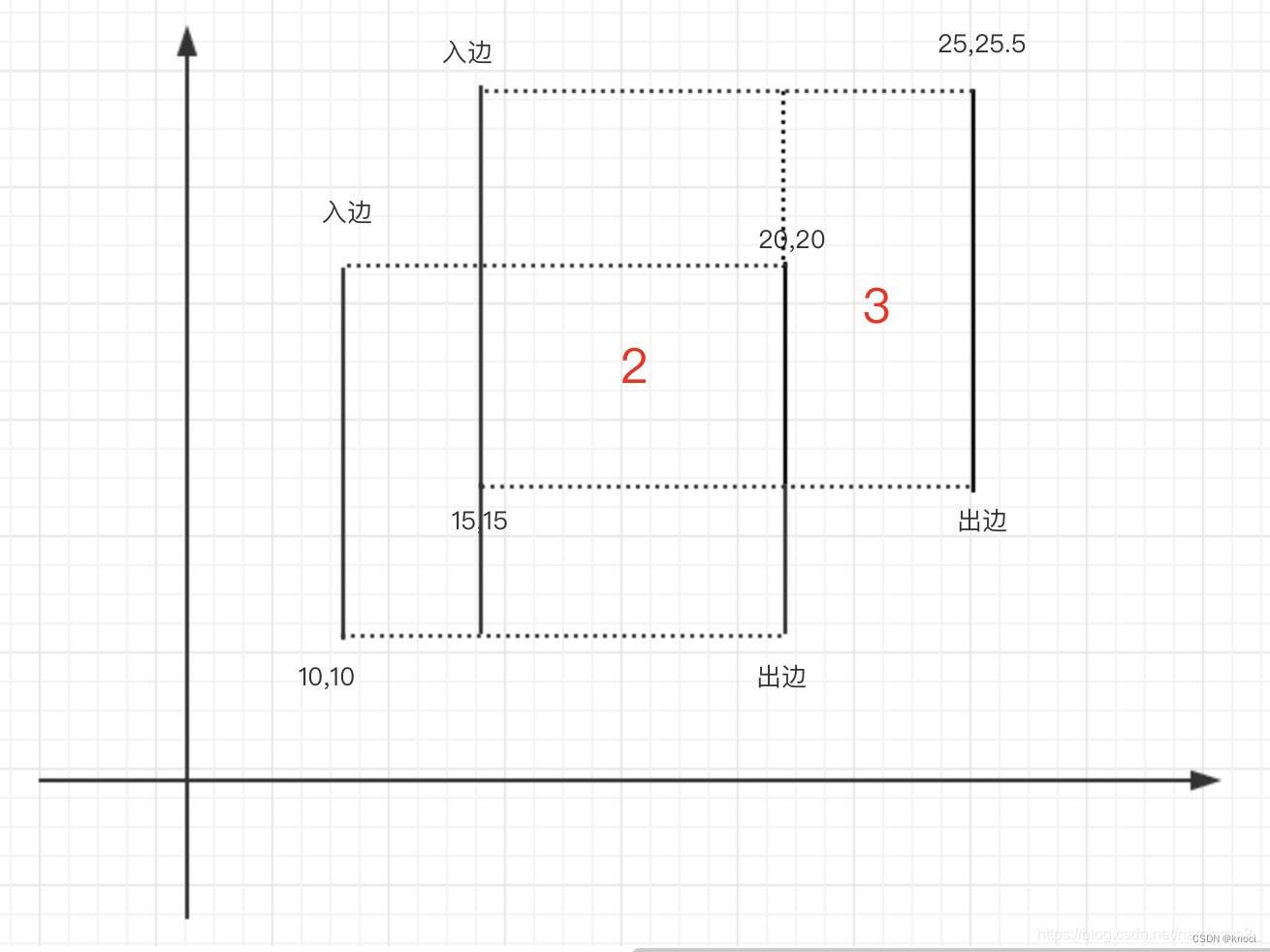
这时候问题就来了,总所周知,下标可存不了25.5,而且它这个区间要是特别大,数组会存不下。这时候就可以用离散化来存放下标。
我们把y坐标离散化用一个区间数组记录每个区间的值:于是现在[10,15]成为块1,[15,20]成为块2,[20,25.5]成为块3。则现在更新第一条入边[10,20]就变成更新[1,3],更新第二条边就变成更新[2,4],之后再查表全部乘起来即可。
建立一个线段树,用一个cover表示区间[left,right]被覆盖的次数,用len表示这个区间的合法长度,那query(1到n)的合法长度,自然就能返回总共的区间长度了。
int cover[maxn];//存放i节点对应覆盖情况的值
double length[maxn];//存放区间i下的总长度
double yy[maxn];//存放离散后的y值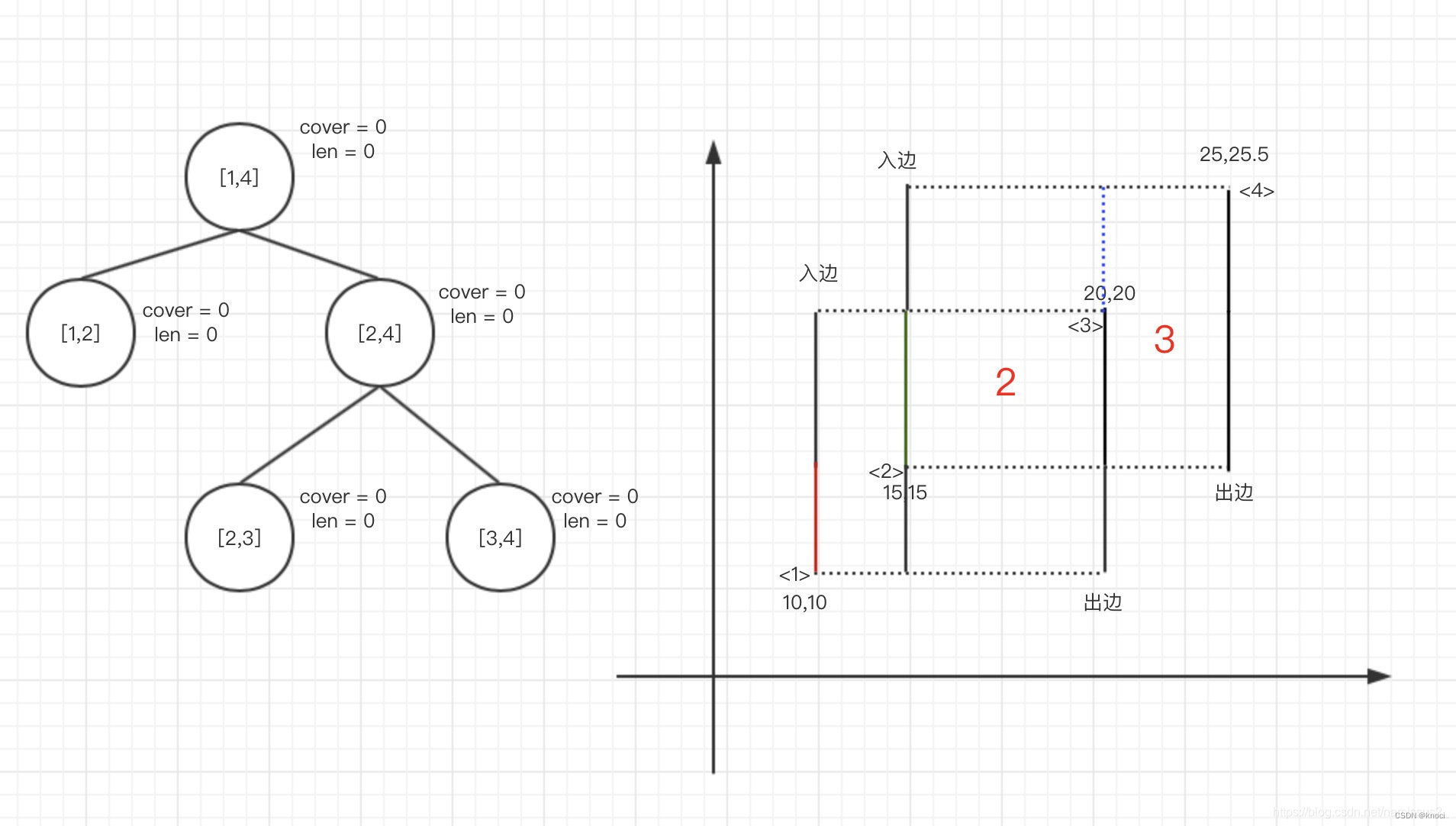
仔细观察,这棵树似乎和之前的线段树不一样,它的叶子节点的[l,r]不相等,而是差别为1。
这是因为点对于求面积的题目毫无意义,我们最需要的是它每一个基础的“块”。
1.第一条为入边,区间为[1,3],则区间cover[1,3] +1(此时区间[1,3] = 1)
2.query整个域的区间,得到len=10,则sum += Kuan[0]*10 = 50,消去len
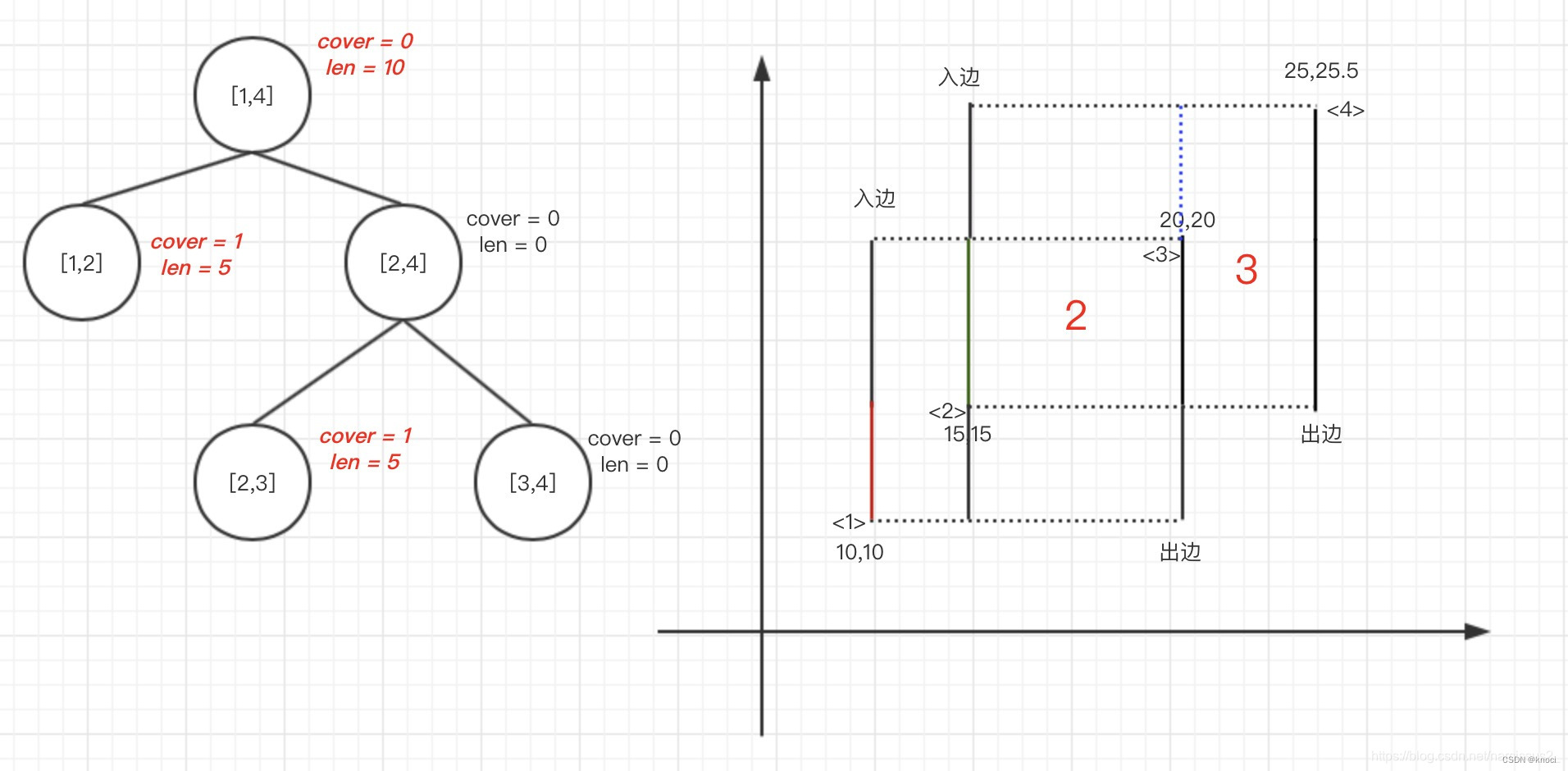
3.第二条边为入边,区间为[2,4],则cover[2,4]+1(注意:这里只需要上推len,不需要下推cover至[2,3]和[3,4],也不需要上推cover至[1,4]。只要找到对应结点的区间能完全覆盖当前线段区间就可以回溯统计了,并不需要更新到叶子节点,这是线段树为什么效率高的原因)
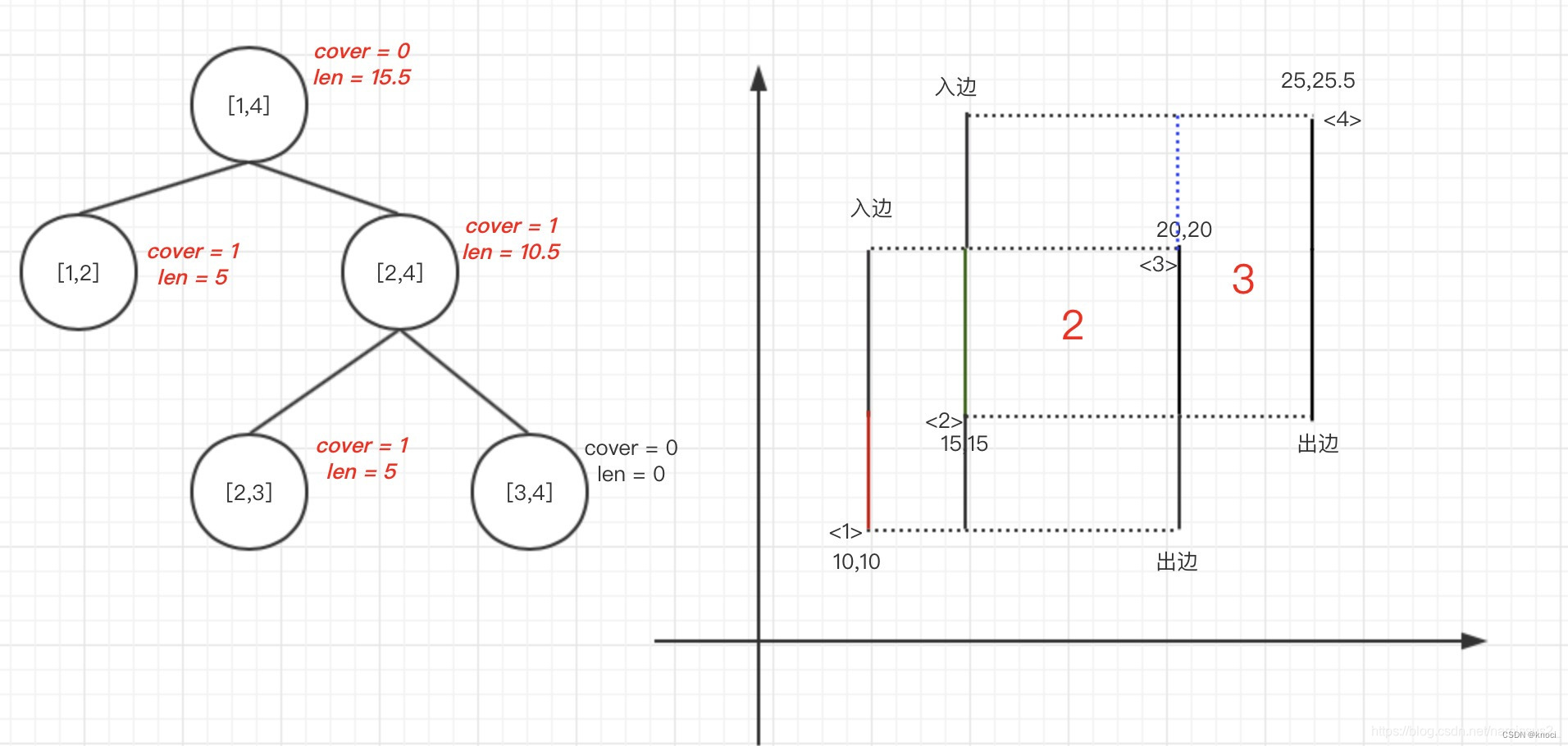
4.query整个区间,得到len = 15.5,则sum += Kuan[1]*(25.5-10) = 77.5,消去len
5.第三条边为出边,区间从[1,3],则[1,3]-1
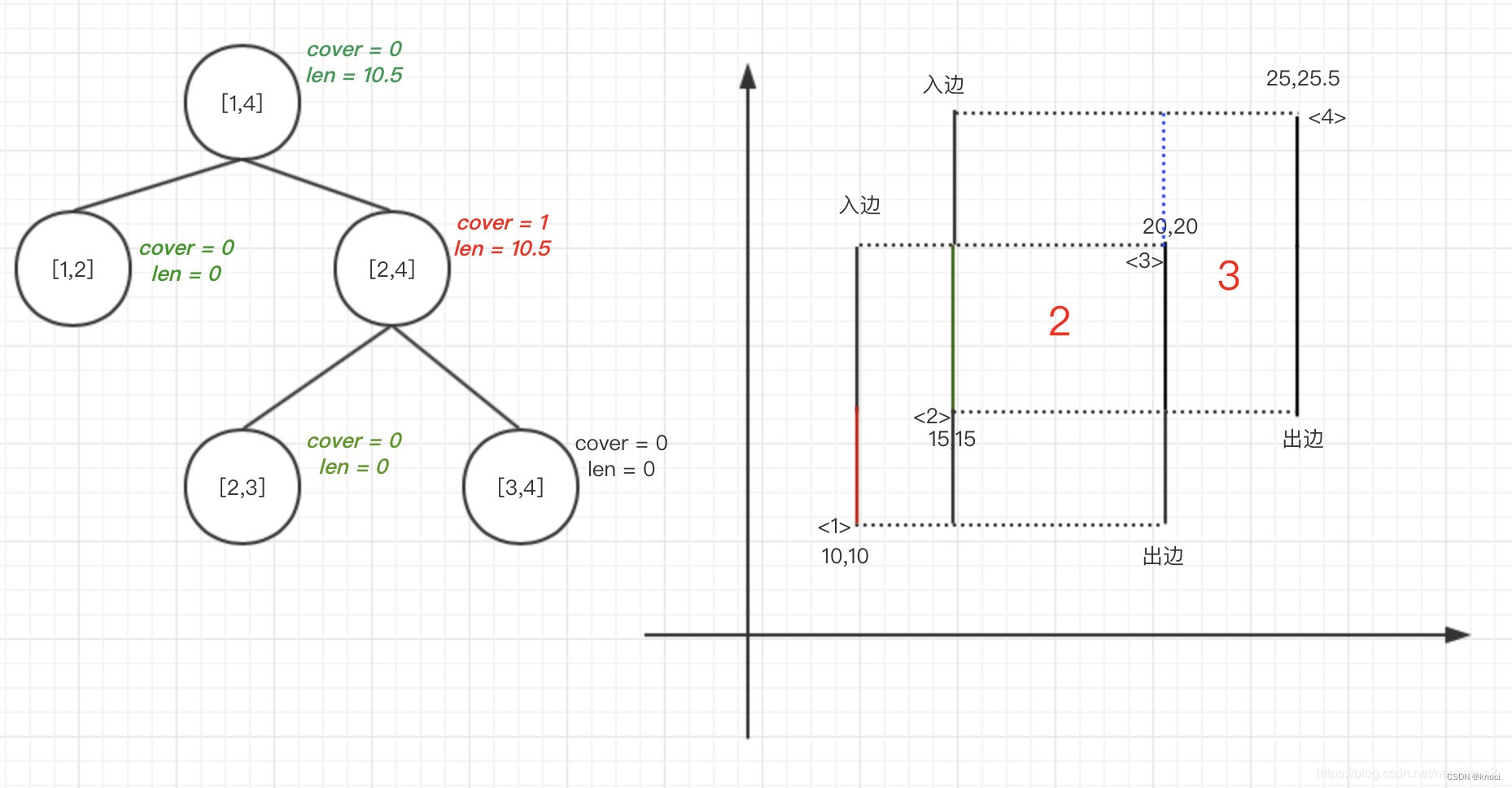
6.query整个区间,得到10.5,则sum += Kuan[2]*10.5 = 52.5,消去len
7.第四条边为出边,区间从[15,25.5],此时-1,整个区间没掉
8.query整个区间,值为0,遍历结束。
此时sum = 50 + 77.5 + 52.5 = 180,答案正确,这就是线段树用来解决矩形面积并的基本思路了。
更多的扫描线
除了矩形,三角形,梯形,圆这些几何图形的面积并也可以用扫描线求出。因为扫描线算法的思想其实接近于微积分,即求出每个单位内的微分作积,而求任何几何图形的面积,在数学里我们使用的最多的就是微积分的方法,计算几何中,我们也常常使用自适应辛普森积分公式,格林公式等微积分的方法来求相关值,所以扫描线算法这种模拟微分也是可以的,并且精度方面占点优势:
等腰三角形的扫描线模型:
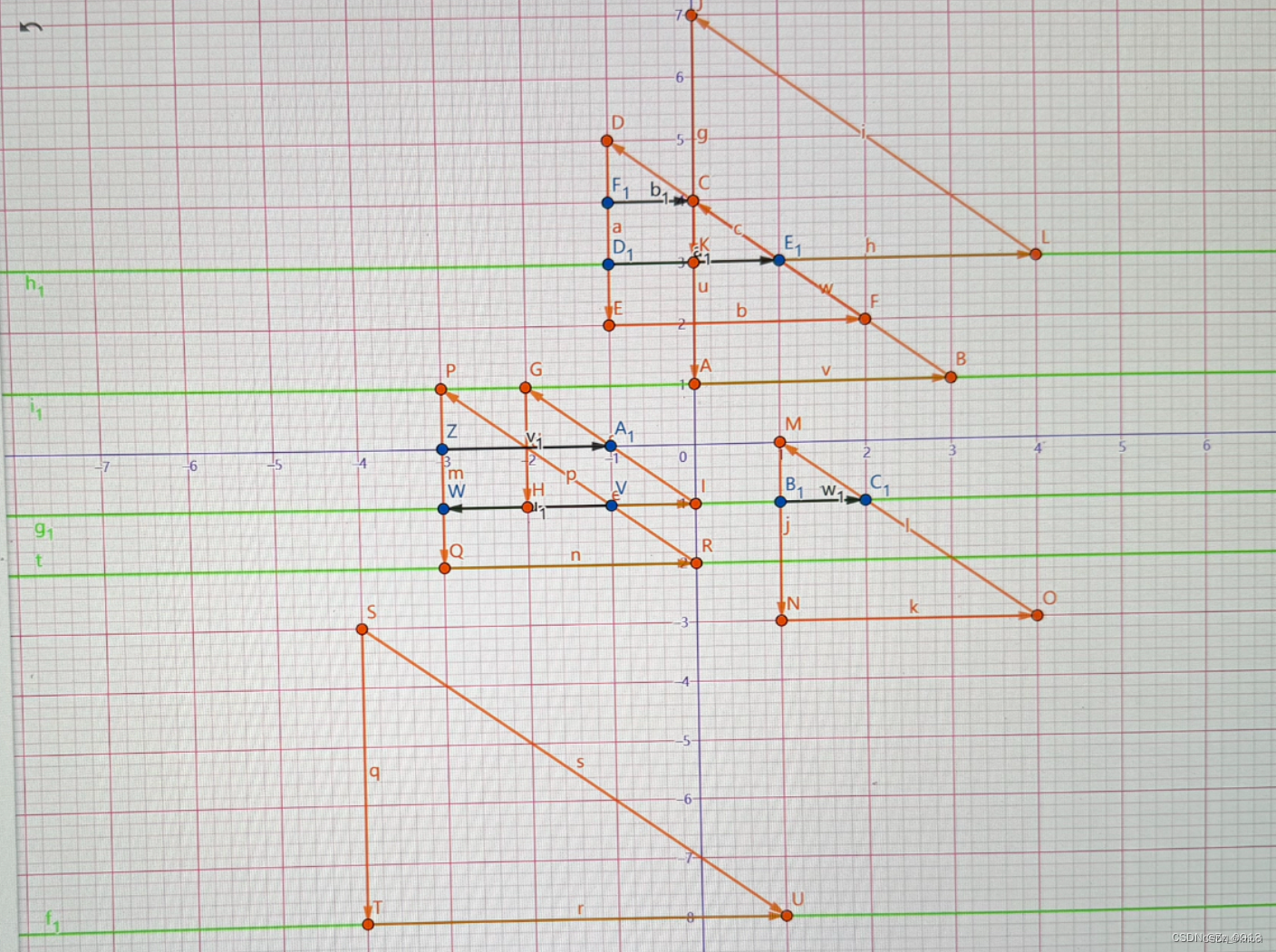
圆离散后的扫描线模型:
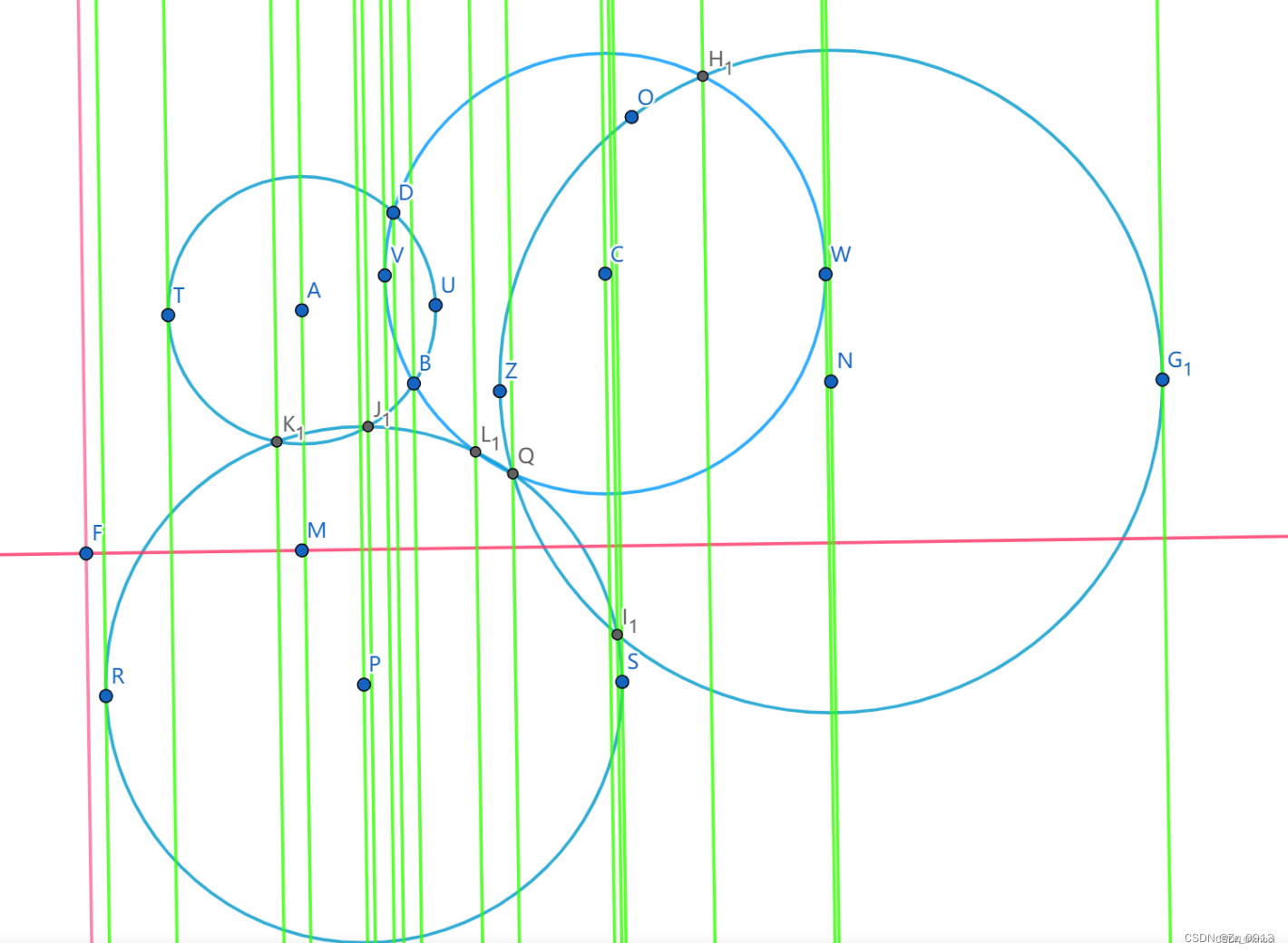
辛普森公式:

格林公式:

辛普森积分: