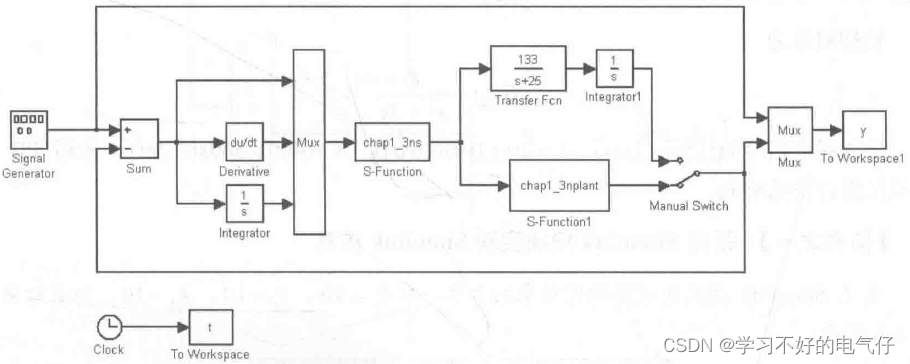
利用简化S函数，实现连续系统PID的Simulink仿真-2中S函数同样的功能。

利用S函数简化形式实现被控对象的表达、控制器的设计及仿真结果的输出。在简化S函数中，flag-0时为S函数初始化，其中 sys包括6个参数:第1个参数表示连续系统的阶数;第2个参数表示离散系统的阶数;第3个参数表示S函数的输出个数;第4个参数表示S函数的输入个数;第5个参数表示直接馈通(DirFeedthrough)，即输入信号是否在输出端出现的标识，取值为0或1;第6个参数表示模块采样周期的个数，S函数支持多采样周期的系统，x0=[为系统初始值设定; flag=1时为S函数被控对象微分方程的描述;flag=3时为S函数输出。仿真结果如图所示。

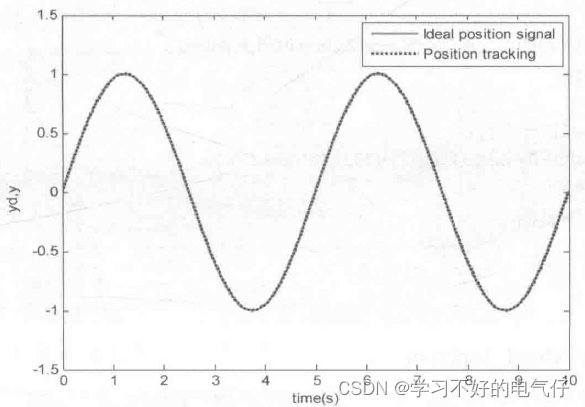
仿真图：

简化的S函数控制器程序：chap1_3ns.m

function [sys,x0]=s_function(t,x,u,flag)

kp=60;

ki=1;

kd=3;

if flag==0

sys=[0,0.1,3,0,1]; %Outputs=1,Inputs=3,DirFeedthrough=0;

x0=[ ];

clseif flag==3

sys(1)=kp*u(1)+ki*u(2)+kd*u(3);

else

sys=[];

end

简化的S函数被控对象程序：chap1_3nplant.m

function [sys,x0]=s_function(t,x,u,flag)

if flag==0

sys=[2,0,1,1,0,0]; %ContStates=2,Outputs=1,Inputs=l

x0=[0.0];

elseif flag==1

sys(1)=x(2)

sys(2)=-(25+10*rands(1))*x(2)+(133+30*rands(1))*u;

elseif flag==3

sys(1)=x(1);

else

sys=[ ];

end

作图程序：chap1_3nplot.m

close all;

plot(t,y(:,1).'r',ty(:,2),'k:','linewidth' ,2);

xlabel( 'time(s)');ylabel('yd,y');

legend('ldeal position signal','Position tracking');