目录
1.栈
1.1栈的概念及结构
1.2栈的实现
1.2.2实现结构的选择
a.数组
b.链表
c.更优的选择
1.2.3实现结构
a.栈的结构体
b.栈的初始化
c.栈的销毁
d.入栈
e.出栈
f.获取栈顶元素
g.获取栈中有效元素个数
h.检测队列是否为空,如果为空返回非零结果,如果非空返回0
2.队列
2.1队列的概念及结构
2.2队列的实现
2.2.1.实现结构的选择
2.2.2.实现结构的选择
a.单个队列节点的结构体
b.维护队列的结构体
c.队列的初始化
d.销毁队列
e.队尾入队列
f.队头出队列
g.获取队列头部元素
h.获取队列队尾元素
i.获取队列中有效元素个数
j.检测队列是否为空,如果为空返回非零结果,如果非空返回0
3.栈和队列面试题
1. 括号匹配问题。OJ链接
2. 用队列实现栈。OJ链接
3. 用栈实现队列。OJ链接
4. 设计循环队列。OJ链接
4.概念选择题
4.1题目
4.2答案
5.附录源码:
5.1栈:
Stack.h
Stack.c
5.2队列
Queue.h
Queue.c
1.栈
1.1栈的概念及结构
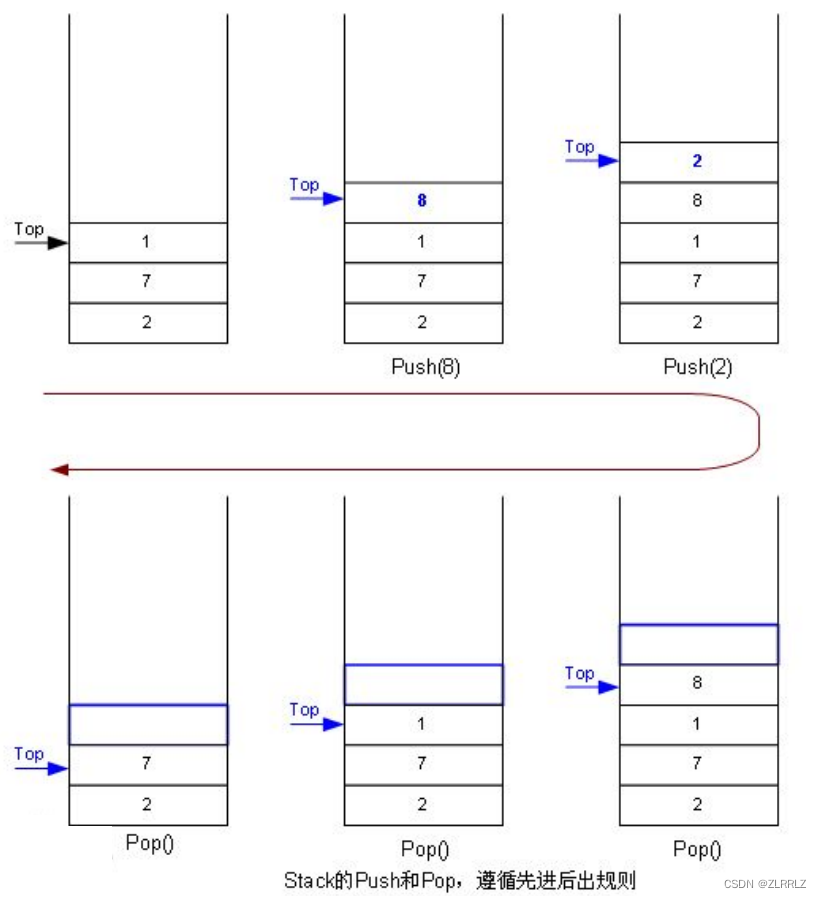
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。

栈在逻辑上仍然是线性的,但是与顺序表、链表不同,栈只能在栈顶入数据,在栈底出数据,不能在任意位置进行操作,栈顶与栈底是根据功能命名的,没有严格规定首部是栈顶,尾部是栈底。
1.2栈的实现
1.2.2实现结构的选择
在数据结构之前的学习中,我们已经学习了链式与数组这两种存储的结构,栈的实现一般都可以使用数组或者链表实现。相对而言数组的结构实现更优一些。因为数组在尾上插入数据的 代价比较小。
a.数组
对于数组而言,如果我们将头部作为栈底,那么压栈出栈就需要挪动许多数据,算法复杂度为较大,因此我们一般将数组头部作为栈顶,尾部作为栈底.

b.链表
与数组不同,对于单链表而言,如果我们将链表的尾部作为栈底,我们是无法直接访问链表尾部的,同时进行压栈、出栈时,我们还需要找到尾节点的前一个节点,这样使用链表构建栈就会相当麻烦,读者读到这里,可能会认为找前一个节点麻烦,这是由于单链表结构的固有缺陷导致的,那我们直接使用双向链表,不就好了吗?确实,找前一个节点不麻烦了,但是为了解决这个问题,使用了双向链表,那么我们每个节点就多出一个需要维护的节点,空间损耗就大了,而且找尾节点还是需要遍历的,总得来说,我们花费的代价就太大了。因此将链表的尾部作为栈底并不是一个明智的选择。因此我们还是使用单链表(不带头),只不过将单链表第一个有效节点处,作为栈顶。这样我们进行压栈、出栈就方便了。
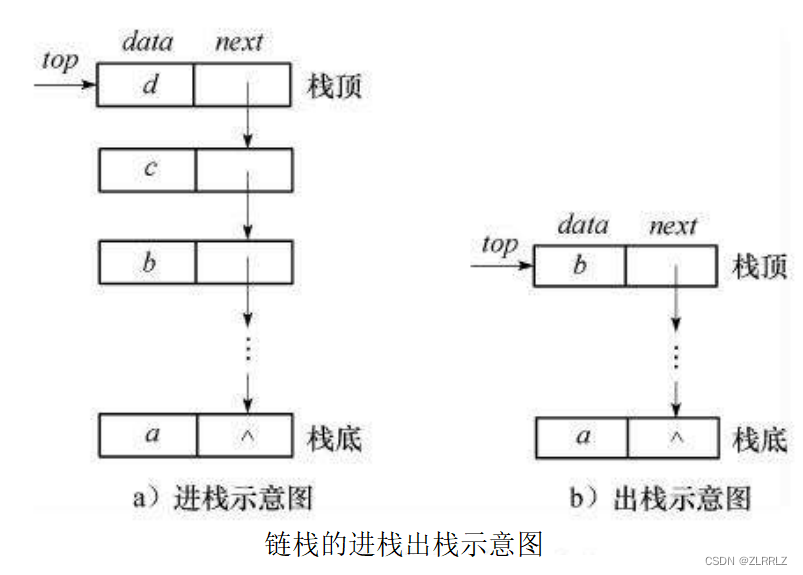
c.更优的选择
数组与链表两种结构看上去各有千秋,不过,实际上有数组去实现栈会更优一些。有的读者可能会认为如果是动态开辟数组的话,不是会有扩容上的消耗吗?同时不是还有将数据迁移到新的空间上的消耗吗?确实,如果仅看这些,按需申请的链表似乎更优一些,但是扩容调用的是系统上的资源,运行很快,并且一次扩容都是按倍扩,扩容的次数并不会很多,更重要的是数组的CPU的高速缓存更好(涉及知识点较多,这里便不展开了),因此,这里笔者主要使用数组来实现栈。
1.2.3实现结构
a.栈的结构体
静态的结构在实践用到的地方并不多,因此我们实现动态增长的栈。栈的结构体中,_a指向动态开辟的数组空间,_top用来指向栈顶元素或者栈顶元素的下一个位置,_capacity用来表示栈的容量
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* _a;
int _top; // 栈顶
int _capacity; // 容量
}Stack;b.栈的初始化
栈的初始化中,需要注意的是_top的初始值初始化为-1与初始化为0是截然不同的。我们的惯性思考会认为没有数据就是0,但是_top此处并不是单纯的表示数据个数的,我们知道数组能访问到最小下表是0,如果_top是表示指向栈顶数据的,那么当_top初始化为0,表示没有数据,当数组内有一个数据时,为了表示有一个数据,我们就将_top+1吗?这样似乎浪费空间了,因此如果_top是表示指向栈顶数据,我们就将_top初始化为-1,如果_top指向栈顶数据的下一个位置,我们就将_top始化为 0,这时的_top就还可以表示表示数组元素的个数了。笔者接下来实现栈的结构,_top指向栈顶元素的下一个位置。
// 初始化栈
void StackInit(Stack* ps)
{
assert(ps);
ps->_a = NULL;
// top指向栈顶数据的下一个位置
ps->_top = 0;
// top指向栈顶数据
//ps->_top = -1;
ps->_capacity = 0;
}c.栈的销毁
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->_a);
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}d.入栈
入栈之前,我们需要先判断数组的空间是否足够,如果不足,我们再扩容,因为_top指向的是栈顶元素的下一个数据,一次插入时的_top当前指向的位置就是要插入数据的位置。之后_top再加一。
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
//扩容
if(ps->_capacity == ps->_top)
{
//对于第一次开辟空间,先初始化4个字节空间,之后每次扩容,扩大两倍
int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
STDataType* newnode = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
if (NULL == newnode)
{
perror("StackInit:realloc");
exit(1);
}
ps->_a = newnode;
//更新容量的记录值
ps->_capacity = newcapacity;
}
ps->_a[ps->_top] = data;
ps->_top++;
}
e.出栈
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
ps->_top--;
}f.获取栈顶元素
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
return ps->_a[ps->_top - 1];
}g.获取栈中有效元素个数
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->_top;
}h.检测队列是否为空,如果为空返回非零结果,如果非空返回0
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->_top == 0;
}2.队列
2.1队列的概念及结构
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出 FIFO(First In First Out) 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头
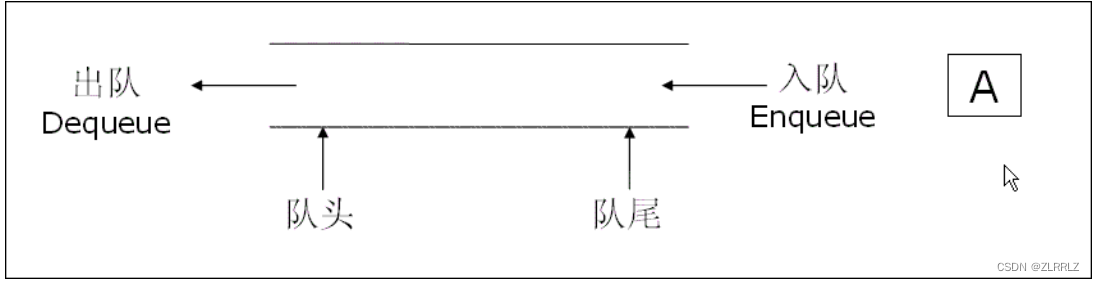
2.2队列的实现
2.2.1.实现结构的选择
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数 组头上出数据时,就需要挪动数据,效率会比较低。
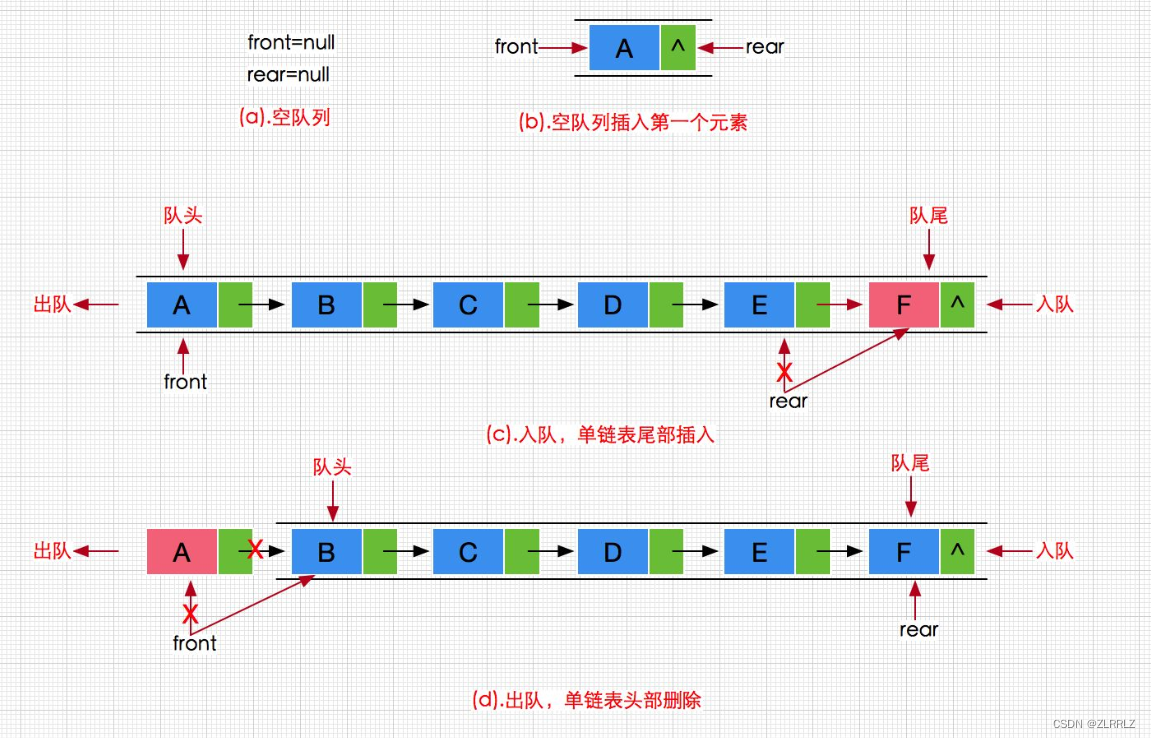
2.2.2.实现结构的选择
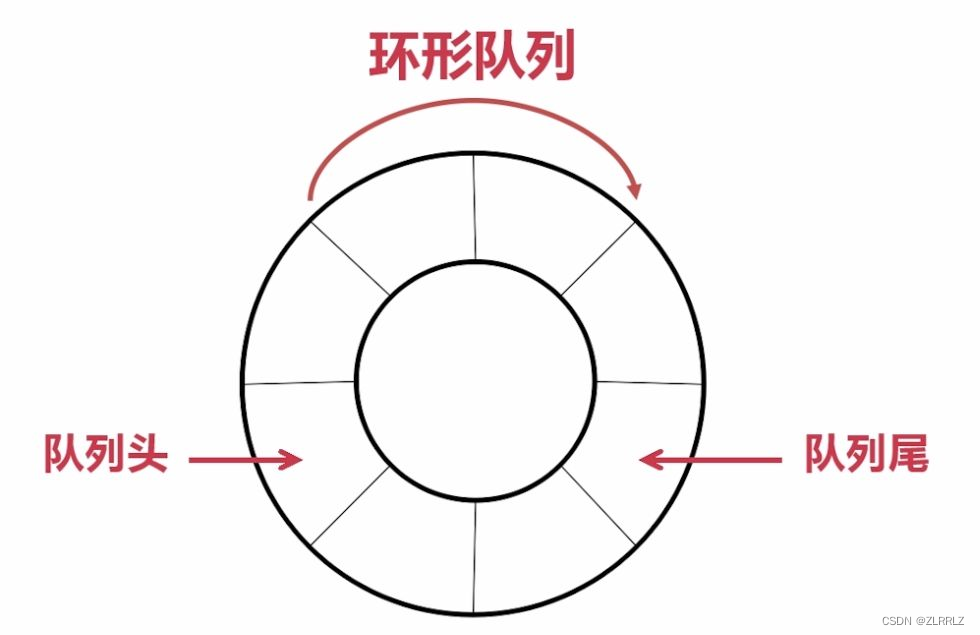
另外扩展了解一下,实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型 时可以就会使用循环队列(涉及到许多其他知识,这里便不过多介绍)。环形队列可以使用数组实现,也可以使用循环链表实现。

a.单个队列节点的结构体
typedef int QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;b.维护队列的结构体
与栈不同,在实现队列时,以入队列为例,我们需要传尾指针,如果要改变尾节点还要传对应的二级指针,同时如果队列现在一个节点都没有,我们还需要传对应头指针的二级指针。总得来说,各种接口的使用似乎非常不便,针对这种问题,我们专门创建一个结构体去维护头指针与尾指针。调用接口时,我们只需要传入这个结构体的指针就可以了。这样我们就可以通过访问结构体来改变对应的头尾指针。此外加上_size记录数据个数


// 队列的结构
typedef struct Queue
{
QNode* _front;
QNode* _rear;
int _size;
}Queue;c.队列的初始化
传入专门维护的结构体初始化。
// 初始化队列
void QueueInit(Queue* q)
{
q->_front = NULL;
q->_rear = NULL;
q->_size = 0;
}d.销毁队列
循环遍历节点,挨个释放
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->_front;
while(cur)
{
QNode* next = cur->_next;
free(cur);
cur = next;
}
q->_front = q->_rear = NULL;
q->_size = 0;
}e.队尾入队列
如果队列内没有节点时,在入队列时,还需要该表头结点。
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (NULL == newnode)
{
perror("QueuePush:malloc failed");
exit(1);
}
newnode->_data = data;
newnode->_next = NULL;
if (NULL == q->_rear)
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
q->_rear = newnode;
}
q->_size++;
}f.队头出队列
出队列之前需要判断是否队列中是否存在数据,没有数据,无法出数据。如果队列队列中只有一个数据,出完数据,还需要改变头结点。
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
assert(q->_size);
QNode* next = q->_front->_next;
free(q->_front);
q->_front = next;
if (q->_size == 1)
{
q->_rear = NULL;
}
q->_size--;
}g.获取队列头部元素
首先判断头指针是否为空,不为空才可以获取头部元素。
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
assert(q->_front);
return q->_front->_data;
}h.获取队列队尾元素
首先判断尾指针是否为空,不为空才可以获取尾部元素。
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
assert(q->_rear);
return q->_rear->_data;
}i.获取队列中有效元素个数
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
return q->_size;
}j.检测队列是否为空,如果为空返回非零结果,如果非空返回0
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q)
{
assert(q);
return q->_size == 0;
}
3.栈和队列面试题
1. 括号匹配问题。OJ链接


这一道题,要求左括号与对应的右括号匹配,当取出字符串中的右括号时,需要与当前右括号的前面第一个左括号括号比对,如果是对应的左括号,则匹配成功,取下一个右括号,并且取前面第一个左括号匹配(已经匹配的左括号不再参与匹配)。我们发现我们总是需要取离右括号最近的左括号(相对其他左括号顺序靠后的元素)。匹配后,已匹配的括号不参加,下次匹配据需向“左找”。
因此根据题意,我们这里可以创建栈,循环遍历字符数组,如果当前是左括号,则入栈,如果是右括号,那么这时,我们就取栈顶的元素(由于栈是后入先出栈,因此栈顶的元素就是左边离右括号最近的左括号),与右括号匹配,如果匹配则,将匹配的左括号出栈,继续循环,如果不匹配,则结束遍历。

#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
#include<stdio.h>
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* _a;
int _top; // 栈顶
int _capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps)
{
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
if(ps->_capacity == ps->_top)
{
int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
STDataType* newnode = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
if (NULL == newnode)
{
perror("StackInit:realloc");
exit(1);
}
ps->_a = newnode;
ps->_capacity = newcapacity;
}
ps->_a[ps->_top] = data;
ps->_top++;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
ps->_top--;
}
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->_top;
}
// 检测栈是否为空,如果为空返回0,如果不为空返回非零结果
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->_top;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->_a);
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
bool isValid(char* s)
{
Stack p;
StackInit(&p);
while(*s)
{
if(*s == '(' || *s == '{' || *s == '[')//左括号入栈
{
StackPush(&p,*s);
}
else
{
if(!StackEmpty(&p))//右括号入栈前不能没有左括号,否则一定会出现不匹配的情况
{
StackDestroy(&p);
return false;
}
char top = 0;
top = StackTop(&p);
if(top == '(' && *s != ')'||top == '{' && *s != '}'||top == '[' && *s != ']')//括号不匹配返回false
{
StackDestroy(&p);
return false;
}
StackPop(&p);//匹配成功,将匹配的左括号出栈
}
s++;//移动到下一个括号
}
int ret = !StackEmpty(&p);//判断栈内是否为空,为空说明存在未匹配的左括号
StackDestroy(&p);
return ret;
}2. 用队列实现栈。OJ链接

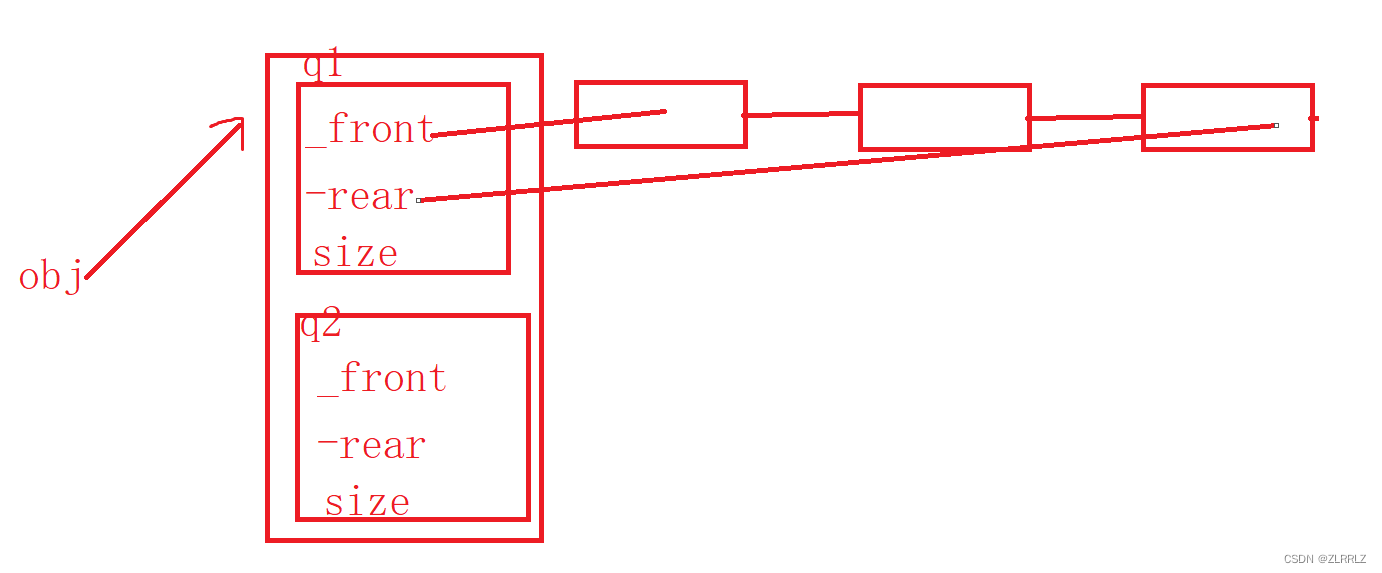
这一题,我们需要根据队列先进先出的性质实现栈后进先出的性质,题目给了我们两个队列,因此这题就是通过将数据在两个列类之间转移来完成的,问题的关键就在于如何转移数据。

如果说队列中已经有数据,为了出4,这是我们就可以将1、2、3入队列入到q2中,这时我们就可以出q1中的4,达到后进先出的效果,之后加入我们入栈5,6呢?我们又将5,6入到哪个队列中呢?

假如们入到 q1,中,这时如果我们将5入到q2,再出6,似乎没什么问题,那么这是如果我们不出6,我们还需要继续导入数据呢?

这是我们发现,面对两个都不为空的队列,我们再想入数据,我们必须先遍历已经存储的数据进行,判断当数据较多时,我们就会发现复杂度以及程序的逻辑性都不会太好。因此,为了避免这一混乱的情况发生,我们必须保证将数据入到不为空的队列,这样出数据将数据导到空队列中,出完数量后,就又保持两队列一空一不为空了。
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include"stdbool.h"
typedef int QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* _front;
QNode* _rear;
int _size;
}Queue;
void QueueInit(Queue* q)
{
q->_front = NULL;
q->_rear = NULL;
q->_size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (NULL == newnode)
{
perror("QueuePush:malloc failed");
exit(1);
}
newnode->_data = data;
newnode->_next = NULL;
if (0 == q->_size)
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
q->_rear = q->_rear->_next;
}
q->_size++;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
assert(q->_size);
QNode* next = q->_front->_next;
free(q->_front);
q->_front = next;
if (q->_size == 1)
{
q->_rear = NULL;
}
q->_size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
assert(q->_size);
return q->_front->_data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
assert(q->_size);
return q->_rear->_data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
return q->_size;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q)
{
assert(q);
return q->_size == 0;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->_front;
while(cur)
{
QNode* next = cur->_next;
free(cur);
cur = next;
}
q->_front = q->_rear = NULL;
q->_size = 0;
}
typedef struct {
Queue q1;
Queue q2;
} MyStack;
MyStack* myStackCreate() {
MyStack*pst = (MyStack*)malloc(sizeof(MyStack));
//创建模拟的栈时,只能malloc动态创建,不能静态开辟,否则出了函数,开辟空间会被收回
//也不能使用static, 否则多次调用函数,值会一直保存,会出问题。
if(NULL == pst)
{
perror("malloc");
exit(1);
}
QueueInit(&pst->q1);
QueueInit(&pst->q2);
return pst;
}
void myStackPush(MyStack* obj, int x) {
if(!QueueEmpty(&obj->q1))
{
QueuePush(&obj->q1,x);
}
else
{
QueuePush(&obj->q2,x);
}
}
int myStackPop(MyStack* obj) {
//假设法
Queue* empty = &(obj->q1);
Queue* nonempty = &(obj->q2);
if(!QueueEmpty(&(obj->q1)))
{
nonempty = &(obj->q1);
empty = &(obj->q2);
}
//不为空的队列前size-1导走,删除最后一个就是栈顶数据
while(QueueSize(nonempty) > 1)
{
QueuePush(empty,QueueFront(nonempty));
QueuePop(nonempty);
}
int top = QueueFront(nonempty);
QueuePop(nonempty);
return top;
}
int myStackTop(MyStack* obj) {
if(!QueueEmpty(&(obj->q1)))
{
return QueueBack(&(obj->q1));
}
else
{
return QueueBack(&(obj->q2));
}
}
bool myStackEmpty(MyStack* obj) {
//两个队列都为空才是空
return QueueEmpty(&(obj->q1))&&QueueEmpty(&(obj->q2));
}
void myStackFree(MyStack* obj) {
QueueDestroy(&(obj->q1));
QueueDestroy(&(obj->q2));
free(obj);
}
/**
* Your MyStack struct will be instantiated and called as such:
* MyStack* obj = myStackCreate();
* myStackPush(obj, x);
* int param_2 = myStackPop(obj);
* int param_3 = myStackTop(obj);
* bool param_4 = myStackEmpty(obj);
* myStackFree(obj);
*/
需要注意的是最后销毁时,要先销毁队列对应的空间,在销毁存储两个队列指针的空间。
3. 用栈实现队列。OJ链接

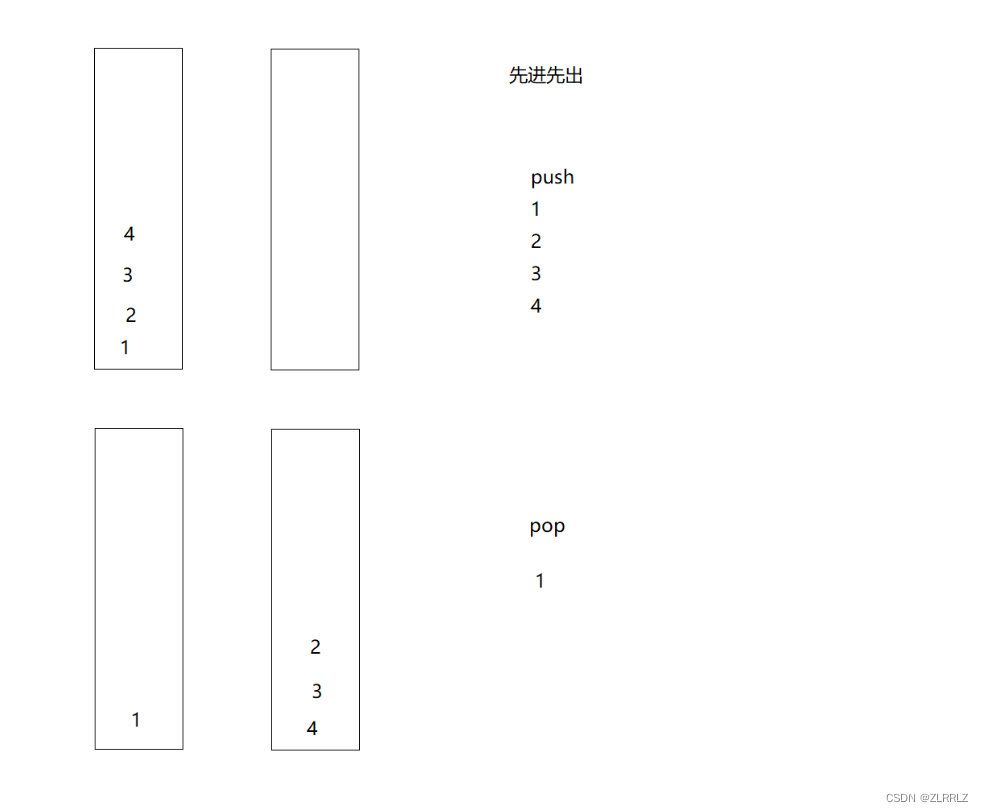
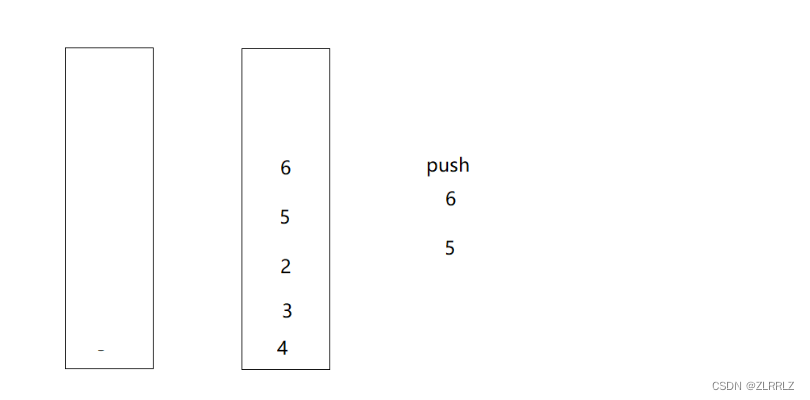
对于这一题,如果我们沿用用队列实现栈的思路,似乎也可以,我们将先将其他数据入到另一个栈中,再留下要出栈的数据出栈。但是我们要入栈时,我们不能在入到非空的栈中,因为这样,出数据的时候,顺序就完全乱了,对此,我们可以将原数据再倒回原数据中,再向非空栈中入数据。这样就没问题了,但是这样就比较麻烦了。

根据观察,我们发现其实在将数据到到空栈是,原数据顺序会倒过来,这是我们再出栈,就直接实现了先进先出的效果。
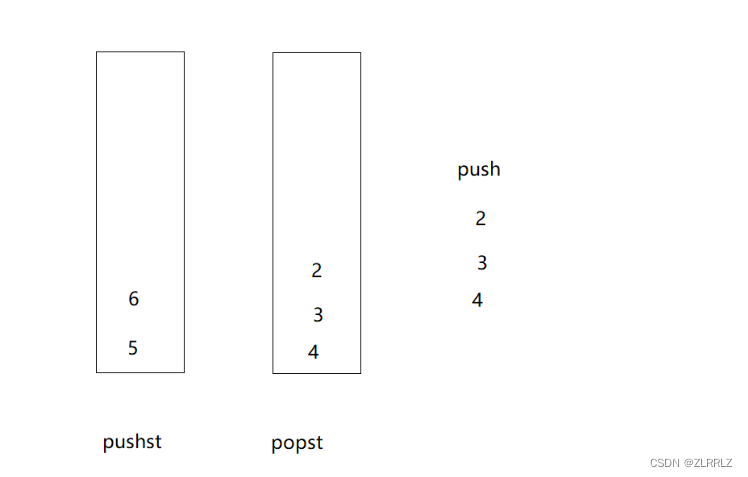
因此我们将两个栈分成一个专门出数据,一个专门入数据,当出数据栈popst为空,我们就将入数据栈pushst数据全部导到popst中(必须一次性将所有数据全部导入,否则顺序就乱了。)入数据时,直接往对应栈入就行了。

#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
#include<stdio.h>
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* _a;
int _top; // 栈顶
int _capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps)
{
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
if(ps->_capacity == ps->_top)
{
int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
STDataType* newnode = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
if (NULL == newnode)
{
perror("StackInit:realloc");
exit(1);
}
ps->_a = newnode;
ps->_capacity = newcapacity;
}
ps->_a[ps->_top] = data;
ps->_top++;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
ps->_top--;
}
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->_top;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->_top == 0;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->_a);
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
typedef struct {
Stack pushst;
Stack popst;
} MyQueue;
MyQueue* myQueueCreate() {
MyQueue* q1 = (MyQueue*)malloc(sizeof(MyQueue));
StackInit(&q1->pushst);
StackInit(&q1->popst);
return q1;
}
void myQueuePush(MyQueue* obj, int x) {
//实现入队列数据
StackPush(&obj->pushst,x);
}
int myQueuePeek(MyQueue* obj) {
if(StackEmpty(&obj->popst))
{
//倒数据
//实现出队列数据
while(!StackEmpty(&obj->pushst))//专门出数据的栈为空,就先导入一下数据
{
StackPush(&obj->popst,StackTop(&obj->pushst));
StackPop(&obj->pushst);
}
}
return StackTop(&obj->popst);
}
int myQueuePop(MyQueue* obj) {
//出队列队头数据
int front = myQueuePeek(obj);
StackPop(&obj->popst);
return front;
}
bool myQueueEmpty(MyQueue* obj) {
//两个栈都为空,队列才为空
return StackEmpty(&obj->pushst)&&StackEmpty(&obj->popst);
}
void myQueueFree(MyQueue* obj) {
//先释放对应栈空间,再释放队列对应空间
StackDestroy(&obj->pushst);
StackDestroy(&obj->popst);
free(obj);
}
/**
* Your MyQueue struct will be instantiated and called as such:
* MyQueue* obj = myQueueCreate();
* myQueuePush(obj, x);
* int param_2 = myQueuePop(obj);
* int param_3 = myQueuePeek(obj);
* bool param_4 = myQueueEmpty(obj);
* myQueueFree(obj);
*/4. 设计循环队列。OJ链接

这道题目的意思就是队列的的空间大小是固定的,这些空间可以重复使用,看到这一题的循环结构,也许有的读者会想到链表,认为链表的结构完成这一题会比数组简单,但是实际上并不是这样的,笔者这里先以数组完成这题,链表的不便后文讲解。
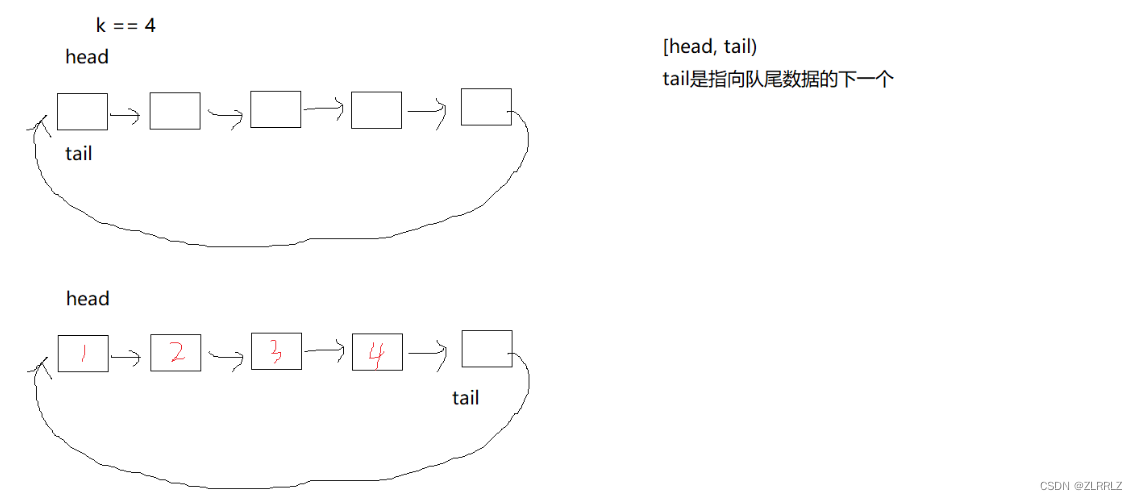
首先假设要插入的空间K是4,这是如果我们开辟4个空间,head、tail都初始化为0,push一个数据,tail++,pop一个数据,head++,当tail、head值大于K,通过%K,实现回环,这样head == tail时,就代表数组为空的情况了,但是,我们发现如果数组满时也会出现head == tail,这就是我们说的假溢出的情况了。

为了解决这个问题,笔者有两种方法,一种是创建size专门记录数组元素个数;还有一种是多开一个空间。笔者接下来重点介绍第二种(对于这类问题一些官方解答更喜欢用第二种方法)。
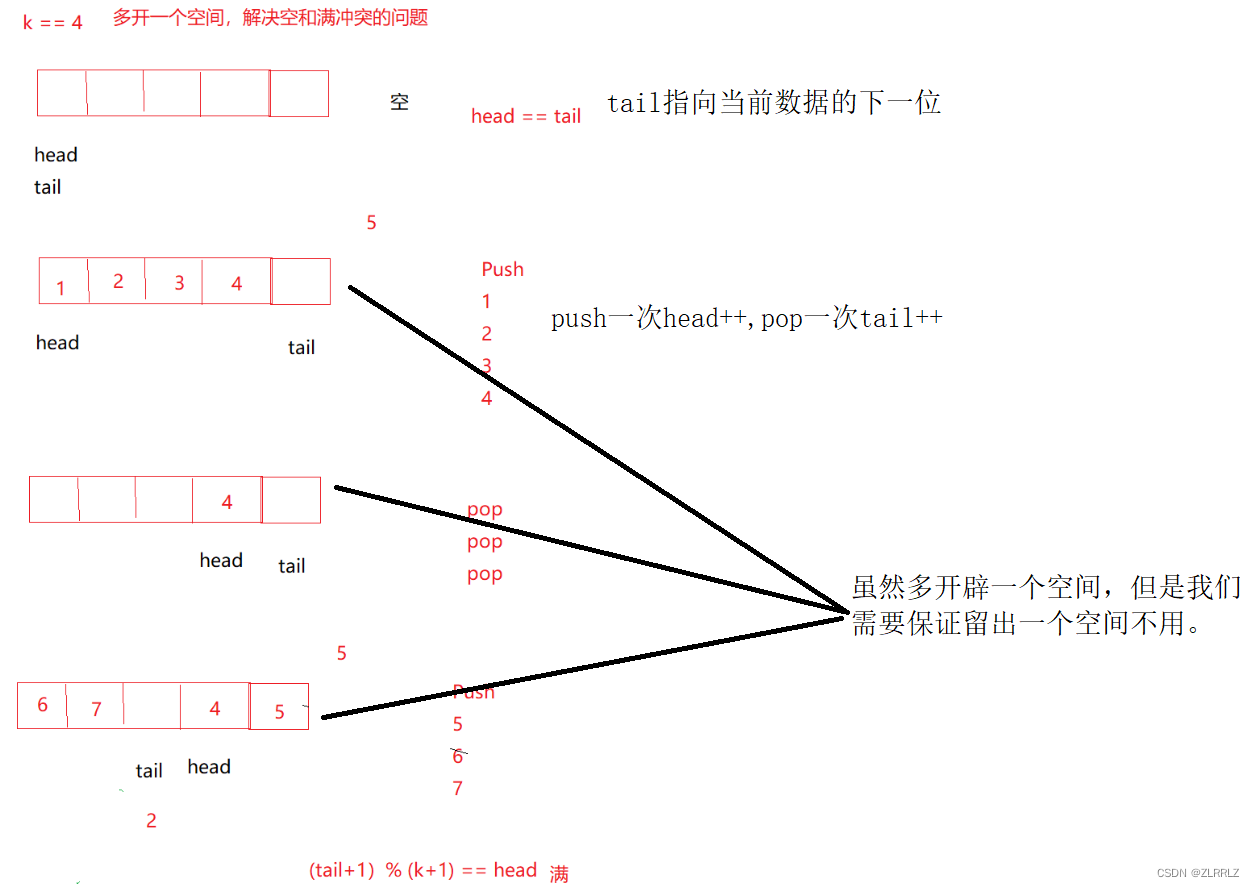
如上图,其他不变,只是我们判断数组满到条件变成了(tail+1)%(k+1) == head;这是为什么呢?我们知道,head是指向队列的头,tail指向尾的下一位,因为我们多开了一个空间,并且是按序的空出空间,因此,当数组满时,尾的空间后面就是空空间,tail指向它,这时如果tail再向前走一步,就与head相等,不过这时,为了避免出现越界的情况,tail+1需要%(K+1),这就相当于tail+1>5时,tail+1-5,tail回到数组开头,同时数组越界的情况是相对与数组总长的,因此这里是%(k+1)不是%k.

typedef struct {//创建结构体存储需要用到的值方便维护
int k;
int head;
int tail;
int* a;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {//初始化结构体
MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
obj->a = (int*)malloc((k + 1) * sizeof(int));
obj->head = 0;
obj->tail = 0;
obj->k = k;
return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->head == obj->tail;//head == tail为空
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->tail + 1)%(obj->k + 1) == obj->head;//(tail + 1)%(k + 1) == head 为满
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(myCircularQueueIsFull(obj))
{
return false;
}
else
{
obj->a[obj->tail] = value;
obj->tail = (obj->tail + 1) % (obj->k + 1);//防止越界
return true;
}
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return false;
}
obj->head = (obj->head + 1) % (obj->k + 1);//防止head越界
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))//为空取不到队头的数据
{
return -1;
}
else
{
return obj->a[obj->head];
}
}
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))//为空取不到队尾的数据
{
return -1;
}
else
{
return obj->a[(obj->tail-1 + obj->k + 1) % (obj->k + 1)];
}
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
free(obj);
}
/**
* Your MyCircularQueue struct will be instantiated and called as such:
* MyCircularQueue* obj = myCircularQueueCreate(k);
* bool param_1 = myCircularQueueEnQueue(obj, value);
* bool param_2 = myCircularQueueDeQueue(obj);
* int param_3 = myCircularQueueFront(obj);
* int param_4 = myCircularQueueRear(obj);
* bool param_5 = myCircularQueueIsEmpty(obj);
* bool param_6 = myCircularQueueIsFull(obj);
* myCircularQueueFree(obj);
*/这里需要特别注意的是,当我们取队尾的数据时,由于tail是指向队尾数据的下一位,因此如果tail在数组头,tail-1取队尾就会出现负数的情况,因此与(tail+1)%(k+1)类似,我们要将(tail+1 +k+1)%(k+1),这样就可以避免出现,负数的情况,如果tail不在队头这样处理也不会有问题。
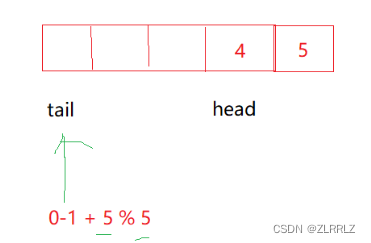
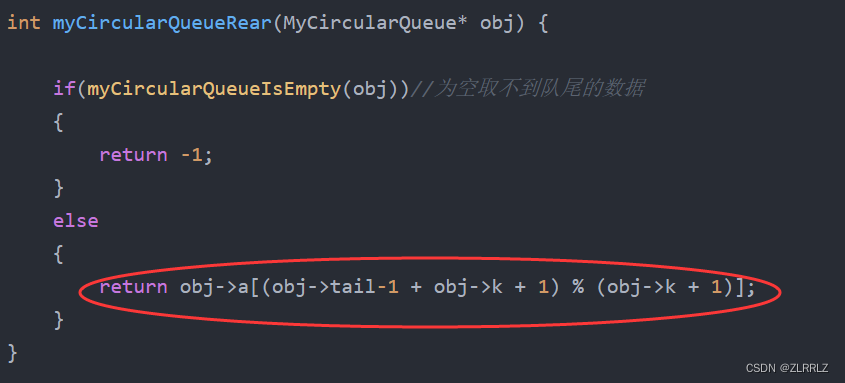
那么回到一开始的问题,为什么笔者说,使用链表不像看上去那样简单呢?首先,用链表形成循环队列,不像数组那样直接申请一块空间方便,其次由于tail是指向尾的下一个位置,因此我们如果想要找尾会很麻烦,对此可以使用双向链表、遍历寻找尾、专门创建变量记录tail前一个节点,总的来说,使用链表不光没有什么实质的好处,反而还会有不少麻烦。当然,如果读者想要用链表完成,也不无不可。
4.概念选择题
4.1题目
1.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈,然后再依次出栈,则元素出栈的顺序是( )。
A 12345ABCDE
B EDCBA54321
C ABCDE12345
D 54321EDCBA
2.若进栈序列为 1,2,3,4 ,进栈过程中可以出栈,则下列不可能的一个出栈序列是()
A 1,4,3,2
B 2,3,4,1
C 3,1,4,2
D 3,4,2,1
3.循环队列的存储空间为 Q(1:100) ,初始状态为 front=rear=100 。经过一系列正常的入队与退队操作 后, front=rear=99 ,则循环队列中的元素个数为( )
A 1
B 2
C 99
D 0或者100
4.以下( )不是队列的基本运算?
A 从队尾插入一个新元素
B 从队列中删除第i个元素
C 判断一个队列是否为空
D 读取队头元素的值
5.现有一循环队列,其队头指针为front,队尾指针为rear;循环队列长度为N。其队内有效长度为?(假设 队头不存放数据)
A (rear - front + N) % N + 1
B (rear - front + N) % N
C ear - front) % (N + 1)
D (rear - front + N) % (N - 1)
4.2答案
1.B //依次入栈,入完再出栈,后入先出
2.C //不可能出现2不出,就出到1
3.D //属于没有多开一个空间的方法,相等时可能为空,可能满。
4.B
5.B
5.附录源码:
5.1栈:
Stack.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
#include<stdio.h>
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* _a;
int _top; // 栈顶
int _capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps);
// 入栈
void StackPush(Stack* ps, STDataType data);
// 出栈
void StackPop(Stack* ps);
// 获取栈顶元素
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数
int StackSize(Stack* ps);
// 检测栈是否为空,如果为空返回0 ,如果不为空返回非零结果
bool StackEmpty(Stack* ps);
// 销毁栈
void StackDestroy(Stack* ps);
Stack.c
#include"Stack.h"
// 初始化栈
void StackInit(Stack* ps)
{
assert(ps);
ps->_a = NULL;
// top指向栈顶数据的下一个位置
ps->_top = 0;
// top指向栈顶数据
//ps->_top = -1;
ps->_capacity = 0;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
//扩容
if(ps->_capacity == ps->_top)
{
int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
STDataType* newnode = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
if (NULL == newnode)
{
perror("StackInit:realloc");
exit(1);
}
ps->_a = newnode;
ps->_capacity = newcapacity;
}
ps->_a[ps->_top] = data;
ps->_top++;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
ps->_top--;
}
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->_top > 0);
return ps->_a[ps->_top - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->_top;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool StackEmpty(Stack* ps)
{
assert(ps);
return ps->_top == 0;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->_a);
ps->_a = NULL;
ps->_capacity = ps->_top = 0;
}
5.2队列
Queue.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include"stdbool.h"
typedef int QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* _front;
QNode* _rear;
int _size;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);
Queue.c
#include"queue.h"
// 初始化队列
void QueueInit(Queue* q)
{
q->_front = NULL;
q->_rear = NULL;
q->_size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (NULL == newnode)
{
perror("QueuePush:malloc failed");
exit(1);
}
newnode->_data = data;
newnode->_next = NULL;
if (NULL == q->_rear)
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
q->_rear = newnode;
}
q->_size++;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
assert(q->_size);
QNode* next = q->_front->_next;
free(q->_front);
q->_front = next;
if (q->_size == 1)
{
q->_rear = NULL;
}
q->_size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
assert(q->_front);
return q->_front->_data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
assert(q->_rear);
return q->_rear->_data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
return q->_size;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Queue* q)
{
assert(q);
return q->_size == 0;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->_front;
while(cur)
{
QNode* next = cur->_next;
free(cur);
cur = next;
}
q->_front = q->_rear = NULL;
q->_size = 0;
}

![[初始计算机]——计算机网络的基本概念和发展史及OSI参考模型](https://img-blog.csdnimg.cn/direct/7d997e4e47c8413293e563cb4d7c2841.png)







![[图的搜索]5.图解狄克斯特拉算法及其代码演示](https://img-blog.csdnimg.cn/direct/f93a9eca90f2439aa7b11804b68239bb.png)


